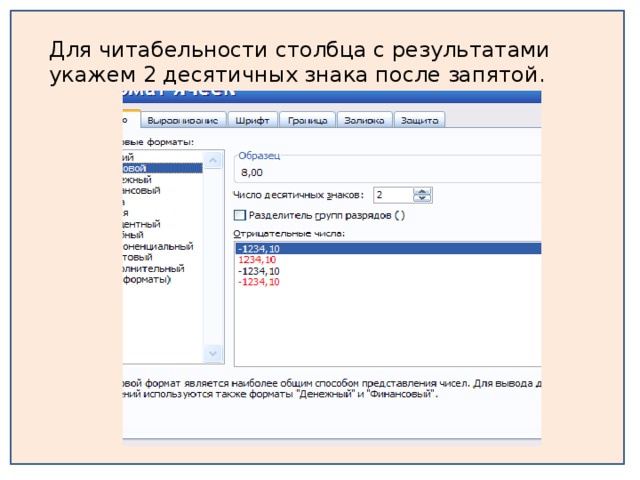
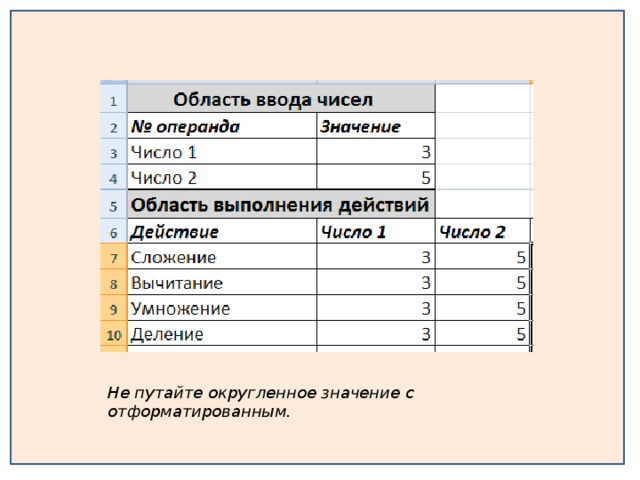
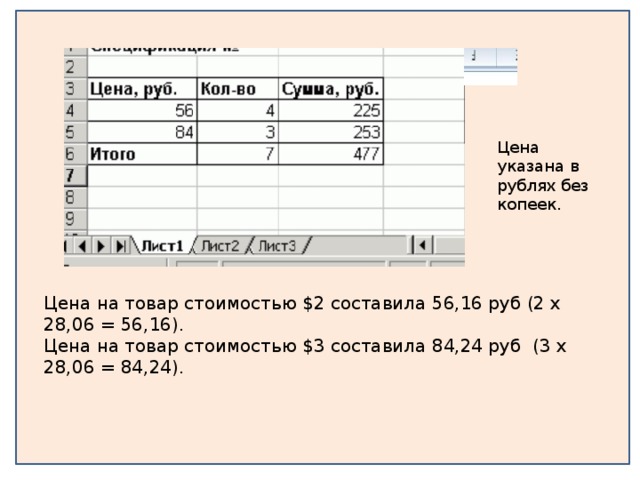
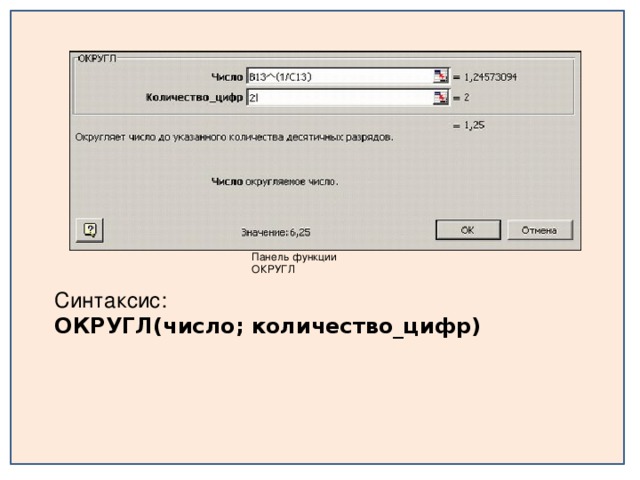
Просмотр содержимого презентации
«Математическая модель оптимизационной задачи»

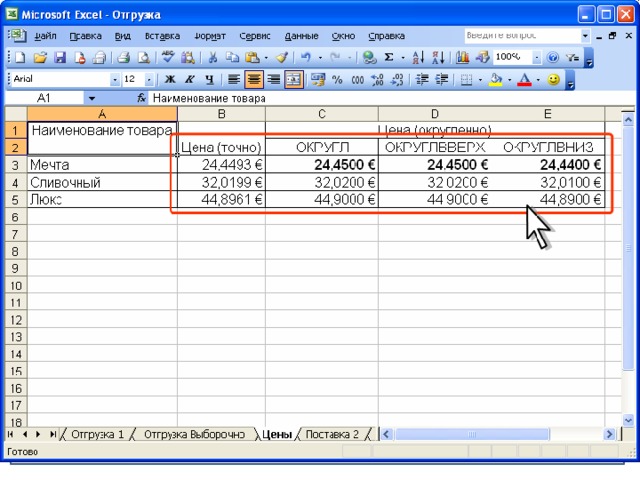
Математическая модель оптимизационной задачи. Решение оптимизационных задач с помощью Excel

Актуализация знаний:
- Какие задачи называются оптимизационными ?
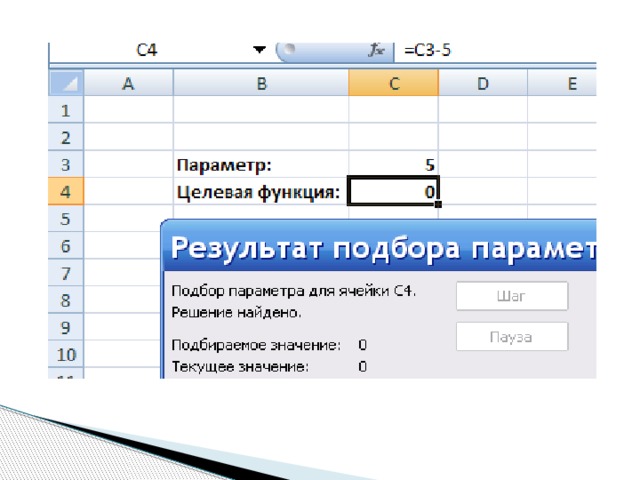
- С помощью каких средств в Excel можно решать оптимизационные задачи? Подбор параметра. Поиск решения. Какие команды нужно выполнить, чтобы воспользоваться средством « Подбор параметра »? Данные – «Анализ что-если» – Подбор параметра. Какие команды нужно выполнить, чтобы воспользоваться средством « Поиск решения »? Данные – Поиск решения.
- С помощью каких средств в Excel можно решать оптимизационные задачи?
- Подбор параметра. Поиск решения.
- Какие команды нужно выполнить, чтобы воспользоваться средством « Подбор параметра »?
- Данные – «Анализ что-если» – Подбор параметра.
- Какие команды нужно выполнить, чтобы воспользоваться средством « Поиск решения »?
- Данные – Поиск решения.

Математическая модель – это математическое представление реальности.

Построение математической модели оптимизационной задачи:
- переменные – неизвестные величины, значения которых нужно найти в результате решения задачи;
- целевая функция – величина, которая зависит от переменных и значения которой необходимо максимизировать или минимизировать;
- критерий – условие минимизации или максимизации целевой функции;
- ограничения – условия, которым должны удовлетворять переменные.

Решение задачи линейного программирования
Фирменные блюда

Задача: Фирменные блюда
Необходимо приготовить фирменные блюда трех видов, используя ингредиенты четырех видов при известной норме использования ингредиентов (гр) для приготовления одной порции каждого блюда.
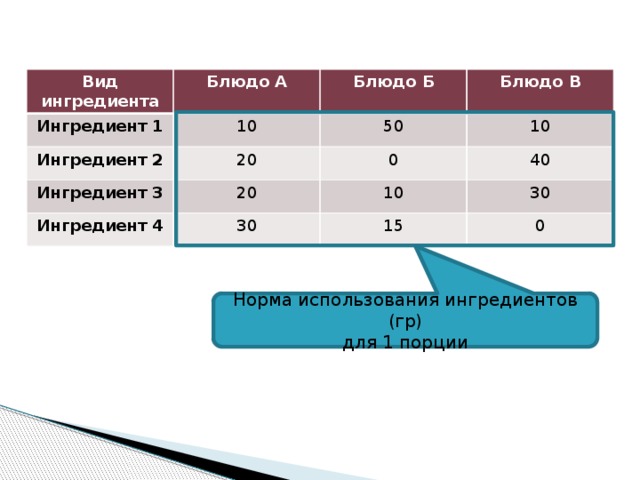
Вид ингредиента
Ингредиент 1
Блюдо А
Блюдо Б
10
Ингредиент 2
Блюдо В
50
20
Ингредиент 3
Ингредиент 4
10
0
20
30
40
10
30
15
0
Норма использования ингредиентов (гр)
для 1 порции

Стоимость одной порции
- Блюдо А – 120 грн;
- Блюдо Б – 100 грн;
- Блюдо В – 80 грн.

Ежедневная доставка в заведение ингредиентов:
- Ингредиент 1 – 5 кг;
- Ингредиент 2 – 4 кг;
- Ингредиент 3 – 4 кг;
- Ингредиент 4 – 3 кг;

?
Определить, какое количество порций каждого из фирменных блюд следует приготовить, чтобы общая стоимость блюд была максимальной ?
?
?
?

Построение математической модели
- Х 1 – количество порций блюда А .
- Х 2 – количество порций блюда Б .
- Х 3 – количество порций блюда В .
- Общую стоимость блюд можно определить по формуле:
120Х 1 + 100 Х 2 + 80 Х 3 – формула целевой функции
 =0 , Х 2 =0 , Х 3 =0 (кол-во порций – неотрицательные числа) (10) Х 1 , Х 2 , Х 3 – целые числа" width="640"
=0 , Х 2 =0 , Х 3 =0 (кол-во порций – неотрицательные числа) (10) Х 1 , Х 2 , Х 3 – целые числа" width="640"
Модель задачи:
(4) 120Х 1 + 100 Х 2 + 80 Х 3 max (целевая функция)
(5) 10Х 1 + 50 Х 2 + 10 Х 3 (затраты ингр.1)
(6) 20Х 1 + 40 Х 3 (затраты ингр.2)
(7) 20Х 1 + 10 Х 2 + 30 Х 3 (затраты ингр.3)
(8) 30Х 1 + 15 Х 2 (затраты ингр.4)
(9) Х 1 =0 , Х 2 =0 , Х 3 =0 (кол-во порций – неотрицательные числа)
(10) Х 1 , Х 2 , Х 3 – целые числа
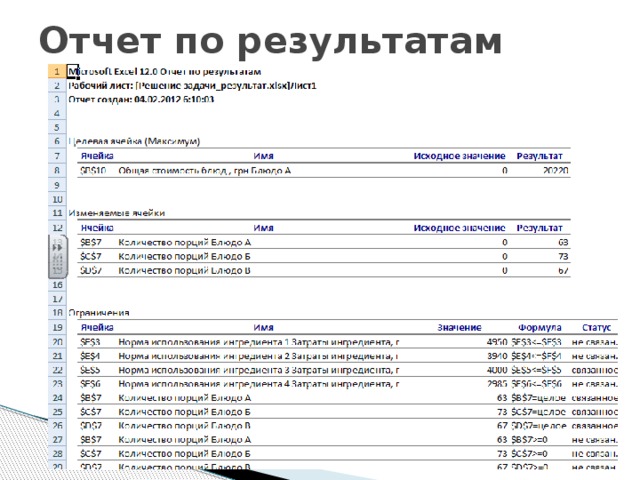
Отчет по результатам

Домашнее задание:
Просмотр содержимого презентации
«Основы корреляционного анализа»

Основы корреляционного анализа
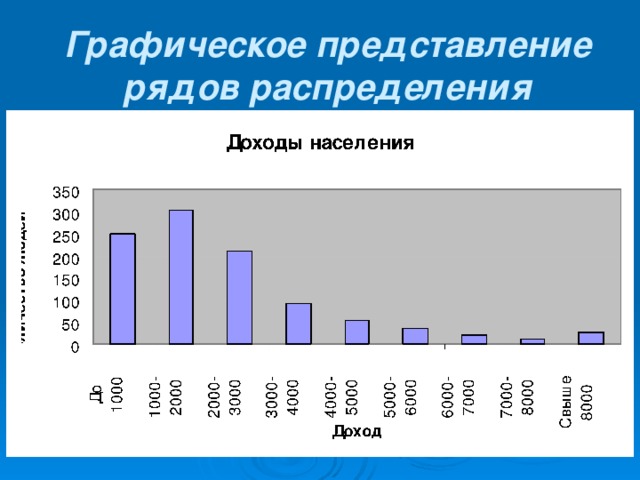
Графическое представление рядов распределения

Пример дискретного ряда распределения
Число на игровой кости
1
Количество
2
выпадений
50
3
43
4
51
5
47
6
39
53

Более точные исследования зависимостей между двумя или большим количеством выборок является задачей специальных разделов математической статистики корреляционного и регрессионного анализа

Корреляционный анализ дает возможность установить, существует ли связь между явлениями и насколько она сильна. Если связь окажется существенной, то целесообразно воспользоваться методами регрессионного анализа , основная задача которого состоит в определении характера связи и построении ее математической модели.

Факторные признаки являются такими, что от них зависят другие. Результативные признаки сами зависят от других признаков.

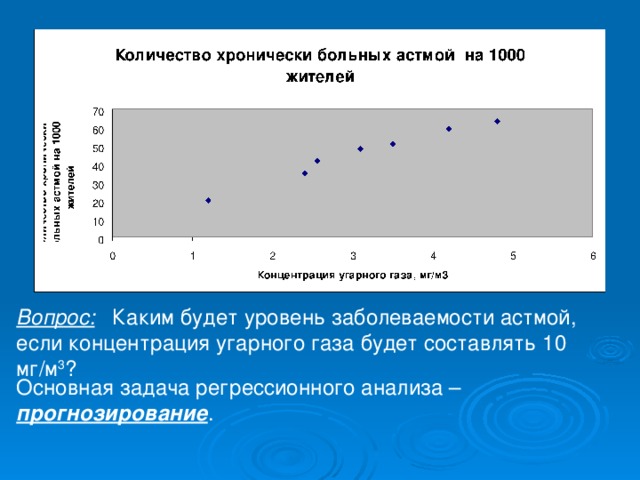
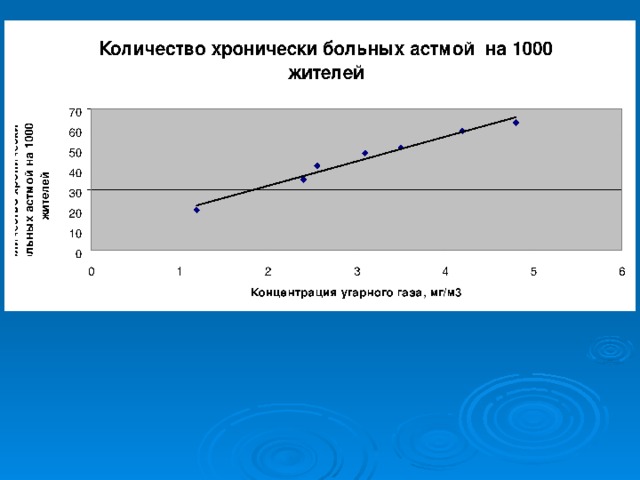
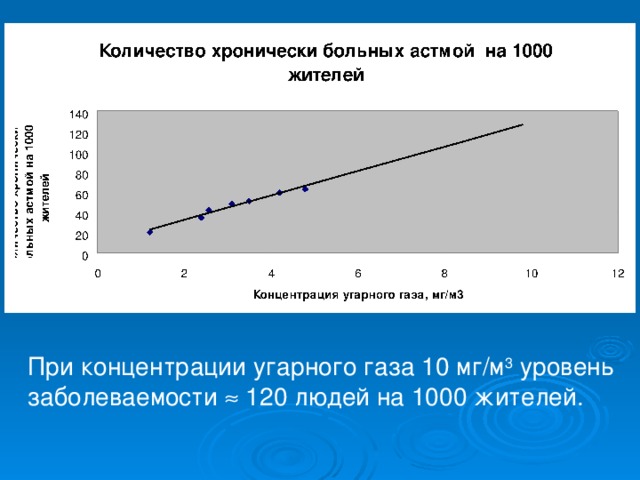
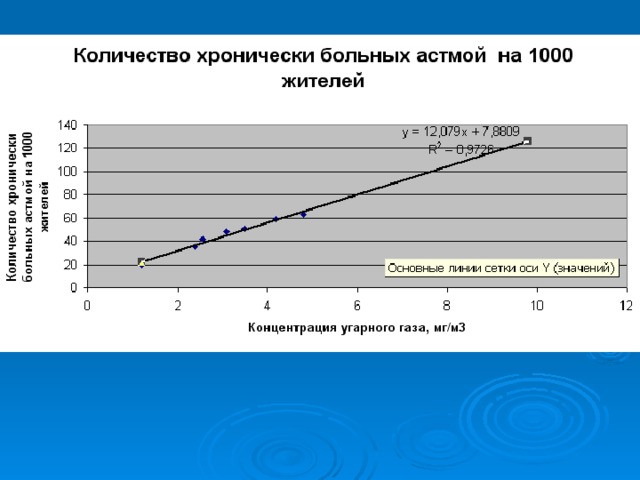
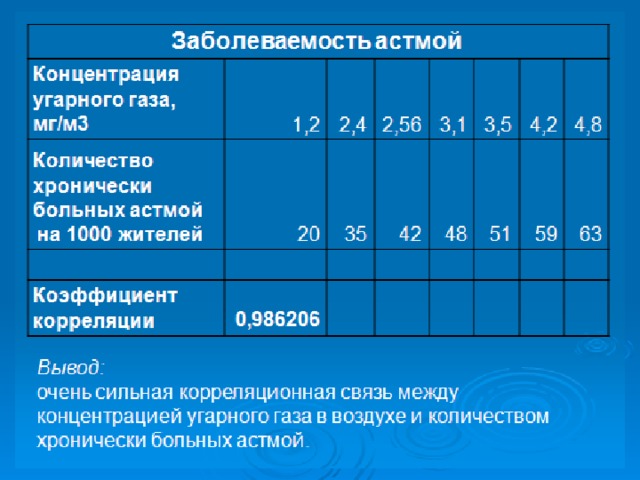
Пример: Заболеваемость астмой
Концентрация угарного газа, мг/м3
Количество хронически больных астмой на 1000 жителей
1,20
20
2,40
2,56
35
42
3,10
3,50
48
51
4,20
4,80
59
63

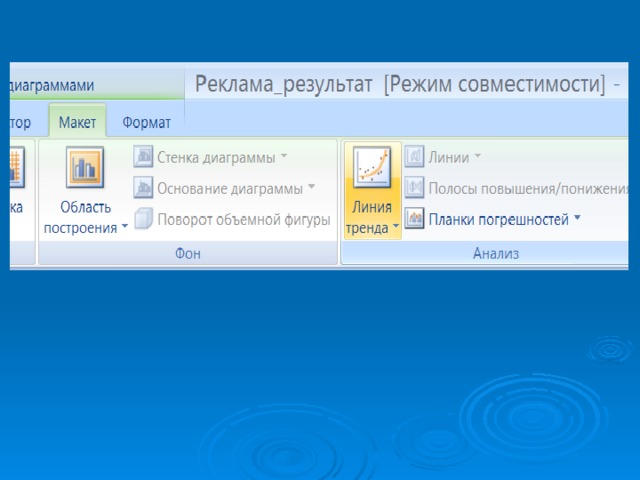
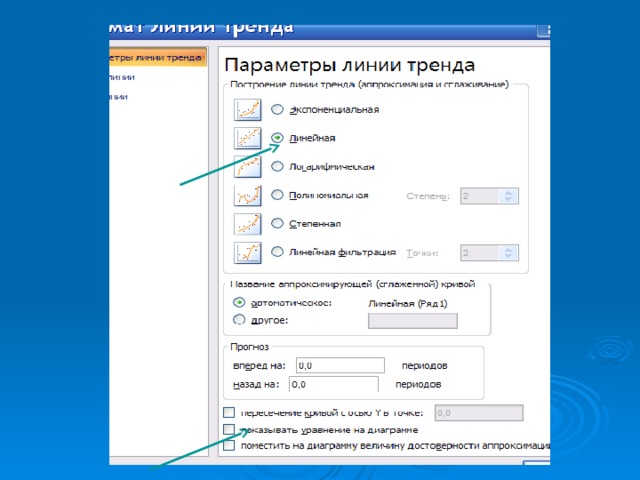
Графический анализ корреляционной связи
Линия тренда
Диаграмма рассеивания
Факторный признак
Результативный признак
Пример прямой корреляционной связи
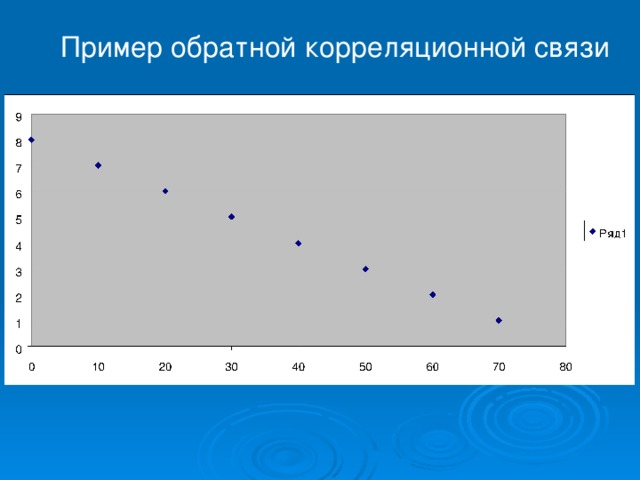
Пример обратной корреляционной связи
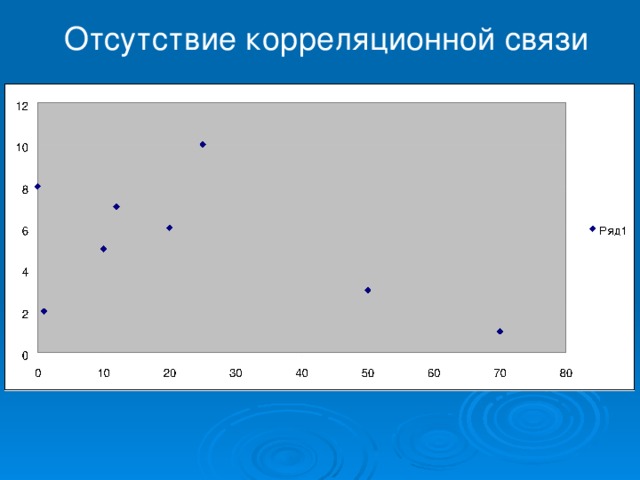
Отсутствие корреляционной связи
![Коэффициент корреляции Качество связи между двумя величинами можно выразить с помощью коэффициента корреляции . Это число k из интервала [-1;1]. Если k близко к -1, то корреляционная связь между величинами является обратной , а если k близко к 1 – прямой . Чем ближе k к нулю, тем корреляционная связь слабее. Если говорить более основательно, то прочность линейной корреляционной связи оценивается так: |k| 0,8 – сильная корреляционная связь; 0,4 |k| |k| < 0,4 – корреляционная связь отсутствует.](https://fhd.multiurok.ru/f/c/e/fce8e5516d1b51bc7c7e62257c78ba00aed8a43a/img_Rasshirennyy_kurs_Excel_1416977721_60805_1_10.jpg)
Коэффициент корреляции
Качество связи между двумя величинами можно выразить с помощью коэффициента корреляции . Это число k из интервала [-1;1]. Если k близко к -1, то корреляционная связь между величинами является обратной , а если k близко к 1 – прямой . Чем ближе k к нулю, тем корреляционная связь слабее. Если говорить более основательно, то прочность линейной корреляционной связи оценивается так:
|k| 0,8 – сильная корреляционная связь;
0,4 |k|
|k|

В МS Excel для вычисления коэффициента корреляции используется функция КОРРЕЛ : КОРРЕЛ(диапазон_1; диапазон_2) , где диапазон_1 диапазон_2 содержат наборы значений, между которыми определяется зависимость.
Просмотр содержимого презентации
«Подбор параметра»
Просмотр содержимого презентации
«Регрессионный анализ»
Просмотр содержимого презентации
«Точность и разрядность результатов»
















 =0 , Х 2 =0 , Х 3 =0 (кол-во порций – неотрицательные числа) (10) Х 1 , Х 2 , Х 3 – целые числа" width="640"
=0 , Х 2 =0 , Х 3 =0 (кол-во порций – неотрицательные числа) (10) Х 1 , Х 2 , Х 3 – целые числа" width="640"












![Коэффициент корреляции Качество связи между двумя величинами можно выразить с помощью коэффициента корреляции . Это число k из интервала [-1;1]. Если k близко к -1, то корреляционная связь между величинами является обратной , а если k близко к 1 – прямой . Чем ближе k к нулю, тем корреляционная связь слабее. Если говорить более основательно, то прочность линейной корреляционной связи оценивается так: |k| 0,8 – сильная корреляционная связь; 0,4 |k| |k| < 0,4 – корреляционная связь отсутствует.](https://fhd.multiurok.ru/f/c/e/fce8e5516d1b51bc7c7e62257c78ba00aed8a43a/img_Rasshirennyy_kurs_Excel_1416977721_60805_1_10.jpg)