Обобщающий урок в 6-м классе "Рациональные числа"
Цели урока
Систематизировать, расширить и углубить у учащихся знания о рациональных числах, умения выполнять действия над рациональными числами, применять знания при решении разного типа задач. Познакомить учащихся с историей возникновения и записи положительных и отрицательных чисел.
Способствовать развитию наблюдательности, умения анализировать, сравнивать, навыков самостоятельной работы.
Оборудование к уроку:
листы с печатной основой (приложение) проведения.
Карточки с заданиями
Ход урока
1. Мотивационно-ориентировочный этап
В этом году мы начали изучать новые числа. Как они называются?
Сегодня на уроке мы продолжим работу по отработке навыков действий над рациональными числами, а также познакомимся с историей развития отрицательных чисел.
Разминка.
Проводится игра «Верю – не верю» (5 минут)
Я буду вам зачитывать некоторые математические понятия, а вы должны соглашаться со мной или нет в зависимости от верности этого понятия
Верите ли вы что….?
- Рациональные числа – это положительные и отрицательные числа (целые и дробные) и ноль (да)
- Во II в. до нашей эры ни египтяне, ни вавилоняне, ни древние греки не знали отрицательных чисел. Понятие отрицательного числа появилось при решении уравнений. Еще в III веке нашей эры древнегреческий математик Диофант в своих уравнениях фактически уже пользовался правилом умножения положительных и отрицательных чисел. Но -3 для Диофанта не самостоятельное число, а всего лишь “вычитаемое”, любое положительное – прибавляемое. Отдельно взятые отрицательные числа Диофант не признавал, и если при решении уравнений получался отрицательный корень, то он отбрасывал его как “недопустимый”. (да)
- Если модуль числа больше самого числа, то оно отрицательное (да)
- Если модуль равен этому числу, то оно равно 0 (нет)
- расположение рациональных чисел на координатной прямой, о том, что «Положительные числа изображаются на числовой оси точками, лежащими вправо от начала 0, отрицательными – влево”, впервые истолковал французский математик, физик и философ Рене Декарта в своей книге «Геометрия”.
- На координатной прямой между числами -4,5 и -2 лежат 2 целых числа (да)
- Из двух чисел с разными знаками больше то, у которого модуль больше (нет)
-Сумма, разность и произведение рациональных чисел тоже рациональные числа.
- При делении рациональных чисел получается рациональное число (нет, деление на 0)
2.Операционно-исполнительский этап
Проводится проверка глубины изученного материла
Приём: Тонкие и толстые вопросы (10 минут)
| Тонкие | Толстые |
| Кто...? Что…? Когда…?
Может…? Мог ли…?
Было ли…? Будет…?
Согласны ли вы…?
Верно ли…?
| Объясните почему…?
Почему вы думаете…?
Предположите, что будет если…?
В чём различие…?
Почему вы считаете…? |
Учащиеся разбиваются на 2 группы и в течении 10 минут составляют вопросы по теме рациональные числа. Вопросы зачитываются соперникам
Самостоятельная работа практического характера:
Игра «Третий лишний»
Учащимся раздаются карточки по выбору на оценки «3», «4», «5», также карточки ложатся на свободные места. Задание: за 15 минут необходимо решить не менее 3 заданий по выбору, при условии, что предыдущее выполнил. При выборе заданий нужно пересаживаться на свободные места с заданиями. Оценка будет выставляться из среднего арифметического всех правильно выполненных заданий.
Уровень А.
Часть А состоит из 12 несложных заданий, из которых необходимо выполнить любые 8. К каждому заданию даны 4 варианта ответов, из которых только один верный. В бланке ответов поставьте под номером задания букву ответа, который на ваш взгляд является правильным.
А1. Укажите координату точки А
x
А

0
1







а) – 4; б) – 2; в) 2; г) 4.
А2. Значение выражения 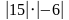 равно
равно
а) – 90; б) 9; в) 21; г) 90.
А3. Выберите число, модуль которого больше:
а) – 91,3; б) – 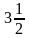 ; в)
; в) 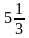 ; г) 10,8.
; г) 10,8.
А4. Найдите значение алгебраической суммы - 16 + 8.
а) – 24; б) – 8; в) 8; г) 24.
А5. Вычислите 27 – 53.
а) – 80; б) – 26; в) 16; г) 80.
А6. Найдите значение числового выражения – 25 + (- 17).
а) – 42; б) – 8; в) 8; г) 42.
А7. Решите уравнение 2,6у = 5,2.
а) – 2; б) – 0,5; в) 2; г) 2,6.
А8. Найти корень уравнения х :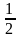 = 10.
= 10.
а) – 20; б) 5; в) 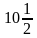 ; г) 20.
; г) 20.
А9. Найдите неизвестный член пропорции 0,2 : х = 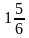 : 5.
: 5.
а) 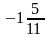 ; б) –
; б) – 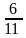 ; в)
; в) 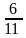 ; г)
; г) 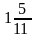 .
.
10. Найдите периметр прямоугольника со сторонами 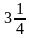 м и
м и 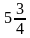 м.
м.
а) 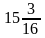 м; б) 8м; в) 9м; г) 18м.
м; б) 8м; в) 9м; г) 18м.
А11. Длина прямоугольника 30 см, ширина составляет 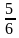 длины. Найти ширину прямоугольника.
длины. Найти ширину прямоугольника.
а) 2,5 см; б) 3,6 см; в) 25 см; г) 36 см
А12. Найти 20% от 55.
а) 1; б) 11; в) 20; г) 27,5.
Уровень В.
Часть В состоит из 3 более сложных заданий. Из заданий этой части вы можете выбрать любые 2 и записать их решения с полным обоснованием на листах бумаги.
В1. Найти значение числового выражения 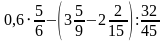 .
.
В2. В июне бригада установила 45% всех окон, а в июле – на два окна больше. Сколько окон установила бригада в июле, если всего она должна установить 320 окон?
В3. Автомобилист заметил, что со скоростью 20м/с он проехал мост через реку за 30 с. На обратном пути он проехал этот же мост за 80 с. Определить скорость автомобиля на обратном пути.
Уровень С.
Часть С состоит из 1 задания. Запишите его решение с полным обоснованием.
С1. Вычислить наиболее простым способом
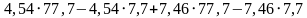 .
.
Вывод
Расставьте в порядке возрастания рациональные числа и составьте слово:
.-1 0,19 0,5 0 -0,1 3 -1,8
ы о м л ц о д
Домашняя работа подготовить ответы на тонкие и толстые вопросы соперников
Выполнить задания на обратных сторонах вопросов, выбирая разноуравневые задания.
Приложение 1
| Тонкие | Толстые |
| Кто...?
Что…?
Когда…?
Может…?
Мог ли…?
Было ли…?
Будет…?
Согласны ли вы…?
Верно ли…?
| Объясните почему…?
Почему вы думаете…?
Предположите, что будет если…?
В чём различие…?
Почему вы считаете…? |
Приложение 2
| Расположите числа в порядке возрастания: 0 -1,5 -39 -51,5 -0,1 -51,456 -1,99 -0,3 -51,1 -0,01
| Найдите пары противоположных чисел 5 5,4 3 -5 2,5 8 -0,25
|
| Сравните числа: а) – 5,2 и 8; б) -9 и -2,3; в) 0 и –78; г) – 4/7 и –5/6; д) | 45| и | –80|
| Вычислите: а) – 15,5 + 20; б) – 1,7 – 9,1; |
| Вычислите а) 56: (–8); б) – 1,44 : (– 0,2);
| Вычислите 14 9 32 16 а) --- • ---; б) ---- : -----; 27 7 35 5 |
| Вычислите 1 2 4 6 а) 2---- – 1----; б) 55--- + 34------ 8 6 5 7
| Решите уравнение: а) – 2,5 х = 10;
|
| Решите уравнение 5х – 18 = 3х +5;
| Решите уравнение –12х – 3 = 11х + 43;
|
| Найдите значение выражения: 2 1 4 – ( – 1 --- – --- ) : 52 = 3 15
| Решите уравнение: – 2 • (3 – m) = 3 ( 4 – m) + 5 |
| Найдите периметр прямоугольника со сторонами 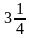 м и м и 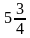 м. м.
| Длина прямоугольника 30 см, ширина составляет 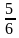 длины. Найти ширину прямоугольника. длины. Найти ширину прямоугольника.
|
| С двух полей собрали 21,7 т зерна. Сколько тонн зерна собрали с каждого поля, если с одного из них собрали на 2, 3т зерна больше, чем с другого?
| Составьте буквенное выражение: частное от деления разности чисел 9,3n и 4,8n, на 1,5. Найдите его значение, если n = 0,44.
|
| Найдите неизвестный член пропорции 0,2 : х = 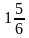 : 5. : 5.
| В июне бригада установила 45% всех окон, а в июле – на два окна больше. Сколько окон установила бригада в июле, если всего она должна установить 320 окон?
|
| Найти значение числового выражения 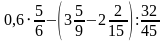
| Вычислить наиболее простым способом 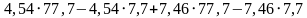 . .
|










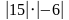 равно
равно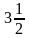 ; в)
; в) 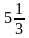 ; г) 10,8.
; г) 10,8.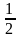 = 10.
= 10.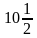 ; г) 20.
; г) 20. 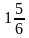 : 5.
: 5.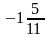 ; б) –
; б) – 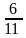 ; в)
; в) 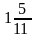 .
.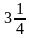 м и
м и 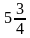 м.
м.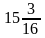 м; б) 8м; в) 9м; г) 18м.
м; б) 8м; в) 9м; г) 18м.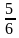 длины. Найти ширину прямоугольника.
длины. Найти ширину прямоугольника.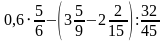 .
.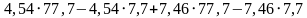 .
.









