Пояснительная записка
Рабочая программа учебного предмета «Алгебра и начала анализа» составлена на основании федерального компонента государственного стандарта основного общего образования по математике, примерной и авторской программы основного общего образования по математике «Программы. Математика. 5-6 классы Алгебра. 7-9 классы. Алгебра и начала математического анализа 10-11 классы» ( авт.- сост. И.И. Зубарева, А.Г, Мордкович. – 2-е изд., испр. и доп.. – М.: Мнемозина, 2009. – 63 с.).
Программа соответствует учебнику для учащихся общеобразовательных учреждений (профильный уровень) «Алгебра и начала математического анализа. 11 класс. В 2-х частях» А. Г. Мордкович, П.В.Семенов – М. Мнемозина, 2012-2013 гг./ и обеспечена учебно-методическим комплектом «Алгебра и начала математического анализа» А.Г, Мордкович. (М.: Мнемозина 2013 г.).
Согласно действующему в школе учебному плану календарно-тематический план предусматривает следующий вариант организации процесса обучения:
в 11 классе профильного уровня предполагается обучение в объеме 136 часов в год (4 часа в неделю).
Общая характеристика учебного предмета.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры. Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах. При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления. Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умениия логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Цели преподавания предмета:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Общеучебные умения, навыки и способы деятельности.
В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования; поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Требования к уровню подготовки выпускников:
Знать:
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрического языка как средства описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знаний и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира;
Уметь:
выполнять арифметические действия;
проводить преобразования числовых и буквенных выражений;
определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций, выполнять преобразование графиков; описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства;
вычислять производные элементарных функций; исследовать и строить графики элементарных функций с помощью производной;
решать уравнения; доказывать несложные неравенства;
решать текстовые задачи с помощью уравнений и неравенств;
решать простейшие комбинаторные задачи; вычислять вероятность событий на основе подсчета числа исходов (простейшие случаи);
соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;
изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними;
проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
применять координатно-векторный метод для вычисления отношений, расстояний и углов;
строить сечения многогранников и изображать сечения тел вращения.
Использование приобретенных знаний и умений в практической деятельности и повседневной жизни:
для практических расчетов по формулам, включая формулы, содержащие степени, радикалы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
для описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов;
решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшее и наименьшее значения с применением аппарата математического анализа;
построения и исследования простейших математических моделей;
анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера;
для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
для вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Содержание программы
Многочлены. (10 ч)
Многочлены от одной и нескольких переменных. Теорема Безу. Схема Горнера. Симметрические и однородные многочлены. Уравнения высших степеней.
Степени и корни. Степенные функции (24 ч)
Понятие корня n-ой степени из действительного числа. Функции y=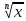 их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Дифференцирование и интегрирование. Извлечение корней n-ой степени из комплексных чисел.
их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Дифференцирование и интегрирование. Извлечение корней n-ой степени из комплексных чисел.
Показательная и логарифмическая функции (31 ч)
Показательная функция, её свойства и график. Показательные уравнения и неравенства. Понятие логарифма. Логарифмическая функция, её свойства и график. Свойства логарифмов. Логарифмические уравнения и неравенства. Дифференцирование показательной и логарифмической функций.
Первообразная и интеграл (9 ч)
Первообразная и неопределенный интеграл. Определенный интеграл, его вычисление и свойства. Вычисление площадей плоских фигур. Примеры применения интеграла в физике.
Элементы комбинаторики, статистики и теории вероятностей (9 ч).
Вероятность и геометрия. Независимые повторения испытаний с двумя исходами. Статистические методы обработки результатов. Гауссова кривая. Закон больших чисел.
Уравнения и неравенства. Системы уравнений и неравенств (33 ч).
Равносильность уравнений. Общие методы решения систем уравнений. Уравнения с модулями. Иррациональные уравнения. Доказательство неравенств. Решение рациональных неравенств с одной переменной. Неравенства с модулями. Иррациональные неравенства. Уравнения и неравенства с двумя переменными. Диофантовы уравнения. Системы уравнений. Уравнения и неравенства с параметрами.
Cистема оценки знаний учащихся.
Оценка устных ответов учащихся.
Оценка 5 ставится в том случае, если учащийся демонстрирует полное понимание сути теории и свободно оперирует ей, творчески применяет теоретические знания на практике. При решении задач наблюдаются четко осознанные действия. Решает нестандартные задачи. Не допускает вычислительных ошибок. Умеет самостоятельно получать знания, работая с дополнительной литературой (учебником, компьютером, справочной литературой)
Оценка 4 ставится в том случае, если ответ ученика удовлетворяет основным требованиям к ответу на оценку 5, но без использования собственного плана, новых примеров, без применения знаний в новой ситуации, без использования связей с ранее изученным материалом, усвоенным при изучении других предметов. Не задумываясь решает задачи по известному алгоритму, проявляет способность к самостоятельным выводам. Допускает вычислительные ошибки крайне редко и, если учащийся допустил одну ошибку или не более двух недочетов, то может исправить их самостоятельно или с небольшой помощью учителя.
Оценка 3 ставится в том случае, если учащийся запомнил большую часть теоретического материала, без которого невозможна практическая работа по теме. Решает самостоятельно только те практические задачи, в которых известен алгоритм, а остальные задания может выполнить только с помощью учителя и учащихся. Допускает много вычислительных ошибок.
Оценка 2 ставится в том случае, если учащийся не овладел основными знаниями в соответствии с требованиями и допустил больше ошибок и недочетов, чем необходимо для оценки 3. Не может выполнить ни одного практического задания с применением данной теории.
Оценка письменных контрольных работ.
Оценка 5 ставится за работу, выполненную полностью без ошибок и недочетов.
Оценка 4 ставится за работу, выполненную полностью, но при наличии не более одной ошибки и одного недочета, не более трех недочетов.
Оценка 3 ставится за работу, выполненную на 1/2 всей работы правильно или при допущении не более одной грубой ошибки, не более трех негрубых ошибок, одной негрубой ошибки и трех недочетов, при наличии четырех-пяти недочетов.
Оценка 2 ставится за работу, в которой число ошибок и недочетов превысило норму для оценки 3 или правильно выполнено менее 1/2 работы.
Тематическое планирование
Алгебра и начала анализа
11 класс.
Профильный уровень
4 часа в неделю, 136 часов в год
| № | Тема | Кол. часов | ЗУН |
| 1-3 | Повторение материала 10 класса | 3 | Знать: основные формулы, алгоритмы решения тригонометрических уравнений и неравенст; схему исследования функций. Уметь: применять на практике формулы и алгоритмы. |
| 4 | Входная контрольная работа | 1 |
|
| Глава 1. Многочлены. (10 ч) |
| 5-7 | Многочлены от одной переменной | 3 | Знать: понятие многочлена от одной переменной Уметь: проводить арифметические операции, деление многочлена на многочлен с остатком, раскладывать многочлен на множители |
| 8-10 | Многочлены от нескольких переменных | 3 | Знать: определение многочлена от нескольких переменных Уметь: решать уравнение с несколькими неизвестными, решать симметрические системы уравнений |
| 11-13 | Уравнения высших степеней | 3 | Знать: определение уравнения высшей степени Уметь: преобразовывать уравнение в приведенное уравнение с целыми коэффициентами |
| 14 | Контрольная работа №1. | 1 |
|
| Глава 2. Степени и корни. Степенные функции (24 ч) |
| 15-16 | Понятие корня n-ой степени из действительного числа | 2 | Знать: понятие квадратного корня, понятие корня n-ой степени и его свойства Уметь: находить корни n-ой степени из чисел |
| 17-19 | Функции у=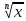 , их свойства и графики , их свойства и графики | 3 | Знать: свойства функции у=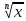 Уметь: строить графики |
| 20-22 | Свойства корня n-ой степени | 3 | Знать: понятие корня n-ой степени и его свойства Уметь: применять свойства на практике |
| 23-26 | Преобразование выражений, содержащих радикалы | 4 | Знать: свойства функции у= понятие корня n-ой степени и его свойства понятие корня n-ой степени и его свойства Уметь: применять на практике понятие о показатели степени, научиться осуществлять преобразование выражений, содержащих операцию извлечения корня. |
| 27-28 | Контрольная работа № 2. | 2 |
|
| 29-31 | Понятие степени с любым рациональным показателем | 3 | Знать: определение степени с рациональным показателем, область допустимых значений переменных в выражениях, содержащих степень с любым рациональным показателем Уметь: применять свойства на практике |
| 32-35 | Степенные функции, их свойства и графики | 4 | Знать: понятие степенной функции, свойства степенных функций, ее графики и свойства Уметь: строить графики, применять свойства функций |
| 36-37 | Извлечение корней из комплексных чисел | 2 | Знать: определение корня n-ой степени из комплексного числа Уметь: применять основную теорему алгебры |
| 38 | Контрольная работа № 3. | 1 |
|
| Глава 3. Показательная и логарифмическая функции (31 ч) |
| 39-41 | Показательная функция, её свойства и график | 3 | Знать: понятие показательной функции, ее свойства Уметь: строить графики |
| 42-44 | Показательные уравнения | 3 | Знать: алгоритмы решения показательных уравнений Уметь: решать показательные уравнения |
| 45-46 | Показательные неравенства | 2 | Знать: алгоритмы решения показательных неравенств Уметь: решать показательные неравенства |
| 47-48 | Понятие логарифма | 2 | Знать: определение логарифма Уметь: вычислять логарифмы |
| 49-51 | Логарифмическая функция, её свойства и график | 3 | Знать: понятие логарифма, свойства логарифмической функции Уметь: строить графики |
| 52-53 | Контрольная работа № 4. | 2 |
|
| 54-57 | Свойства логарифмов | 4 | Знать: свойства логарифмов Уметь: применять на практике |
| 58-61 | Логарифмические уравнения | 4 | Знать: понятие логарифмического уравнения, методы решения логарифмических уравнений Уметь: решать логарифмические уравнения |
| 62-64 | Логарифмические неравенства | 3 | Знать: понятие логарифмического неравенства, методы решения логарифмических неравенств Уметь: решать логарифмические неравенства |
| 65-67 | Дифференцирование показательной и логарифмической функций | 3 | Знать: формулы и правила дифференцирования Уметь: применять для дифференцирования показательной и логарифмических функций |
| 68-69 | Контрольная работа № 5. | 2 |
|
| Глава 4. Первообразная и интеграл (9 ч) |
| 70-72 | Первообразная и неопределенный интеграл | 3 | Знать: понятие первообразной, неопределенного интеграла, формулы для нахождения первообразных Уметь: вычислять первообразную, находить неопределенный интеграл |
| 73-77 | Определенный интеграл | 5 | Знать: понятие определенного интеграла, формулы для вычисления определенного интеграла Уметь: решать задачи, приводящие к понятию определенного интеграла |
| 78 | Контрольная работа № 6 | 1 |
|
| Глава 5. Элементы комбинаторики, статистики и теории вероятностей (9 ч). |
| 79-80 | Вероятность и геометрия | 2 | Знать: классическое определение вероятности Уметь: строить классическую вероятностную схему, применять правило нахождения геометрических вероятностей |
| 81-83 | Независимые повторения испытаний с двумя исходами | 3 | Знать: схему Бернулли Уметь: применять правило нахождения наивероятнейшего числа успехов в n испытаниях Бернулли |
| 84-85 | Статистические методы обработки информации | 2 | Знать: понятие элементов теории вероятности и математической статистики Уметь: применять простейшие методы статистической обработки информации |
| 86-87 | Гауссова кривая. Закон больших чисел | 2 | Знать: алгоритмы использования функции y=ф(х) в приближенных вычислениях Уметь: применять изученные формулы для упрощения выражений |
| Глава 6. Уравнения и неравенства. Системы уравнений и неравенств (33 ч). |
| 88-91 | Равносильность уравнений | 4 | Знать: определение уравнений, корней уравнений, равносильных уравнений. Уметь: применять теорему о равносильности уравнений |
| 92-94 | Общие методы решения уравнений | 3 | Знать: знать метод замены уравнения, метод разложения на множители, метод введений новой переменной Уметь: применять общие методы решения уравнений |
| 95-97 | Равносильность неравенств | 3 | Знать: определение равносильных неравенств Уметь: применять теоремы о равносильности неравенств |
| 98-100 | Уравнения и неравенства с модулями | 3 | Знать: способы решения уравнений и неравенств с модулями Уметь: решать уравнения и неравенства с модулями |
| 101-102 | Контрольная работа № 7 | 2 |
|
| 103-105 | Уравнения и неравенства со знаком радикала | 3 | Знать: определение иррациональных уравнений и неравенств, способы решения иррациональных уравнений и неравенств Уметь: решать иррациональные уравнения и неравенства различными методами |
| 106-107 | Уравнения и неравенства с двумя переменными | 2 | Знать: способы решения уравнений и неравенств с двумя переменными Уметь: решать уравнения и неравенства с двумя переменными |
| 108-110 | Доказательство неравенств | 3 | Знать: доказательство неравенств с помощью определения Уметь: применять синтетический метод доказательства неравенств |
| 111-114 | Системы уравнений | 4 | Знать: определение решения системы уравнений и равносильности систем Уметь: решать системы уравнений различными способами |
| 115-116 | Контрольная работа № 8 | 2 |
|
| 117-120 | Задачи с параметрами | 4 | Знать: определения уравнения с параметрами Уметь: решать уравнение с параметрами аналитически и графически |
| 121-136 | Обобщающее повторение | 16 |
|
Контрольная работа №1 (1 час)
Вариант 1
Дан многочлен 
а) Приведите данный многочлен к стандартному виду.
б) Установите, является ли данный многочлен однородным.
в) Если многочлен является однородным, то определите его степень.
Разложите многочлен на множители:
а)  б)
б) 
Решите уравнение: 
Докажите, что выражение  делится на
делится на 
При каких значениях параметров  и
и  многочлен
многочлен  делится без остатка на многочлен
делится без остатка на многочлен 
Вариант 2
Дан многочлен 
а) Приведите данный многочлен к стандартному виду.
б) Установите, является ли данный многочлен однородным.
в) Если многочлен является однородным, то определите его степень.
Разложите многочлен на множители:
а)  б)
б) 
Решите уравнение: 
Докажите, что выражение  делится на
делится на 
При каких значениях параметров  и
и  многочлен
многочлен  делится без остатка на многочлен
делится без остатка на многочлен 
Контрольная работа №2 (2 часа)
Вариант 1
Вычислите: а)  б)
б) 
Решите уравнение: а)  б)
б) 
Постройте график функции: 
Найдите область определения функции
Упростите выражение 
Расположите в порядке убывания следующие числа: 
Упростите выражение  , найдите его значение при
, найдите его значение при 
Решите неравенство 
Решите уравнение: 
Вариант 2
Вычислите: а)  б)
б) 
Решите уравнение: а)  б)
б) 
Постройте график функции: 
Найдите область определения функции
Упростите выражение 
Расположите в порядке убывания следующие числа: 
Упростите выражение ,найдите его значение при
,найдите его значение при 
Решите неравенство 
Решите уравнение: 
Контрольная работа №3 (1 час)
Вариант 1
Вычислите: а)  б)
б) 
Упростите выражение:
Решите уравнение: 
Составьте уравнение касательной к графику функции  в точке х=1.
в точке х=1.
Решите неравенство
Решите уравнение на множестве комплексных чисел.
на множестве комплексных чисел.
Контрольная работа №3 (1 час)
Вариант 2
Вычислите: а)  б)
б) 
Упростите выражение: 
Решите уравнение: 
Составьте уравнение касательной к графику функции  в точке х=1.
в точке х=1.
Решите неравенство 
Решите уравнение  на множестве комплексных чисел.
на множестве комплексных чисел.
Контрольная работа №4 (2 часа)
Вариант 1
Постройте график функции: а)  б)
б) 
Решите уравнение: а)  б)
б) 
Решите неравенство: 
Вычислите: 
Сравните числа a и b, если: а)  б)
б) 
Решите неравенство: 
Решите неравенство: 
Контрольная работа №4 (2 часа)
Вариант 2
Постройте график функции: а)  б)
б) 
Решите уравнение: а)  б)
б) 
Решите неравенство: 
Вычислите: 
Сравните числа a и b, если: а)  б)
б) 
Решите неравенство: 
Решите неравенство: 
Контрольная работа № 5 (2 часа)
Вариант 1
Вычислите 
Решите уравнение: а) 
б) 
в) 
Решите неравенство: а)  б)
б) 
Исследуйте функцию  на монотонность и экстремумы.
на монотонность и экстремумы.
К графику функции  проведена касательная, параллельная прямой
проведена касательная, параллельная прямой  . Найдите точку пересечения этой касательной с осью х.
. Найдите точку пересечения этой касательной с осью х.
Решите неравенство: 
Решите систему уравнений 
Контрольная работа № 5 (2 часа)
Вариант 2
Вычислите 
Решите уравнение: а) 
б) 
в) 
Решите неравенство: а)  б)
б) 
Исследуйте функцию  на монотонность и экстремумы.
на монотонность и экстремумы.
К графику функции  проведена касательная, параллельная биссектрисе первой координатной четверти. Найдите площадь треугольника, образованного этой касательной и осями координат.
проведена касательная, параллельная биссектрисе первой координатной четверти. Найдите площадь треугольника, образованного этой касательной и осями координат.
Решите неравенство: 
Решите систему уравнений 
Контрольная работа №6 (1 час)
Вариант 1
Докажите, что функция  является первообразной для функции
является первообразной для функции  .
.
Для функции  найдите ту первообразную, график которой проходит через заданную А (-3;-2).
найдите ту первообразную, график которой проходит через заданную А (-3;-2).
Вычислите определённый интеграл: а)  ; б)
; б)  .
.
Найдите площадь фигуры, ограниченной линиями  .
.
Известно, что функция  – первообразная для функции
– первообразная для функции  . Исследуйте функцию
. Исследуйте функцию  на монотонность и экстремумы.
на монотонность и экстремумы.
При каких значениях параметра а выполняется неравенство  ?
?
Контрольная работа №6 (1 час)
Вариант 2
Докажите, что функция  является первообразной для функции
является первообразной для функции  .
.
Для функции  найдите ту первообразную, график которой проходит через заданную А (1;-5).
найдите ту первообразную, график которой проходит через заданную А (1;-5).
Вычислите определённый интеграл: а)  ; б)
; б)  .
.
Найдите площадь фигуры, ограниченной линиями  .
.
Известно, что функция  – первообразная для функции
– первообразная для функции  . Исследуйте функцию
. Исследуйте функцию  на монотонность и экстремумы.
на монотонность и экстремумы.
При каких значениях параметра b выполняется неравенство  ?
?
Контрольная работа №7 (2 часа)
Вариант 1
Решите уравнение: а) 
б) 
в) 
Решите неравенство: а)  б)
б) 
Решите уравнение 
Решите уравнение 
Внутри равнобедренного прямоугольного треугольника случайным образом выбрана точка. Какова вероятность того, что она расположена ближе к вершине прямого угла, чем к вершинам острых углов треугольника?
Решите уравнение: 
Контрольная работа №7 (2 часа)
Вариант 2
Решите уравнение: а) 
б) 
в) 
Решите неравенство: а)  б)
б) 
Решите уравнение 
Решите уравнение 
Внутри квадрата случайным образом выбрана точка. Какова вероятность того, что она расположена внутри вписанного в него круга?
Решите уравнение: 
Контрольная работа №8 (2 часа)
Вариант 1
Решите уравнение: а)  б)
б) 
Решите неравенство: а) 
Решите систему уравнений: а) б)
б) 
Найдите площадь фигуры, заданной системой неравенств 
Докажите, что для любых неотрицательных чисел a и b выполняется неравенство 
Решите уравнение в целых числах 
Три данных числа образуют арифметическую прогрессию. Если третий член прогрессии уменьшить на 3, то полученные три числа составят геометрическую прогрессию. Если второй член этой геометрической прогрессии уменьшить на  , то полученные три числа вновь составят геометрическую прогрессию. Найдите данные числа.
, то полученные три числа вновь составят геометрическую прогрессию. Найдите данные числа.
Контрольная работа №8 (2 часа)
Вариант 2
Решите уравнение: а)  б)
б) 
Решите неравенство: а) 
Решите систему уравнений: а) б)
б) 
Найдите площадь фигуры, заданной системой неравенств 
Докажите, что для любых неотрицательных чисел a, b и с выполняется неравенство 
Решите уравнение в целых числах 
Три данных числа образуют геометрическую прогрессию. Если второй член прогрессии увеличить на 2, то полученные числа составят арифметическую прогрессию. Если третий член новой прогрессии увеличить на 9, то полученные три числа составят геометрическую прогрессию. Найдите данные числа.







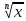 их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Дифференцирование и интегрирование. Извлечение корней n-ой степени из комплексных чисел.
их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Дифференцирование и интегрирование. Извлечение корней n-ой степени из комплексных чисел. понятие корня n-ой степени и его свойства
понятие корня n-ой степени и его свойства



















