Презентация "Равнобедренный треугольник и его свойства"

«Равнобедренный треугольник и его свойства»

Боковая сторона

Определение: Треугольник называется равнобедренным, если две его стороны равны.

B

A

C

Основание

Определение: Треугольник называется равносторонним, если все его стороны равны.

E

F

D

A

B

C

A

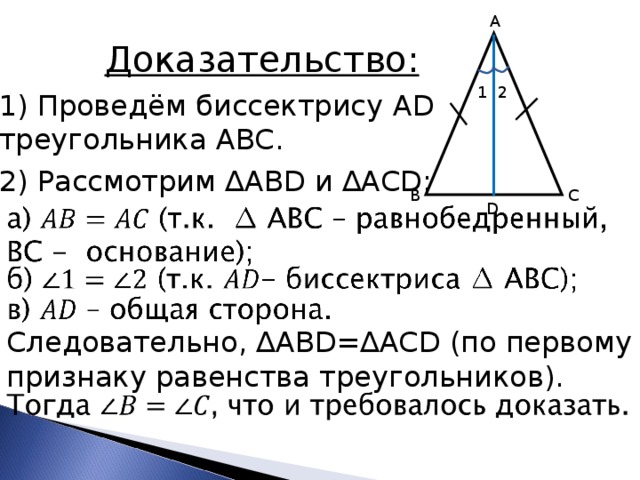
Доказательство:

1

2

1) Проведём биссектрису AD треугольника АВС.

2) Рассмотрим ∆ ABD и ∆ ACD :

C

B

D

Следовательно, ∆ ABD =∆ ACD (по первому признаку равенства треугольников).

Теорема 2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Дано: ∆ ABC – равнобедренный,

ВС - основание,

AD -биссектриса.

Доказать: AD -медиана,

AD -высота.

Доказательство:

1) Рассмотрим ∆ ABD и ∆ ACD :

Следовательно, ∆ ABD =∆ ACD (по первому признаку равенства треугольников).

1. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.

2. Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.

A

B

C

В равнобедренном треугольнике ABC проведена биссектриса AD к основанию. Отрезок BD равен 7 см. Найдите основание треугольника.

A

B

C

D