© 2022, Хубазова Анжелла Мовлдиевна 178 1


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока





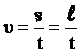 .
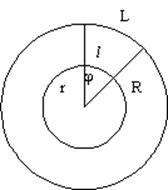
.
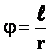 .
.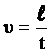
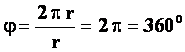 - полный оборот точки соответствует 2π радиан. Для перевода единиц составим пропорцию:
- полный оборот точки соответствует 2π радиан. Для перевода единиц составим пропорцию: 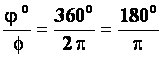 . Следовательно:
. Следовательно: 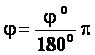
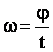 - угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ - рад/с.
- угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ - рад/с.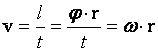 , т.е.
, т.е.  .
.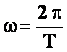 .
.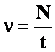 .
.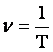 . Следовательно:
. Следовательно: 









