Равновеликие и равносоставленные фигуры

Урок 18: «Равновеликие и равносоставленные фигуры»

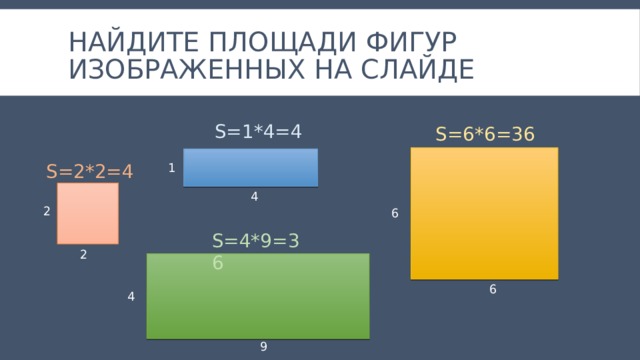
Найдите площади фигур изображенных на слайде

S=1*4=4

S=6*6=36

S=2*2=4

1

4

2

6

S=4*9=36

2

6

4

9

Равновеликие фигуры

• Вычислив площади двух, на первый взгляд разных фигуры, мы выяснили, что квадрат и прямоугольник, изображенные на слайде имеют одинаковую площадь.

ОПРЕДЕЛЕНИЕ: Две фигуры, имеющие одинаковую площадь, называются равновеликими

S=2*2=4

S=1*4=4

2

1

4

2

Равновеликие и равносоставленные фигуры

• На рисунке красный прямоугольник и желтый квадрат являются равновеликими.
• Закрашенные на них многоугольники также являются равновеликими.

Если из равных величин вычесть поровну, то поровну и останется.

Если фигура разрезана на части, то её площадь равна сумме площадей её частей.

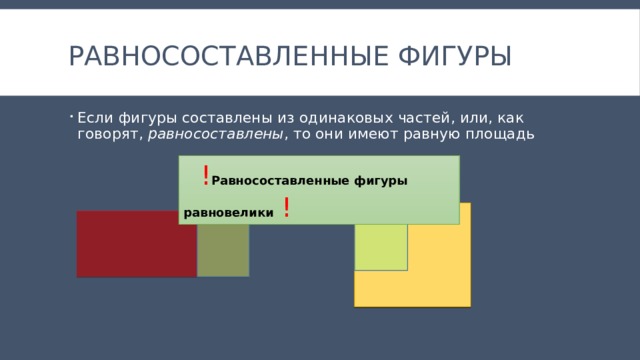
равносоставленные фигуры

• Если фигуры составлены из одинаковых частей, или, как говорят, равносоставлены , то они имеют равную площадь

! Равносоставленные фигуры равновелики !

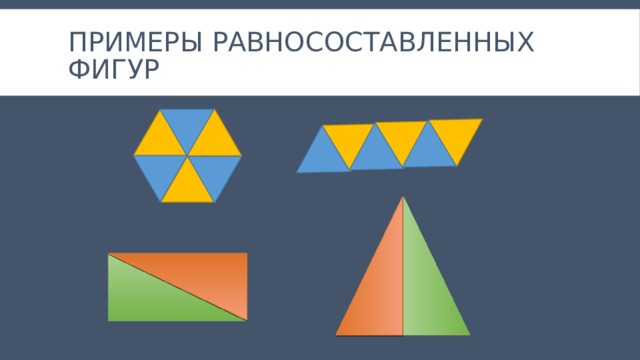
Примеры равносоставленных фигур

На странице 214(до абзаца «площади параллелограмма и треугольника») учебника МАТЕМАТИКА. Арифметика. Геометрия. Автора Е.А. Бунимович, вы ещё раз можете ознакомиться с темой «равновеликие и равносоставленные фигуры».

Задание 1: Нарисуйте какой-нибудь прямоугольник, равновеликий квадрату со стороной 6 см. Сколько существует прямоугольников с такой площадью, длины сторон которых (в см) выражаются целыми числами?

Вспомним! Две фигуры, имеющие одинаковую площадь, называются равновеликими .

Следовательно, площадь квадрата с стороной 6 см равна 36,

S=6*6=36 (см 2 ).

Мы можем построить прямоугольники той же площади ( 36 см 2 ). Например со сторонами 2 и 18.

Существуют прямоугольники площадью 36 (см 2 ) со сторонами: a=1, b=36; a=2, b=18; a=3, b=12; a=4, b=9; a=6, b=6;

2

18

Ответ: Всего мы можем нарисовать 6 прямоугольников площадью 36 (см 2 )

Задание 2. Два одинаковых квадрата расположены так, как показано на рисунке. Докажите, что сумма площадей темных треугольников равна сумме площадей белых треугольников

• По условию площади квадратов равны.
• Площадь зеленого квадрата равна площади шестиугольника и 4 зеленым треугольникам.
• Из того, что площади квадратов равны следует, что сумма площадей шестиугольника и 4 зеленых треугольников равна сумме площадей шестиугольника и 4 белых треугольников.
• Так как площадь шестиугольника является общей для обоих квадратов, следует, что сумма площадей темных треугольников равна сумме площадей белых треугольников.

Выберите настроение и эмоциональное состояние после урока

Домашнее задание

• К следующему уроку: параграф 46 (до абзаца «Площади параллелограмма и треугольника») №712, №713, №715 устно

Спасибо за внимание!