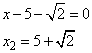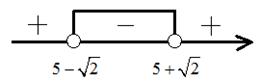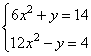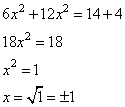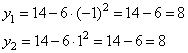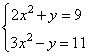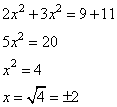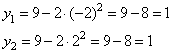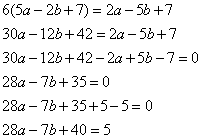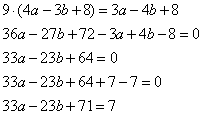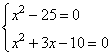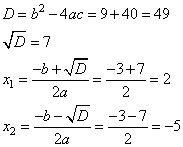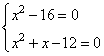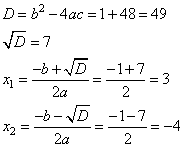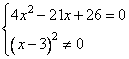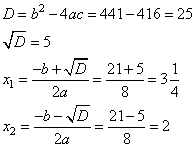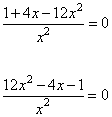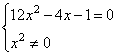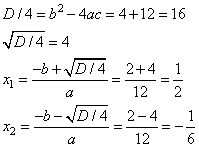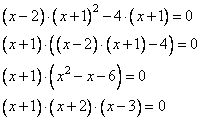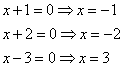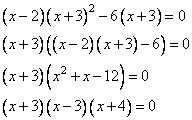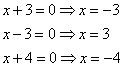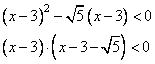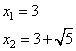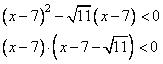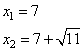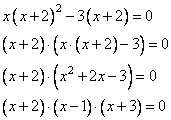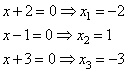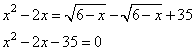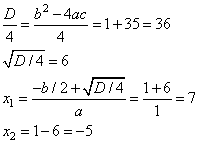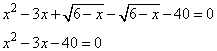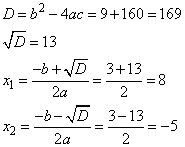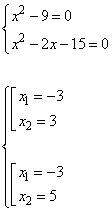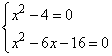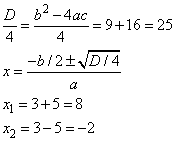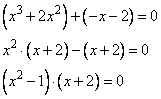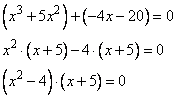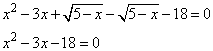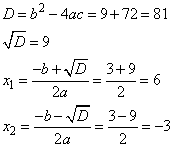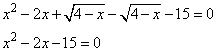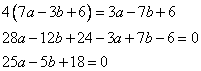Задание 21. Решите систему уравнений 
Решение.
Для решения данной системы можно вычесть второе уравнение из первого, это позволит избавиться от переменной y, получим:
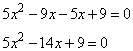
Решаем квадратное уравнение через дискриминант, имеем два корня:
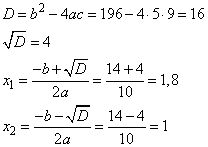
Для каждого из найденных корней найдем соответствующее значение y, подставив 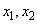 во второе уравнение:
во второе уравнение:
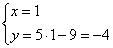 и
и 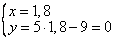
Ответ: (1;-4), (1,8; 0).
Задание 21. Решите систему уравнений 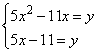
Решение.
Так как оба уравнения равны одному и тому же значению y, то их можно приравнять, получим:
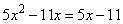 ,
,
откуда
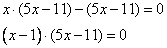
Полученное выражение будет равно 0, если
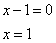 или
или 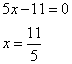
Найдем теперь значения y для каждого x, имеем:
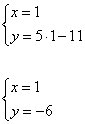 и
и 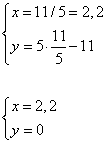
Ответ: (1;-6), (2,2; 0).
Задание 21. Решите систему уравнений 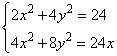
Решение.
Разделим первое уравнение на 2, а второе – на 4, получим:
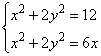
Видим, что у обоих уравнений есть слагаемое 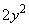 . Чтобы избавиться от него, вычтем из первого уравнения второе:
. Чтобы избавиться от него, вычтем из первого уравнения второе:
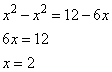
Теперь вычислим значение y при x=2, подставив x в первое уравнение, имеем:
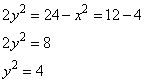
следовательно,
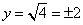 .
.
Таким образом, имеем решение (2, -2), (2,2).
Ответ: (2, -2), (2,2).
Задание 21. Решите систему уравнений 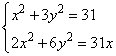
Решение.
Разделим второе уравнение на 2, получим систему
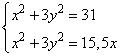
и вычтем из первого уравнения второе:
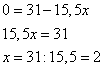
Для значения x=2 найдем соответствующие значения y, подставив x в первое уравнение:
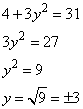
То есть имеем два решения: (2;-3) и (2;3).
Ответ: (2;-3), (2;3).
Задание 21. Решите уравнение 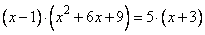
Решение.
Преобразуем уравнение, приведем его к следующему виду:
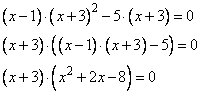
Полученное выражение будет равно 0, если
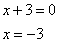
или, если
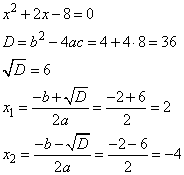
Таким образом, получили следующие корни: -4; -3; 2.
Ответ: -4; -3; 2.
Задание 21. Решите уравнение 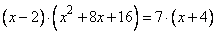 .
.
Решение.
Упростим выражение, перепишем его в следующем виде:
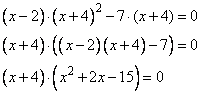
Полученное выражение будет равно 0, если
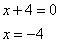
или когда
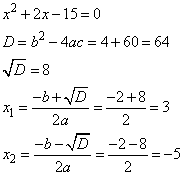
Получили три корня: -5; -4; 3.
Ответ: -5; -4; 3.
Задание 21. Решите систему уравнений 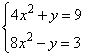
Решение.
Сложим оба уравнения, получим:
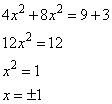
Для найденных корней x вычислим из первой формулы соответствующие значения y, имеем:
- для 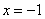 :
: 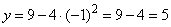 ;
;
- для 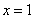 :
: 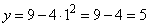 .
.
Получили два решения: (-1;5), (1;5).
Ответ: (-1;5), (1;5).
Задание 21. Решите систему уравнений 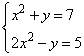
Решение.
Сложим оба уравнения, получим:
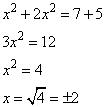
Вычислим соответствующие значения y при x=-2 и 2, подставив эти значения в первую формулу системы:
- при x=-2: 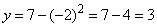 ;
;
- при x=2: 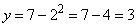 .
.
Имеем следующие решения: (-2; 3) и (2; 3).
Ответ: (-2; 3) и (2; 3).
Задание 21. Решите неравенство 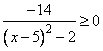 .
.
Решение.
Можно заметить, что данное неравенство будет больше либо равно 0, если
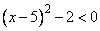 .
.
Преобразуем данное выражение, перепишем его в виде:

Из последнего выражения имеем две точки, делящие числовую ось:
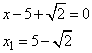 и
и 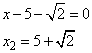
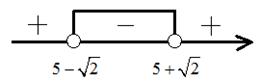
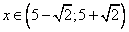 .
.
Ответ: 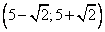 .
.
Задание 21. Решите неравенство 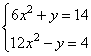
Решение.
Сложим оба уравнения системы, избавимся таким образом от переменной y, получим:
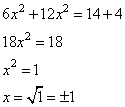
Теперь, для каждого из найденных x, вычислим y из первого уравнения:
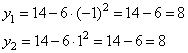
Получаем решения: (-1; 8), (1; 8).
Ответ: (-1; 8), (1; 8).
Задание 21. Решите неравенство 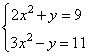
Решение.
Сложим оба уравнения системы, избавимся от переменной y, получим:
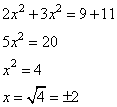
Для каждого найденного корня x вычислим соответствующее значение y из первого уравнения, имеем:
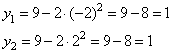
То есть получили следующие решения: (-2; 1), (2; 1).
Ответ: (-2; 1), (2; 1).
Задание 21. Найдите значение выражения 28a-7b+40, если 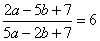 .
.
Решение.
Приведем выражение 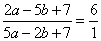 к виду
к виду 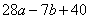 , получим:
, получим:
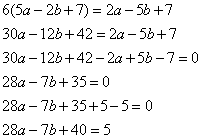
Ответ: 5.
Задание 21. Найдите значение выражения 33a-23b+71, если 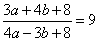 .
.
Решение.
Приведем выражение 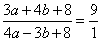 к выражению
к выражению 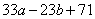 , получим:
, получим:
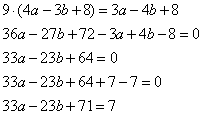
Ответ: 7.
Задание 21. Решите уравнение 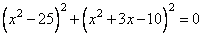 .
.
Решение.
Учитывая, что слагаемые в уравнении всегда больше либо равны 0, то уравнение будет равно нулю, если каждое из слагаемых равно нулю. Соответственно, получаем следующую систему уравнений:
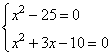
Из первого уравнения имеем корни
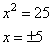
Из второго уравнения, получаем следующие два корня:
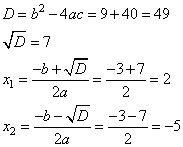
Из полученных значений видно, что оба уравнения одновременно будут принимать значение 0 при x=-5.
Ответ: -5.
Задание 21. Решите уравнение  .
.
Решение.
Любое число в квадрате всегда больше 0, следовательно, уравнение будет равно 0, если оба слагаемых равны 0. Это условие можно записать в виде следующей системы:
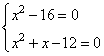
Из первого уравнения получаем два корня:
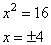
Из второго уравнения, имеем корни:
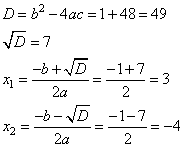
Общий корень, при котором оба уравнения переходят в 0, равен -4.
Ответ: -4.
Задание 21. Решите уравнение 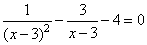 .
.
Решение.
Упростим уравнение, приведем его к следующему виду:

Данное уравнение будет равно 0, если
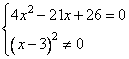
Решаем первое квадратное уравнение, получаем корни:
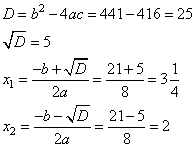
Оба корня удовлетворяют неравенству 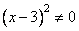 , следовательно, они являются решениями уравнения.
, следовательно, они являются решениями уравнения.
Ответ: 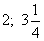 .
.
Задание 21. Решите уравнение 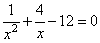 .
.
Решение.
Преобразуем уравнение к виду
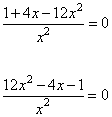
Данное уравнение будет равно 0, если
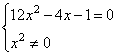
Найдем корни уравнения из квадратного уравнения:
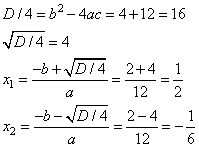
Оба корня не равны 0, следовательно, являются решениями уравнения.
Ответ: 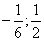 .
.
Задание 21. Решите уравнение 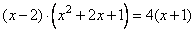 .
.
Решение.
Сначала преобразуем выражение, получим:
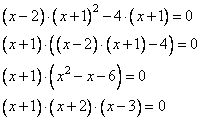
Последнее выражение показывает, что уравнение будет равно 0, если хотя бы один из множителей будет равен 0, то есть имеем 3 уравнения и 3 корня:
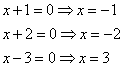
Ответ: -2; -1; 3.
Задание 21. Решите уравнение 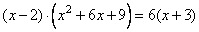 .
.
Решение.
Сначала выполним преобразование уравнения, получим:
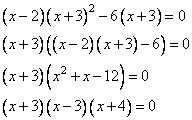
Последнее выражение показывает, что уравнение будет равно, если хотя бы один из множителей равен 0, то есть имеем следующие три уравнения:
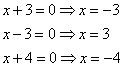
Ответ: -4; -3; 3.
Задание 21. Решите неравенство 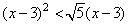 .
.
Решение.
Преобразуем неравенство, приведем его к виду:
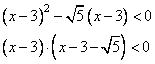
Полученное выражение дает две точки, делящие числовую ось:
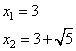

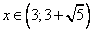 .
.
Ответ: 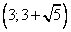 .
.
Задание 21. Решите неравенство 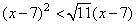 .
.
Решение.
Перепишем неравенство в следующем виде:
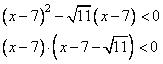
Из последнего выражения имеем две точки, делящие числовую ось:
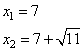
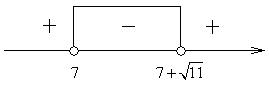
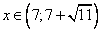 .
.
Ответ: 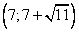 .
.
Задание 21. Решите уравнение 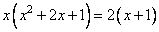 .
.
Решение.
Выполним следующее преобразование уравнения:

Полученное выражение будет равно 0, если хотя бы один из множителей равен 0, то есть имеем три уравнения и три корня:

Ответ: -2; -1; 1.
Задание 21. Решите уравнение  .
.
Решение.
Перепишем уравнение в следующем виде:
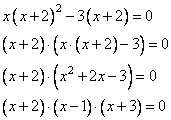
Последнее выражение принимает нулевое значение, когда хотя бы один из множителей равен 0, то есть имеем три следующих корня:
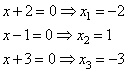
Ответ: -3; -2; 1.
Задание 21. Решите уравнение 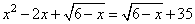 .
.
Решение.
Решим уравнение при условии, что 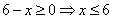 , получим:
, получим:
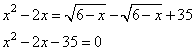
Решим квадратное уравнение с помощью дискриминанта, имеем:
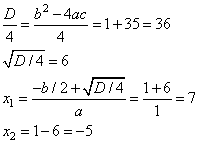
Значение 7 не входит в диапазон 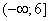 , остается только один корень -5.
, остается только один корень -5.
Ответ: -5.
Задание 21. Решите уравнение 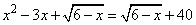 .
.
Решение.
1. Запишем ОДЗ уравнения:
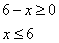
2. Упростим уравнение, приведем его к виду:
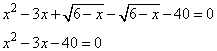
Решаем квадратное уравнение, имеем два корня:
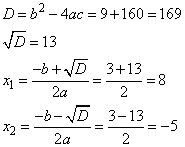
Из двух корней только второй 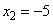 принадлежит ОДЗ.
принадлежит ОДЗ.
Ответ: -5.
Задание 21. Решите уравнение  .
.
Решение.
Так как каждое из слагаемых всегда больше либо равно 0, то уравнение будет равно нулю только если оба слагаемых равны 0, то есть данное уравнение можно записать в виде следующей системы:

Упрощаем данные выражения, имеем:
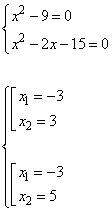
Имеем один общий корень -3, при котором оба уравнения одновременно равны 0, то есть этот корень есть решение уравнения.
Ответ: -3.
Задание 21. Решите уравнение 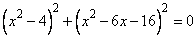 .
.
Решение.
Каждое из слагаемых уравнения всегда больше либо равно 0, следовательно, уравнение будет равно 0, только если оба слагаемых равны 0. Запишем это положение в следующем виде:

Упростим выражения, получим:
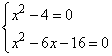
Первое уравнение дает два корня

Второе уравнение также дает два корня:
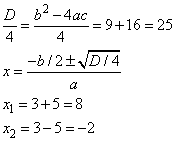
В результате получаем один общий корень 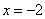 , при котором оба уравнения одновременно равны 0.
, при котором оба уравнения одновременно равны 0.
Ответ: -2.
Задание 21. Решите уравнение 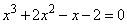 .
.
Решение.
Упростим выражение, запишем его в виде:
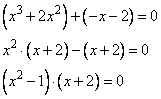
Последнее выражение будет равно 0, если хотя бы один из множителей равен 0, то есть имеем два уравнения:
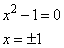
и
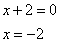
Таким образом, получили три корня уравнения -2; -1; 1.
Ответ: -2; -1; 1.
Задание 21. Решите уравнение 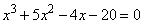 .
.
Решение.
Перепишем уравнение в следующем виде:
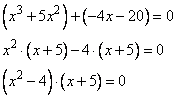
Последнее выражение будет равно 0, если хотя бы одна из скобок будет равна 0, то есть имеем следующие два уравнения:
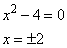
и
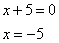
Таким образом, получили три корня уравнения -5; -2; 2.
Ответ: -5; -2; 2.
Задание 21. Найдите значение выражения 61a-11b+50, если 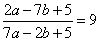 .
.
Решение.
Упростим выражение 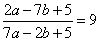 , перепишем его в следующем виде:
, перепишем его в следующем виде:

Чтобы привести выражение к виду 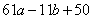 , прибавим к левой и правой части уравнения 10, получим:
, прибавим к левой и правой части уравнения 10, получим:
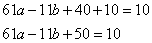
То есть получили значение 10.
Задание 21. Найдите значение выражения 39a-15b+25, если 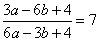 .
.
Решение.
Преобразуем выражение 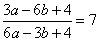 к виду
к виду

Чтобы получить выражение вида  прибавим к левой и правой части уравнения 1, получим:
прибавим к левой и правой части уравнения 1, получим:
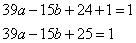
Ответ: 1.
Задание 21. Решите уравнение 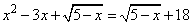 .
.
Решение.
1. Запишем ОДЗ уравнения
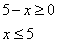
2. Упростим уравнение, получим:
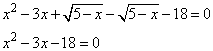
Решаем квадратное уравнение, имеем два корня:
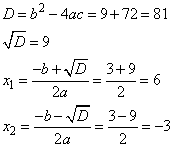
ОДЗ удовлетворяет только один корень -3.
Ответ: -3.
Задание 21. Решите уравнение 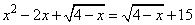 .
.
Решение.
1. ОДЗ уравнения
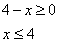
2. Упростим уравнение, получим:
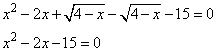
Решаем квадратное уравнение, имеем два корня:

ОДЗ принадлежит только один корень уравнения -3.
Ответ: -3.
Задание 21. Найдите значение выражения 19a-7b+12, если 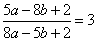 .
.
Решение.
Перепишем выражение 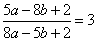 в виде:
в виде:

Приведем последнее выражение к виду 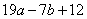 , получим:
, получим:
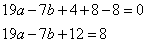
Ответ: 8.
Задание 21. Найдите значение выражения 25a-5b+22, если 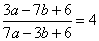 .
.
Решение.
Упростим выражение 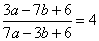 , получим:
, получим:
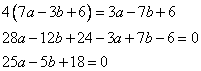
Чтобы привести последнее выражение к виду 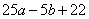 , добавим к выражению 4:
, добавим к выражению 4:
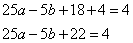
Ответ: 4.








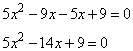
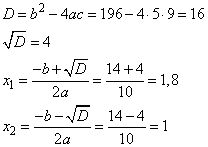
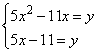
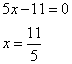
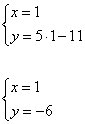 и
и 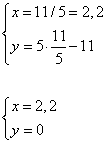
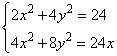
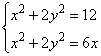
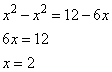
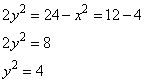
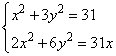
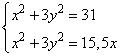
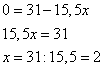
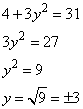
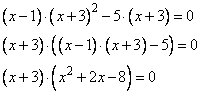
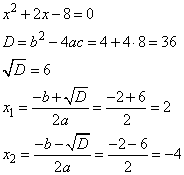
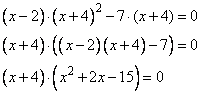
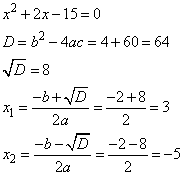
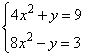
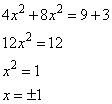
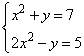
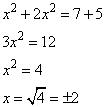
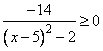 .
.
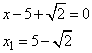 и
и