Разбор заданий по ОГЭ

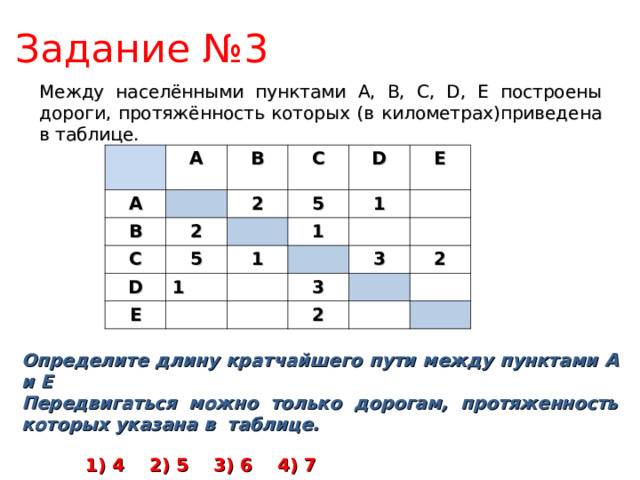
Задание № 3

Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах)приведена в таблице.

A

A

B

B

2

C

2

C

5

5

D

D

1

1

1

1

E

E

3

3

2

2

Определите длину кратчайшего пути между пунктами A и Е

Передвигаться можно только дорогам, протяженность которых указана в таблице.

1) 4 2) 5 3) 6 4) 7

A

A

B

B

C

5

C

5

D

D

E

E

6

9

3

3

8

8

4

4

2

2

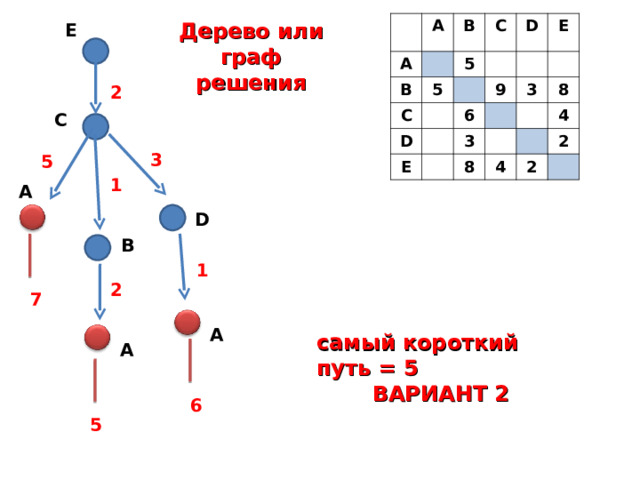
Дерево или граф

решения

Е

2

С

3

5

1

А

D

В

1

2

7

А

самый короткий путь = 5

ВАРИАНТ 2

А

6

5

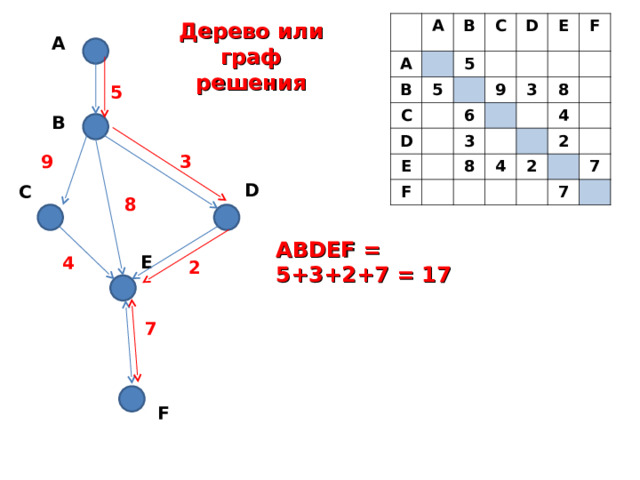
Задание № 3

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

A

A

B

B

C

5

5

C

D

D

E

9

E

6

3

3

F

F

8

8

4

4

2

2

7

7

Определите длину кратчайшего пути между пунктами A и F (при условии,

что передвигаться можно только по построенным дорогам).

1) 11 2) 13 3) 15 4) 17

A

A

B

B

5

C

5

C

D

D

E

E

9

6

F

F

3

3

8

8

4

4

2

2

7

7

Дерево или граф

решения

A

5

B

3

9

D

C

8

ABDEF = 5+3+2+7 = 17

E

4

2

7

F

A

A

B

B

C

5

C

5

D

D

6

E

E

9

F

3

3

F

8

8

4

4

2

2

7

7

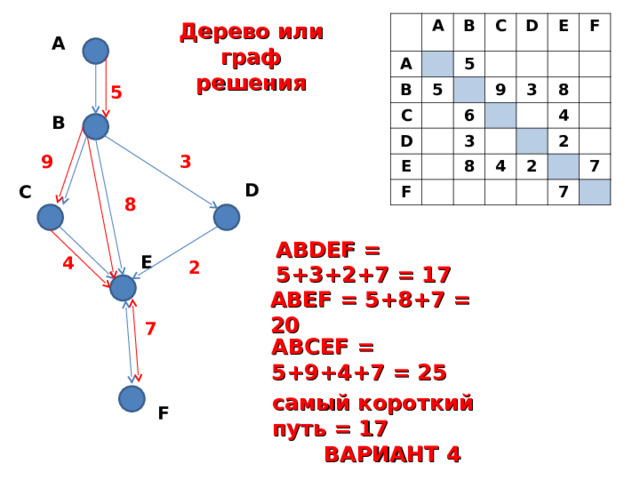
Дерево или граф

решения

A

5

B

3

9

D

C

8

ABDEF = 5+3+2+7 = 17

E

4

2

ABEF = 5+8+7 = 20

7

ABCEF = 5+9+4+7 = 25

самый короткий путь = 17

ВАРИАНТ 4

F

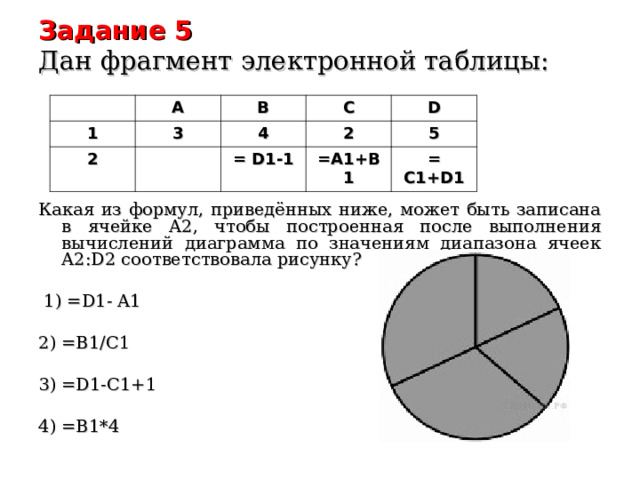
Задание 5 Дан фрагмент электронной таблицы:

Какая из формул, приведённых ниже, может быть записана в ячейке A2, чтобы постро­енная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 со­ответствовала рисунку?

1) =D1- A1

2) =В1/С1

3) =D1-C1+1

4) =В1*4

1

А

В

3

2

С

4

D

2

= D1-1

5

=A1+B1

= C1+D1

Дан фрагмент электронной таблицы .

После выполнения вычислений была построена диаграмма по значениям диапазона ячеек B1:B4. Укажите, какое число должно быть записано в ячейке A3, чтобы диаграмма соответствовала рисунку.

1) 1 2) 2 3) 3 4) 4

A

1

B

5

2

4

=A2/2

3

=A1–A2

4

6

=A4–A1

=A3*2

Задание 6

Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на ( a , b ) , где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a; y + b). Например, если Чертёжник находится в точке с координатами (9,5), то команда Сместиться на (1,-2)переместит Чертежник в точку (10, 3)

Запись

Повтори k раз

Команда1 Команда2 Команда3

конец

• Запись Повтори k раз Команда1 Команда2 Команда3 конец

означает, что последовательность команд Команда1 Команда2 Команда3 повторится k раз.

Чертёжнику был дан для исполнения следующий алгоритм:

ПОВТОРИ 3 РАЗ

сместиться на (-2, -3) сместиться на (3, 2) сместиться на (-4, 0)

КОНЕЦ

На какую одну команду можно заменить этот алгоритм, чтобы

Чертежник оказался в той же точке, что и после выполнения алгоритма?

• запишем общее изменение координат Чертёжника в результате выполнения этого алгоритма:

Задание 9  

Запишите значение переменной s, полученное в результате работы следующей программы. Текст программы приведён на трёх языках программирования.

Алгоритмический язык

Бейсик

алг

нач

цел s, k

s := 0

нц для k от 3 до 7

s := s + 6

кц

вывод s

кон

Паскаль

DIM k, s AS INTEGER

s = 0

FOR к = 3 TO 7

s = s + 6

NEXT k

PRINT s

Var s, k: integer;

Begin

s := 0;

for k := 3 to 7 do

s := s + 6;

writeln(s);

End.

Пояснение.

Цикл «for k := 3 to 7 do» выполняется пять раз. Каждый раз переменная s увеличивается на 6. Поскольку изначально s = 0, после выполнения программы получим: s = 5 · 6 = 30.

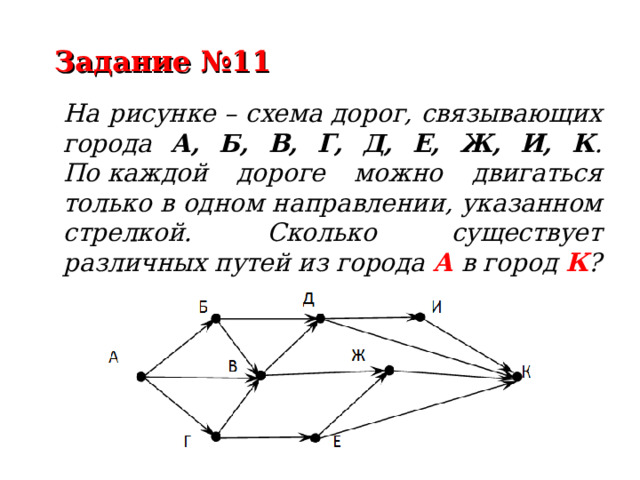
Задание №11

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К . По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К ?

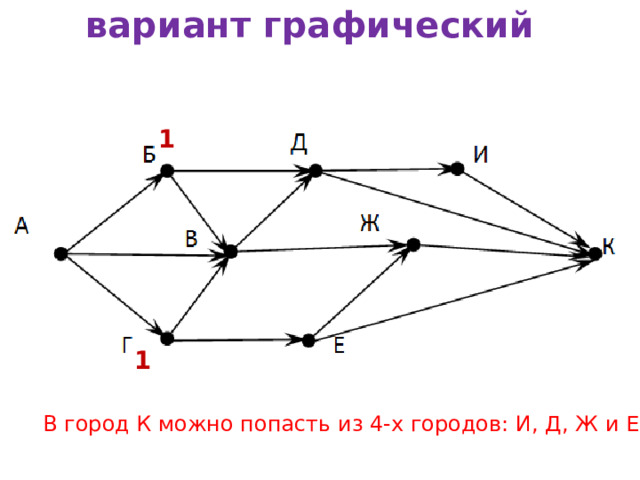
вариант графический

1

1

В город К можно попасть из 4-х городов: И, Д, Ж и Е.

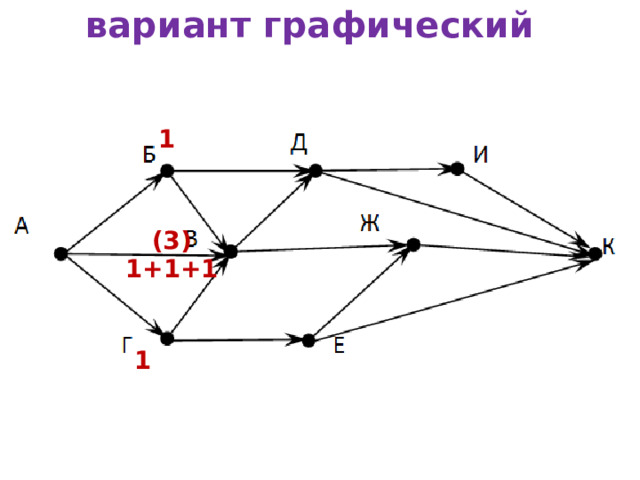
вариант графический

1

(3)

1+1+1

1

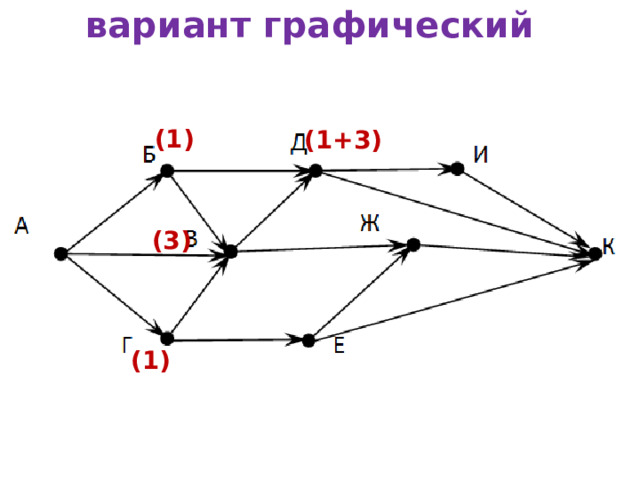
вариант графический

(1)

(1+3)

(3)

(1)

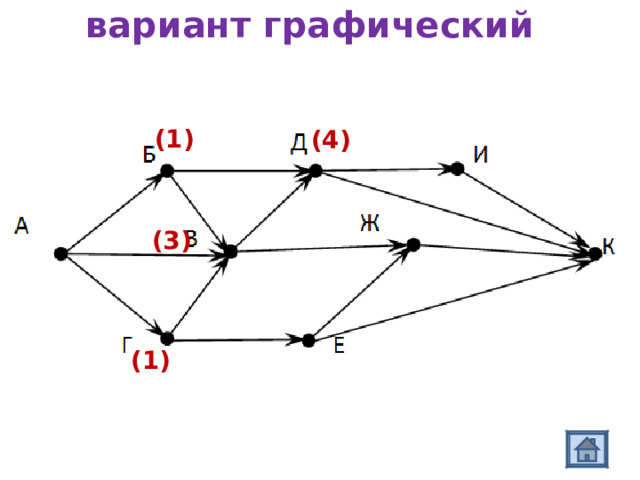
вариант графический

(1)

(4)

(3)

(1)

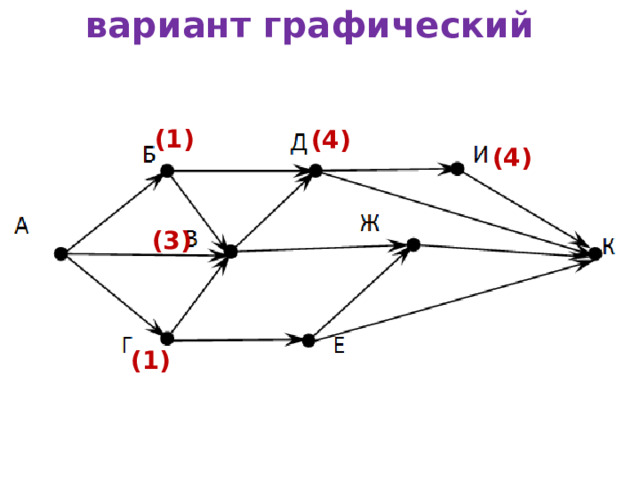
вариант графический

(1)

(4)

(4)

(3)

(1)

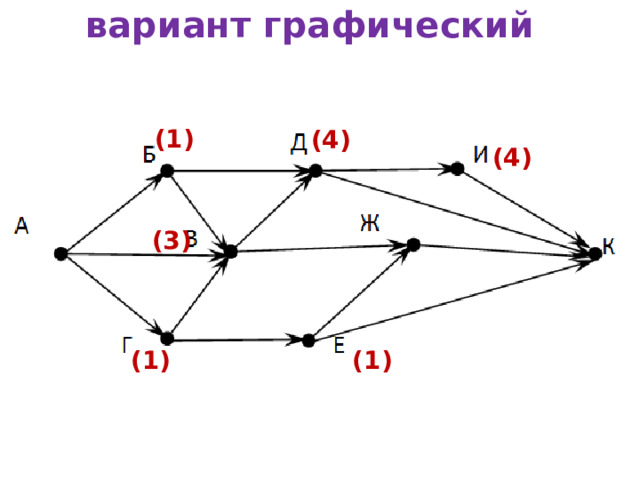
вариант графический

(1)

(4)

(4)

(3)

(1)

(1)

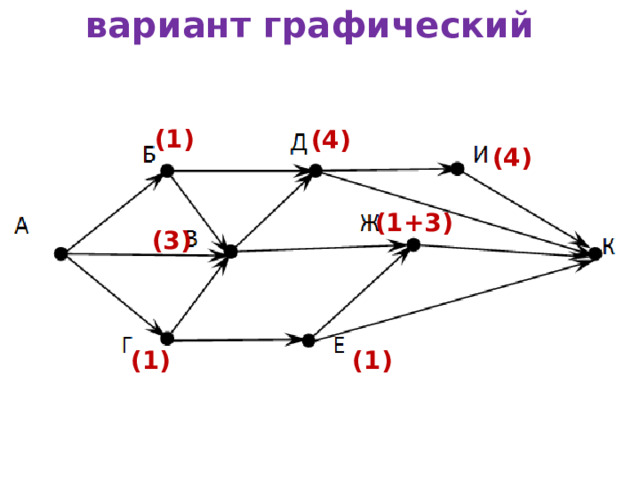
вариант графический

(1)

(4)

(4)

(1+3)

(3)

(1)

(1)

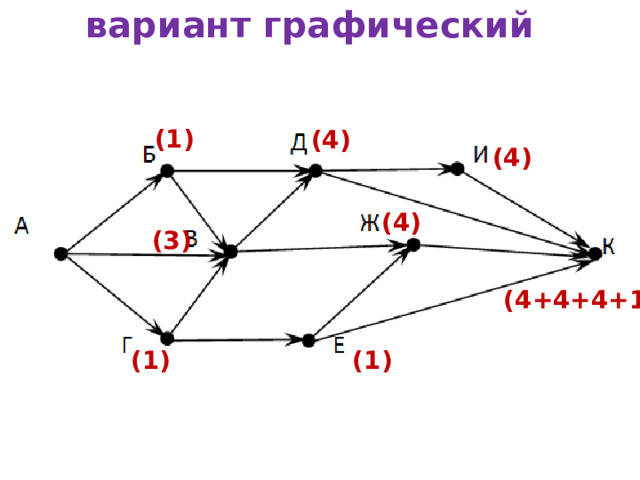
вариант графический

(1)

(4)

(4)

(4)

(3)

(4+4+4+1)

(1)

(1)

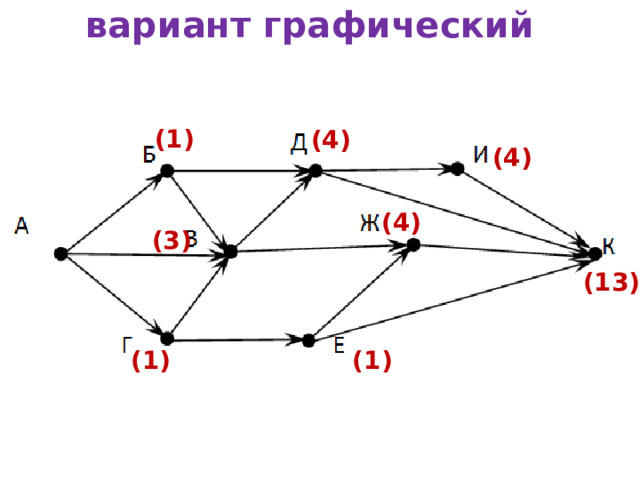
вариант графический

(1)

(4)

(4)

(4)

(3)

(13)

(1)

(1)

Задание №16

Автомат получает на вход трёхзначное десятичное число. По полученному числу строится новое десятичное число по следующим правилам.

1. Вычисляются два числа – сумма старшего и среднего разрядов, а также сумма среднего и младшего разрядов заданного числа.

2. Полученные два числа записываются друг за другом в порядке невозрастания (без разделителей).

Пример. Исходное число: 277. Поразрядные суммы: 9, 14. Результат: 149.

Определите, сколько из приведённых ниже чисел могут получиться в результате работы автомата.

1616 169 163 1916 1619 316 916 116

В ответе запишите только количество чисел.

Решение: Не забывая о том, что максимальная сумма разрядов 9+9=18, исключаем варианты 1916, 1619;

Порядок невозрастания (большее число стоит перед меньшим), исключаем 316, 916

Остались варианты: 1616, 169, 163, 116- четыре варианта

Ответ: 4

Задание №16

Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Сначала записывается исходная цепочка символов, после нее записывается исходная цепочка символов в обратном порядке, затем записывается буква, следующая в русском алфавите за той буквой, которая в исходной цепочке стояла на последнем месте. Получившаяся цепочка является результатом работы алгоритма.

Например, если исходная цепочка символов была ЛЕС, то результатом работы алгоритма будет цепочка ЛЕССЕЛТ.

Дана цепочка символов ЕН . Какая цепочка символов получится, если к данной цепочке применить алгоритм дважды (то есть к данной цепочке применить алгоритм, а затем к результату его работы еще раз применить алгоритм)?

Русский алфавит:

АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ

Решение: ЕН – ЕННЕ-ЕННЕО-(второй раз)-ЕННЕООЕННЕ-

ЕННЕООЕННЕП

Ответ: ЕННЕООННЕП

Некоторый алгоритм из одного числа получает новое число следующим образом. Исходное число записывается дважды (друг за другом), а в конец получившегося числа дописывается столько нулей, сколько четных цифр в исходном числе. Получившееся число является результатом работы алгоритма.

Например, если исходное число было 325, то результатом работы алгоритма будет число 3253250.

Дано число 144 . Сколько нулей будет содержаться в итоговом числе, если к исходному числу применить описанный алгоритм дважды (т.е. применить алгоритм к данному числу, а затем к результату вновь применить алгоритм)?

Решение:

144-144144 (количество четных цифр в исходном числе 2)

14414400-(второй раз)-1441440014414400 (количество четных цифр 4)-14414400144144000000- итого: 8 нулей

Ответ: 8