Разбор заданий школьного этапа ВсШО по математике для 7 класса

1. класс (решения)

Задача 7.1. На картинке нарисованы девять квадратиков, на восьми из них нарисованы стрелки. Числа 1 и 9 в них уже расставлены. Замените буквы в оставшихся квадратиках на числа от 2 до 8 так, чтобы стрелки квадратика с числом 1 указывали в направлении квадратика с числом 2 (число 2 может быть в квадратике 𝐴 или 𝐵), стрелки квадратика с числом 2 указывали в направлении квадратика с числом 3 и т. д., стрелки квадратика с числом 8 указывали в направлении квадратика с числом 9).

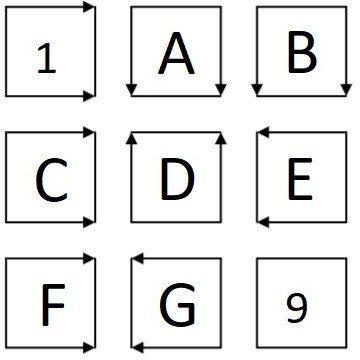
Постройте соответствие.

• В квадрате 𝐴

• В квадрате 𝐵

• В квадрате 𝐶

• В квадрате 𝐷

• В квадрате 𝐸

• В квадрате 𝐹

• В квадрате 𝐺

• стоит число 2.

• стоит число 3.

• стоит число 4.

• стоит число 5.

• стоит число 6.

• стоит число 7.

• стоит число 8.

Ответ: В квадрате 𝐴 стоит число 6, в 𝐵 – 2, в 𝐶 – 4, в 𝐷 – 5, в 𝐸 – 3, в 𝐹 – 8, в 𝐺 – 7.

Решение. Упорядочим все квадратики по возрастанию чисел в них. В этой «возрастаю- щей цепочке» содержатся все девять квадратиков.

Заметим, что в этой цепочке непосредственно перед 𝐶 может быть только 𝐸 (на 𝐶 ничего не указывает, кроме стрелок 𝐸). Аналогично, непосредственно перед 𝐸 может быть только

𝐵 (не 𝐶, потому что 𝐶 находится после 𝐸). Непосредственно перед 𝐵 может быть только

1. Следовательно, в квадратиках 𝐵, 𝐸, 𝐶 стоят числа 2, 3, 4 соответственно. Тогда 5 стоит точно в 𝐷, 6 стоит точно в 𝐴, 7 стоит точно в 𝐺, 8 стоит точно в 𝐹.

Задача 7.2. Петя купил себе в магазине шорты для футбола.

• Если бы он купил шорты с футболкой, стоимость покупки была бы вдвое больше.

• Если бы он купил шорты с бутсами, стоимость покупки была бы впятеро больше.

• Если бы он купил шорты с щитками, стоимость покупки была бы втрое больше.

Во сколько раз больше была бы стоимость покупки, если бы Петя купил шорты, футболку, бутсы и щитки?

Ответ: 8.

Решение. Пусть шорты стоили 𝑥. Поскольку шорты с футболкой стоят 2𝑥, то футболка стоит тоже 𝑥. Поскольку шорты с бутсами стоят 5𝑥, то бутсы стоят 4𝑥. Поскольку шорты с щитками стоят 3𝑥, то щитки стоят 2𝑥. Тогда если бы Петя купил шорты, футболку, бутсы и щитки, то его покупка составила бы 𝑥 + 𝑥 + 4𝑥 + 2𝑥 = 8𝑥, что в 8 раз больше, чем 𝑥.

Задача 7.3. Лёша собирал друзей поиграть в прятки. Он опросил Андрея, Борю, Васю, Гену и Дениса и узнал следующее.

• Если Андрей пойдёт играть в прятки, то Боря тоже пойдёт, а Вася — нет.

• Если Боря пойдёт играть в прятки, то Гена или Денис тоже пойдёт.

• Если Вася не пойдёт играть в прятки, то Боря и Денис тоже не пойдут.

• Если Андрей не пойдёт играть в прятки, то Боря пойдёт играть, а Гена не пойдёт.

В итоге Лёша с кем-то из друзей сыграл в прятки. С кем именно? (Все ребята придержи- вались своих мнений.)

Ответ: С Борей, Васей и Денисом.

Решение. Вне зависимости от того, пойдёт ли Андрей играть в прятки, Боря пойдёт точ- но. Тогда и Вася пойдёт играть в прятки (если бы Вася не пошёл, то не пошёл бы и Боря). Тогда Андрей не пойдёт играть в прятки (если бы Андрей пошёл, то не пошёл бы Вася). Тогда Гена точно не пойдёт. Поскольку Боря пойдёт, пойдёт также Гена или Денис. По- скольку Гена не пойдёт, то пойдёт Денис. Итак, в прятки с Лёшей сыграли только Боря, Вася и Денис.

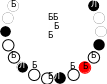
Задача 7.4. По кругу стоят семь шкатулок, в каждой из них лежит несколько монет. На рисунке изображено, сколько монет в какой шкатулке лежит.

За один ход разрешается переложить одну монету в соседнюю шкатулку. Какое мини- мальное количество ходов потребуется, чтобы уравнять количество монет во всех шка- тулках?

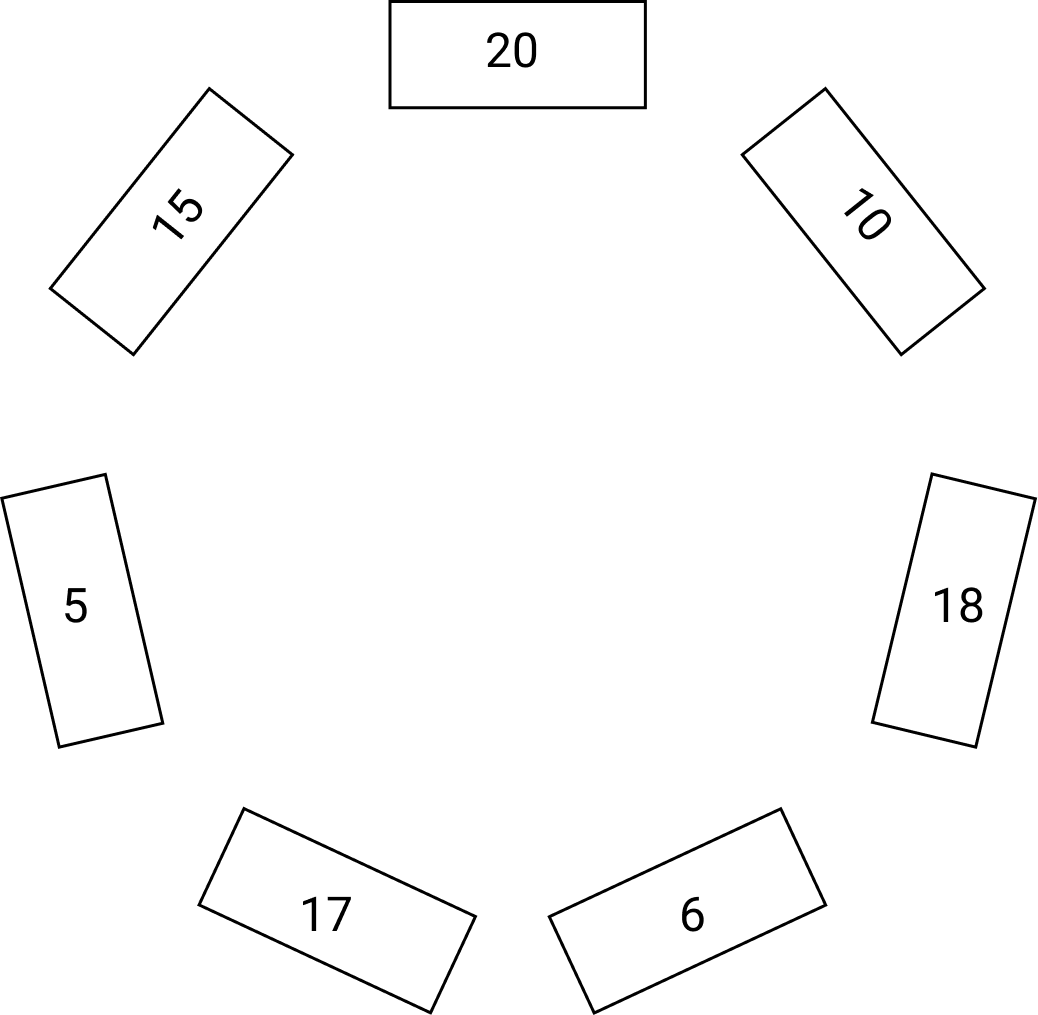
Ответ: 22.

Решение. Заметим, что всего монет суммарно 91, поэтому после всех ходов в каждой шка- тулке должно получиться ровно по 13 монет. Из шкатулки с 20 монетами нужно перело-

жить хотя бы 7 монет. Теперь рассмотрим шкатулки, соседние со шкатулкой с 20 моне- тами. Изначально в них суммарно 25 монет, и ещё хотя бы 7 монет в них перейдёт из шкатулки с 20 монетами. В итоге в этих двух шкатулках должно получиться суммарно 26 монет, поэтому хотя бы 25 + 7 − 26 = 6 монет нужно будет из этих шкатулок переложить. Осталось рассмотреть шкатулки с 17 и 18 монетами, из них нужно переложить хотя бы 4 и 5 монет соответственно. Итого ходов должно быть хотя бы 7 + 6 + 4 + 5 = 22.

Приведём пример, как уравнять все шкатулки ровно за 22 хода. Из шкатулки с 20 моне- тами перекладываем 3 монеты в шкатулку с 10 (там становится 13), а также 4 монеты в шкатулку с 15 (там становится 19). Из шкатулки, где стало 19 монет, перекладываем 6 монет в шкатулку с 5 монетами (там становится 11). Из шкатулки с 17 монетами пере- кладываем 2 монеты в шкатулку с 11, а также 2 монеты в шкатулку с 6 (там становится 8). Осталось переложить 5 монет из шкатулки с 18 монетами в шкатулку с 8 монетами. Итого во всех шкатулках стало ровно по 13 монет. Несложно убедиться в том, что было сделано ровно 22 хода.

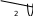
Задача 7.5. Прямоугольную полоску длины 16 разрезали на две полоски длин 9 и 7. Эти две полоски положили на стол так, как показано на рисунке.

Известно, что площадь части стола, покрытой только левой полоской, равна 27, а пло- щадь части стола, покрытой только правой полоской, равна 18. Найдите площадь части стола, покрытой обеими полосками.

Ответ: 13,5.

Решение. Поскольку у двух получившихся полосок ширина одинакова, их площади отно- сятся как их длины, т.е. 9 ∶ 7. Обозначим через 𝑆 площадь, покрытую обеими полосками. Тогда ^{27 + 𝑆} = ⁹ , откуда получаем 7 ⋅ (27 +𝑆) = 9 ⋅ (18 +𝑆). Решая это линейное уравнение,

18 + 𝑆 7

получаем 𝑆 = 13, 5.

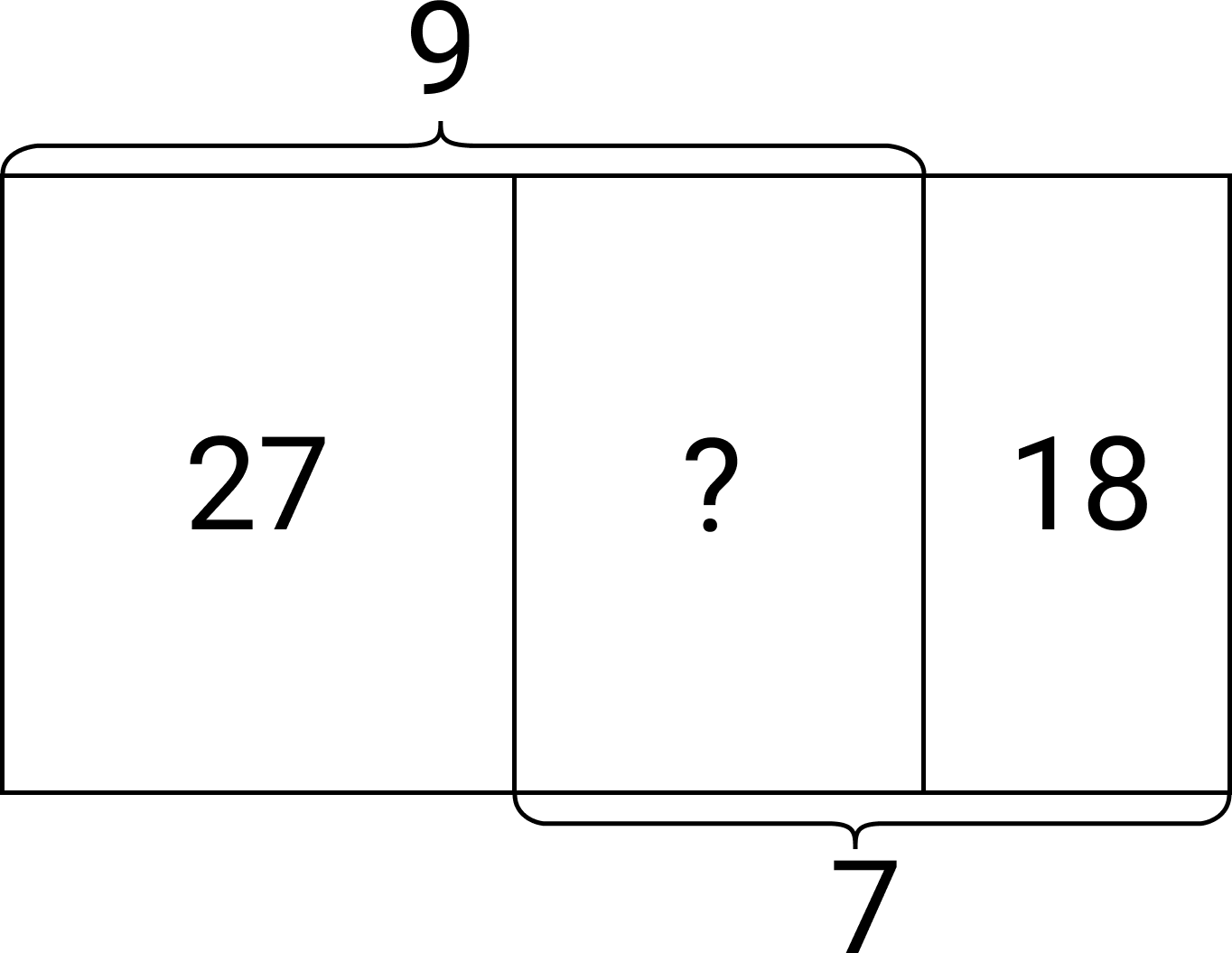
Задача 7.6. На инженерном калькуляторе цифры отображаются так, как показано на ри- сунке ниже.

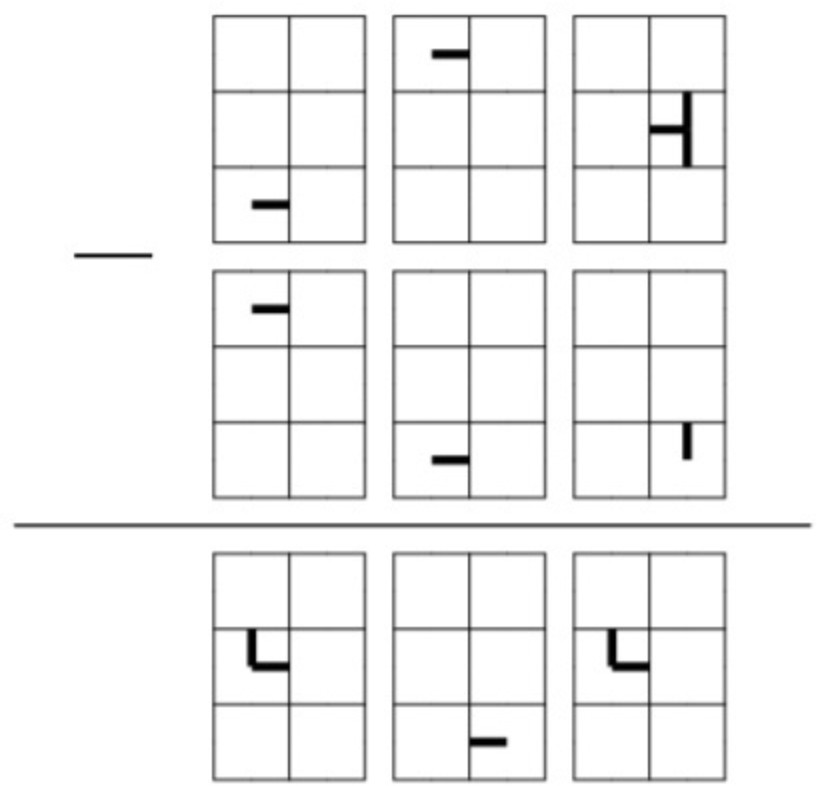
Дима на калькуляторе вычел из трёхзначного числа трёхзначное число и получил трёх- значное число. Но у калькулятора сломался экран, поэтому пример выглядел так, как показано на следующем рисунке. (В каждом прямоугольнике, состоящем из шести квад- ратиков, находится какая-то цифра. Среди этих шести квадратиков полностью исправно работает только один, на остальных пяти не отображается ничего.)

Чему в примере должны равняться уменьшаемое и вычитаемое, чтобы разность прини- мала наибольшее возможное значение? (Ответы можно вводить в любом порядке.)

Ответ: Уменьшаемое равно 923, вычитаемое равно 394.

Решение. Пусть 𝑎𝑏𝑐 — верхнее число, 𝑑𝑒𝑓 — среднее число, 𝑔ℎ𝑖 — нижнее число (разным буквам могут соответствовать одинаковые цифры). Последовательно сравнивая фрагмен- ты цифр с полноценными изображениями, получаем варианты того, где какая цифра может быть. А именно, 𝑎 ∈ {3, 5, 9}, 𝑏 ∈ {2, 3, 7}, 𝑐 ∈ {3, 4, 8, 9}, 𝑑 ∈ {2, 3, 7}, 𝑒 ∈ {3, 5, 9},

𝑓 ∈ {1, 4, 7}, 𝑔 ∈ {4, 5, 9}, ℎ ∈ {2}, 𝑖 ∈ {4, 5, 9}.

Заметим, что 𝑔ℎ𝑖 = 𝑎𝑏𝑐 −𝑑𝑒𝑓 , поэтому 𝑔 . Следовательно, 𝑔ℎ𝑖 ⩽ 529. Предположим, что разность 529 возможна, т.е. 𝑎𝑏𝑐 − 𝑑𝑒𝑓 = 529 или

𝑎𝑏𝑐 = 𝑑𝑒𝑓 + 529.

Поскольку 𝑎𝑏𝑐 = 𝑑𝑒𝑓 + 529 ⩾ 100 + 529 = 629, то 𝑎 ⩾ 6, т.е. 𝑎 = 9. Если 𝑑 = 2, то 900 ⩽ 𝑎𝑏𝑐 = 2𝑒𝑓 + 529 — противоречие. Если 𝑑 = 7, то 1000 𝑎𝑏𝑐 = 7𝑒𝑓 + 529 ⩾ 700 + 529 1000 — противоречие. Значит, 𝑑 = 3.

Рассмотрев разряд единиц, получаем, что сумма 𝑓 + 9 оканчивается на цифру 𝑐. Если

𝑓 = 1, то 𝑐 = 0 — противоречие. Если 𝑓 = 7, то 𝑐 = 6 — противоречие. Остался только случай 𝑓 = 4, тогда 𝑐 = 3.

Если 𝑒 ⩽ 5, то 900 ⩽ 𝑎𝑏𝑐 = 3𝑒4 + 529 ⩽ 354 + 529 900 — противоречие. Значит, 𝑒 5, т.е.

𝑒 = 9. Тогда 𝑎𝑏𝑐 = 394 + 529 = 923, и 𝑏 = 2.

Итак, наибольшая возможная разность достигается только в случае 923 − 394 = 529.

Задача 7.7. По кругу высажено 130 деревьев: берёзы и липы (оба вида присутствуют). На каждом дереве висит табличка с надписью: «Рядом растут два разных дерева». Извест- но, что среди всех деревьев неправда написана на всех липах и ровно на одной берёзе. Сколько могло быть высажено берёз? Укажите все возможные варианты.

Ответ: 87.

Решение. Разобьём все деревья на чередующиеся группы подряд идущих берёз и подряд идущих лип (по условию есть группы обоих видов).

Предположим, существует группа из хотя бы 2 лип. Тогда на крайней из них была бы написана правда (ведь она находится между берёзой и липой) — противоречие. Значит, все группы лип состоят из 1 дерева. Тогда каждая липа находится между двумя берёзами, и на ней действительно написана неправда.

Рассмотрим теперь, какие могут быть по количеству группы берёз.

• Если в группе хотя бы 4 берёзы, то на всех некрайних (хотя бы на двух) написана неправда (ведь каждая из них находится между двумя берёзами) — противоречие, ведь таких берёз по условию всего одна.

• Если в группе 3 берёзы, то только на средней из них написана неправда.

• Если в группе 2 берёзы, то на каждой из них написана правда.

• Если в группе 1 берёза, то на ней написана неправда (ведь она находится между двумя липами).

Следовательно, существует несколько групп по 2 берёзы и ровно одна группа из 1 или 3

берёз.

Если есть группа из 1 берёзы, временно забудем её и одну соседнюю с ней липу. Тогда оставшиеся 130 − 2 = 128 деревьев разобьются на блоки из 3 деревьев: двух берёз и одной липы. Но 128 не делится на 3 — противоречие.

3

Задача 7.8. У короля и королевы было три сына и несколько дочерей (хотя бы одна). 1-го сентября некоторого года король и королева заметили, что им обоим по 35 лет, более того,

суммарный возраст их детей составляет тоже 35 лет. А 1-го сентября несколько лет спустя король и королева заметили, что их суммарный возраст равен суммарному возрасту всех их детей. (Новых детей за это время не появлялось; никто из членов семьи за это время не умер.)

Сколько детей у королевской четы, если известно, что их не больше 20? Укажите все воз- можные варианты.

Ответ: 7 или 9.

Решение. Пусть у короля и королевы было 𝑑 ⩾ 1 дочерей. Пусть также между двумя опи- санными моментами времени прошло 𝑛 лет.

Изначально разность суммарного возраста родителей и суммарного возраста детей рав- нялась 35 + 35 − 35 = 35 лет, а через 𝑛 лет она стала равна 0. Поскольку каждый год эта разность уменьшалась на (𝑑 + 3) − 2 = 𝑑 + 1 лет (ведь на 1 год становится старше каждый из 𝑑 + 3 детей и каждый из 2 родителей), то

35 = 𝑛(𝑑 + 1).

Число 35 представимо в виде произведения двух натуральных чисел 𝑛 и 𝑑+1 ⩾ 2, поэтому остаётся рассмотреть только три случая.

Пусть 𝑛 = 1, 𝑑 + 1 = 35. Тогда 𝑑 = 34 — получаем противоречие с тем, что всего детей не больше 20.

Пусть 𝑛 = 7, 𝑑 + 1 = 5. Тогда 𝑑 = 4, и всего детей было 4 + 3 = 7. Такой случай возможен, например, если в семье в первый момент времени трём сыновьям было 2, 3, 4 года, а че- тырём дочерям было 5, 6, 7, 8 лет. Тогда суммарно детям было 2 + 3 + 4 + 5 + 6 + 7 + 8 = 35 лет — столько же, сколько королю и королеве. А через 7 лет им суммарно стало 9 + 10 + 11 + 12 + 13 + 14 + 15 = 84 = 42 + 42 — столько же, сколько суммарно королю и королеве.

Пусть 𝑛 = 5, 𝑑 + 1 = 7. Тогда 𝑑 = 6, и всего детей было 6 + 3 = 9. Такой случай возможен, например, если в семье в первый момент времени трём сыновьям было 1, 2, 4 года, а ше- сти дочерям было 1, 2, 4, 6, 7, 8 лет. Тогда суммарно детям было 1 + 2 + 4 + 1 + 2 + 4 + 6 + 7 + 8 = 35 лет — столько же, сколько королю и королеве. А через 5 лет им суммарно стало 6 + 7 + 9 + 6 + 7 + 9 + 11 + 12 + 13 = 80 = 40 + 40 — столько же, сколько суммарно королю и королеве.