Различные способы разложения многочлена на множители

Муниципальное бюджетное образовательное учреждение Краснинская средняя общеобразовательная школа

Различные

способы

разложения

многочлена

на множители

Работу выполнил Климов Никита

7а класс

Руководитель: Серова Надежда Николаевна

Красный 2015

Цели : изучить различные способы разложения многочлена на множители.

Задачи:

• Познакомиться с литературой по этой теме
• Научиться применять способы разложения на множители при решении задач
• Самостоятельно решить несколько олимпиадных задач по названной теме
• Выступить перед учащимися 7 класса

• Методы исследования

• Анализ математической литературы по теме исследования
• Изучение, исследование и сбор информации
• Решение задач по теме

• Гипотеза:

«Мало иметь хороший ум, главное – уметь его применять» Р. Декарт

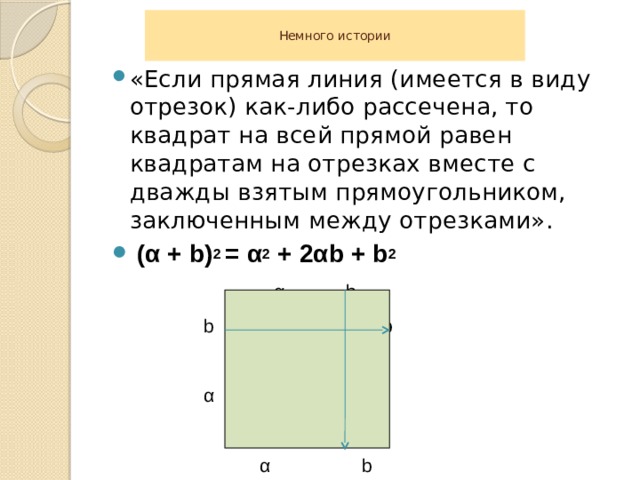
Немного истории

• «Если прямая линия (имеется в виду отрезок) как-либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольником, заключенным между отрезками».
• (α + b) 2 = α 2 + 2αb + b 2

α b

b b

α α

α b

Основные способы разложения многочлена на множители

• Вынесение общего множителя за скобки
• Способ группировки
• Применение формул сокращенного умножения
• Комбинация различных приемов

• Метод выделения полного квадрата Метод введения новой переменной
• Метод выделения полного квадрата Метод введения новой переменной
• Метод выделения полного квадрата
• Метод введения новой переменной

Основные способы разложения многочлена на множители

• Вынесение общего множителя за скобки

Алгоритм отыскания общего множителя нескольких одночленов

• Найти наибольший общий делитель коэффициентов всех членов многочлена – это общий числовой множитель (коэффициент)
• Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
• Произведение коэффициента, найденного на первом шаге, и степеней, найденных на втором шаге, является общим множителем, который нужно вынести за скобки

Основные способы разложения многочлена на множители

1) Вынесение общего множителя за скобки

• Примеры :
• 12ху 4 – 18сх 2 у 3 = 6ху 3 (2у – 3сх).
• 2,4х + 7,2у = 2,4(х + 3у);
• 2х (х – 2) + 5 (х – 2) 2 = (х – 2) (2х + 5(х – 2)) = =(х – 2)(2х + 5х – 10) = (х – 2)(7х – 10).

Основные способы разложения многочлена на множители

2) Способ группировки

Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде групп одинакового количества слагаемых таким образом, чтобы из каждой группы можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.

Основные способы разложения многочлена на множители

2) Способ группировки

• Пример 1 . Разложить на множители многочлен 2х 2 + 6х + ху + 3у.
• Решение . 2х 2 + 6х + ху + 3у=(2х 2 + 6х) + (ху + 3у)=

=2х(х + 3) + у(х + 3)= (х + 3)(2х + у).

• Пример 2 . Разложить на множители многочлен αb 2 – 2αb + 3α + 2b 2 – 4b + 6.
• Решение: αb 2 – 2αb + 3α + 2b 2 – 4b + 6 = =(αb 2 + 2b 2 ) – (2αb + 4b)+ (3α + 6)=

=b 2 (α + 2) – 2b(α + 2)+3 (α + 2)= (α + 2)(b 2 – 2b+3).

• Пример 3. Разложить на множители многочлен

х 2 – 7х + 12.

• Решение: . х 2 – 7х + 12 = х 2 – 3х – 4х + 12 =

=х(х – 3) – 4(х – 3)= (х – 3)(х – 4).

Основные способы разложения многочлена на множители

3) Применение формул сокращенного умножения

• α 2 – b 2 = (α – b) (α + b) (1)
• α 3 – b 3 = (α – b) (α 2 + αb + b 2 ) (2)
• α 3 + b 3 = (α + b) (α 2 – αb + b 2 ) (3)
• α 2 + 2αb + b 2 = (α + b) 2 (4)
• α 2 – 2αb + b 2 = (α – b) 2 (5)
• α 3 + 3α 2 b + 3αb 2 + b 3 = (α+b) 3 (6)
• α 3 – 3α 2 b + 3αb 2 – b 3 = (α – b) 3 (7)

Основные способы разложения многочлена на множители

3) Применение формул сокращенного умножения

• Пример 4 . Разложить на множители многочлен х 4 - 1.

•   Решение:  x  4  – 1 = ( x  2  )  2  – 1  2  = ( x  2  – 1)( x  2  + 1) =

= ( x  2  – 1  2  )( x  2  + 1) = ( x + 1)( x – 1)( x  2  +1).

• Пример 5. Разложить на множители многочлен 

x  4  + 4 x  2  – 5.

•   Решение . x  4  + 4 x  2  – 5= x  4  + 4 x  2 +4 – 9=(x  2 +2) 2 – 9=

=(x  2 +2 – 3) (x  2 +2 +3)=(x  2 –1)(x  2 +5)=(х – 1)(х+1)(x  2 +5)

• Пример 6 . Разложим на множители многочлен х 6  – 1.
• Решение . х 6  – 1= (х 3 ) 2  – 1 = (х 3  + 1) ∙ (х 3  – 1)= =(х 3  + 1) ∙ (х 3  – 1) = (х + 1) ∙ (х 2  – х + 1) ∙ (х – 1) ∙ (х 2  + х + 1).

Основные способы разложения многочлена на множители

4) Комбинация различных приёмов

• Метод выделения полного квадрата

• Пример 7. Разложить на множители многочлен

α 4 – 3α 2 + 1.

• Решение. α 4 – 3α 2 + 1=(α 4 – 2α 2 + 1) – α 2 =(α 2 – 1) 2 – α 2 =

=(α 2 – 1 – α)( α 2 – 1 +α)=(α 2 – α– 1)( α 2 +α– 1).

• Пример 8. Разложить на множители многочлен α 4 + 4.
• Решение. α 4 + 4 = (α 4 + 4α 2 + 4) – 4α 2 =(α 2 + 2) 2 – 4α 2 =

=(α 2 + 2 – 2α)( α 2 + 2 +2α)=(α 2 – 2α + 2)( α 2 +2α + 2).

• Пример 9. Разложить на множители многочлен х 5 – 1.
• Решение. х 5 – 1= х 5 – х 2 + х 2 –1= х 2 (х 3 – 1) + (х 2 –1) =
• = х 2 (х – 1)( х 2 + х + 1) + (х –1)(х + 1)=

=(х – 1)( х 2 ( х 2 + х + 1) + (х + 1)) = (х – 1)( х 4 + х 3 + х 2 + х + 1).

Основные способы разложения многочлена на множители

4) Комбинация различных приёмов

• Метод введения новой переменной

• Пример 10. Разложить на множители
• х(х + 1)(х + 2)(х + 3) – 15.
• Решение. х(х + 1)(х + 2)(х + 3) – 15 =

=( (х(х + 3))((х + 1)(х + 2)) ) – 15 =(х 2 + 3х) (х 2 + 3х +2)– 15 . Далее введем новую переменную. Обозначим

х 2 + 3х = α , тогда наше выражение примет новый вид (более простой):

• α(α + 2) –15 =α 2 + 2α –15 =α 2 + 2α + 1 – 16 = (α + 1) 2 – 16= =(α + 1 – 4)(α + 1 +4)= (α – 3)(α +5). Возвращаемся к исходной переменной, вместо α поставим х 2 +3х ,

получим

• х(х + 1)(х + 2)(х + 3) – 15 = (х 2 + 3х – 3)( х 2 + 3х +5) .

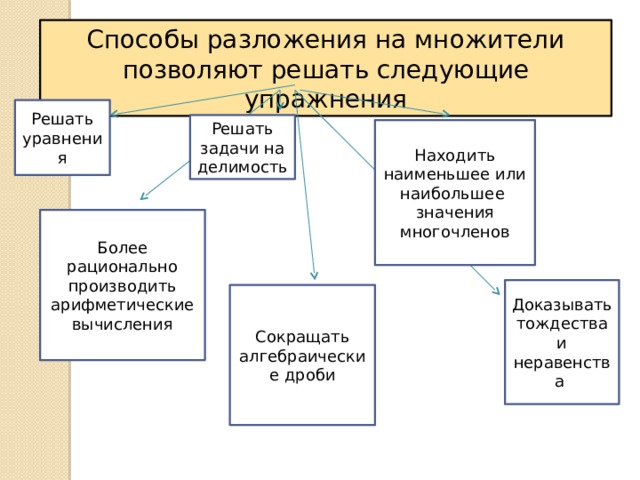
Способы разложения на множители позволяют решать следующие упражнения

Решать уравнения

Решать задачи на делимость

Находить наименьшее или наибольшее значения многочленов

Более рационально производить арифметические вычисления

Доказывать тождества и неравенства

Сокращать алгебраические дроби

Способы разложения на множители позволяют решать следующие упражнения

• Пример11 . Решить уравнение
• (х – 1) 3 = х 2 (х – 1).
• Решение . Перенесу члены уравнения в левую часть и разложу её на множители:

(х – 1) 3 = х 2 (х – 1) , (х – 1) 3 – х 2 (х – 1) = 0,

(х –1)((х – 1) 2 –х 2 )= 0,

(х –1)(х – 1 –х) (х –1 + х)= 0,

– (х –1) (2х – 1)=0, произведение множителей равно нулю, если один из них равен нулю. Получаю два линейных уравнения: х – 1 = 0 (корень х = 1) и 2х –1= 0 (корень х = 0,5).

• Ответ: 0,5 и 1.

Способы разложения на множители позволяют решать следующие упражнения

• Пример12. Доказать, что при всех натуральных n значение выражения

(3n +2) 3 + (4n + 5) 3 кратно 7.

• Решение. Применяю формулу суммы кубов:
• (3n +2) 3 + (4n + 5) 3 =

=(3n +2 + 4n + 5)( (3n +2) 2 - (3n + 2)(4n+5)+ +(4n +5) 2 )=

=(7n+7)( (3n +2) 2 - (3n + 2)(4n+5) +(4n + 5) 2 )=

=7(n+1)( (3n +2) 2 - (3n + 2)(4n+5) +(4n + 5) 2 ). Данное выражение имеет множитель 7,

• поэтому оно кратно 7.

Способы разложения на множители позволяют решать следующие упражнения

• Пример13. Сократить алгебраическую дробь

• Решение: Разложу числитель и знаменатель дроби на множители:

х 2 + 10х+24= х 2 + 10х+25 – 1=(х +5) 2 –1= (х+5 - 1)(х+5+1)= =(х+4)(х+6),

• х 2 – 36=(х – 6 )(х+6).

Способы разложения на множители позволяют решать следующие упражнения

• Пример14. Вычислить

• Решение. Применяю формулу разности квадратов:
• = = 0,44

Способы разложения на множители позволяют решать следующие упражнения

• Пример 15 Найти наименьшее значение выражения: α 2 + 6αb+10b 2 –2b+3. При каких значениях α и b оно достигается?
• Решение . Сгруппирую члены выражения и использую формулы квадрата суммы и разности . Получаю: α 2 + 6αb+10b 2 –2b+3=
• =(α 2 + 6αb+9b 2 )+( b 2 –2b+1)+2=(α+3b) 2 +(b – 1) 2 +2. Квадрат любого выражения неотрицателен, значит наименьшее значение данного выражения равно 2. Оно достигается при условии α+3b=0 и b –1=0, т.е. при b=1 и α= - 3b= - 3.
• Ответ: 2 при α= –3 и b=1.

Способы разложения на множители позволяют решать следующие упражнения

• Пример 16. Пример 13 .Доказать неравенство: х 2 +4х≥ - 4.
• Решение. Преобразую левую часть неравенства до полного квадрата:

х 2 +4х= х 2 +4х+4 – 4= (х+2) 2 – 4≥ - 4, т.к. (х+2) 2 ≥ 0. Что и требовалось доказать.

Решение олимпиадных задач

• Задача 1 . («Кенгуру»- 2014, 7-8 классы).Про числа х и у известно, что х≠у и (х –1) 2 + 3х=( у –1) 2 +3у. Чему равна сумма этих чисел?
• Решение. Раскрою скобки в левой и правой части, приведу подобные, перенесу всё в левую часть уравнения и разложу её на множители:

х 2 – 2х +1+3х= у 2 – 2у +1+3у, х 2 +х – у 2 –у=0, х 2 – у 2 +х –у=0,

(х –у)( х +у)+( х –у)=0, (х –у)( х +у+1)=0. х –у≠0, т.к. х≠у, значит

х +у+1=0, х+у = - 1.

• Ответ: - 1.
• Задача 2. ( пособие Э.Н.Балаян . «750 лучших олимпиадных и занимательных задач по математике.7-8 классы.». Ростов-на-Дону: «Феникс», 2014)

Разложить число 302 ∙ 324 + 121 на простые множители .

• Решение. Решается эта задача мгновенно: (313 - 11)(313 + 11)+121=

313 2 – 11 2 +121= 313 2 (313 – простое число).

k, то из чисел n – k и n+k+1 одно обязательно четное, значит А кратно 8. Задача 4 (олимпиады прошлых лет) Вычислить значение выражения Зх 4 +2у 4 + 5х 2 у 2 +у 2 , если х 2 +у 2 =1. Решение. Зх 4 +2у 4 + 5х 2 у 2 +у 2 = Зх 4 + 3х 2 у 2 +2х 2 у 2 +2у 4 +у 2 = =3х 2 (х 2 +у 2 )+ 2у 2 (х 2 +у 2 )+у 2 = 3х 2 ∙ 1+ 2у 2 ∙ 1+у 2 = 3х 2 + 3у 2 = 3(х 2 + у 2 ) = 3∙ 1=3. Ответ: 3. " width="640"

Решение олимпиадных задач

• Задача 3 ( пособие Э.Н.Балаян . «750 лучших олимпиадных и занимательных задач по математике. 7-8 классы». Ростов-на-Дону: «Феникс», 2014)
• Доказать, что разность квадратов двух нечетных чисел делится на 8.
• Решение. Составлю эту разность: А= (2n+1) 2 – (2k+1) 2 =
• =(2n+1- 2k -1)(2n+1+2k+1)=2(n - k)2(n+k+1)=4(n-k)(n+k+1)|. Если nk, то из чисел n – k и n+k+1 одно обязательно четное, значит А кратно 8.
• Задача 4 (олимпиады прошлых лет)
• Вычислить значение выражения Зх 4 +2у 4 + 5х 2 у 2 +у 2 , если х 2 +у 2 =1.
• Решение. Зх 4 +2у 4 + 5х 2 у 2 +у 2 = Зх 4 + 3х 2 у 2 +2х 2 у 2 +2у 4 +у 2 =

=3х 2 (х 2 +у 2 )+ 2у 2 (х 2 +у 2 )+у 2 = 3х 2 ∙ 1+ 2у 2 ∙ 1+у 2 = 3х 2 + 3у 2 = 3(х 2 + у 2 )

= 3∙ 1=3.

• Ответ: 3.

«Мало иметь хороший ум, главное – уметь его применять» Р.Декарт Я полностью согласен с Р. Декартом. Гипотеза подтвердилась.

Спасибо за внимание!

Список используемой литературы

• Список используемой литературы
• Учебник «Алгебра 7 класс». Под редакцией С.А.Теляковского. – М: «Просвещение», 2014
• Учебник «Алгебра 7 класс». А.Г.Мордкович – М: «Мнемозина», 2014
• Пособие «Школьные математические олимпиады. 5-11 классы» А.В.Фарков – м: «ВАКО», 2014
• Пособие Э.Н.Балаян . «750 лучших олимпиадных и занимательных задач по математике. 7-8 классы». Ростов-на-Дону: «Феникс», 2014)
• Сайт учителя математики.[Электронный ресурс] – Режим доступа: http://le-savchen.ucoz.ru/publ/1-1-0-31 свободный