Различные способы решения квадратных уравнений

«Дискриминант. Решение квадратных уравнений различными способами»

Выполнил работу Ученик 8А класса

Ковтун Артем Артемович

Руководитель проекта

Учитель математики

Силькунова Ольга Владимировна

Актуальность темы

Актуальность этой темы:  заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением  квадратных  уравнений.  Поэтому каждый ученик должен уметь верно и рационально решать  квадратные уравнения,  это также может мне  пригодится при решении более сложных задач, в том числе и при сдаче экзаменов.

Цели работы

• Цель данного индивидуального проекта состоит в рассмотрении формулировки, практического применения, а также история возникновения «Дискриминанта».
• Задачи индивидуального проекта включают в себя:
• исследовать историю открытия дискриминанта
• привести формулировки дискриминанта
• определить направления применения
• привести примеры использования дискриминанта при решении квадратных уравнений

ИСТОРИЯ ВОЗНИКНОВЕНИЯ ДИСКРИМИНАНТА

• Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись.
• Решением квадратных уравнений занимались и в Древней Греции такие ученые как Диофант, Евклид и Герон.
• Занимались решением квадратных уравнений и в Индии. Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г.
• В период Раннего Средневековья Средняя Азия становится мировым центром наук, подарившим миру многочисленных учёных. К числу знаменитых учёных того времени принадлежит аль-Хорезми Мухаммед Бен Муса. Учёный дал классификацию числовых линейных и квадратных уравнений и метод их решения.
• Формулы решения квадратных уравнений в Европе впервые были изложены в  « Книге абака »  (1202 г.) итальянским математиком Леонардо Фибоначчи. Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы.
• Лишь в XVII в., благодаря трудам Жирара, Декарта, Ньютона и других учёных, способ решения принимает современный вид. Первым, кто написал дискриминант в математическом виде, считается немецкий ученый Иога́нн Карл Фри́дрих  Гаусс. А назвал дискриминант дискриминантом британский математик Джеймс Джозеф Сильвестр в 1851.
• Таким образом, квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.

Решение квадратных уравнений различными способами

Квадратным уравнением   называют уравнение вида ах²+bх+с=0, где коэффициенты а, b, с - любые действительные числа, причем, а≠0. Коэффициенты а, b, с, различают по названиям: а – первый или старший коэффициент; b – второй или коэффициент при х; с – свободный член, свободен от переменной х.

Дискриминант

Пусть дано квадратное уравнение ах²+bх+с=0. Тогда дискриминант — это просто число D = b 2 − 4ac. Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение.

Если второй коэффициент уравнения четный, можно решать уравнение через k, тогда будет другая формула дискриминанта: D1=k 2 -ac.

ТЕОРЕМА ВИЕТА

В математике существуют специальные приемы, с которыми многие квадратные уравнения решаются очень быстро и без дискриминантов. Более того, при надлежащей тренировке многие начинают решать квадратные уравнения устно, буквально «с первого взгляда». Мы рассмотрим один из таких приемов — теорему Виета.

Теорема звучит так: сумма корней приведённого квадратного уравнения x 2  + bx + c = 0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену .

Значимость теоремы Виета заключается в том, что, не зная корней квадратного трехчлена, мы легко можем вычислить их сумму и произведение, то есть простейшие симметричные многочлены от двух переменных  x1+x2 и  x1 x2  . Теорема Виета позволяет угадывать целые корни квадратного трехчлена.

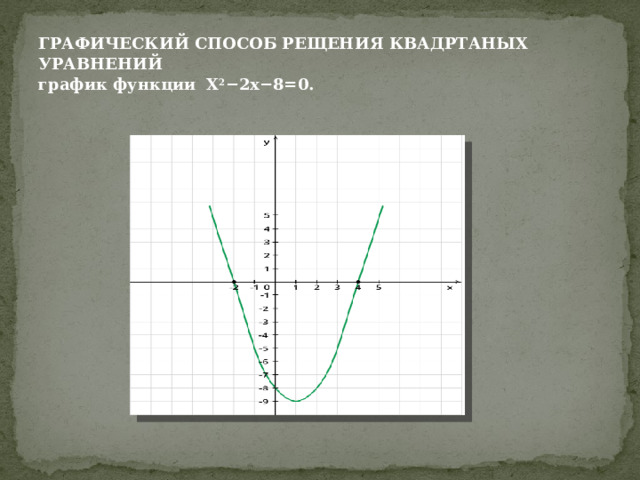
ГРАФИЧЕСКИЙ СПОСОБ РЕЩЕНИЯ КВАДРТАНЫХ УРАВНЕНИЙ график функции  Х 2 −2x−8=0 .

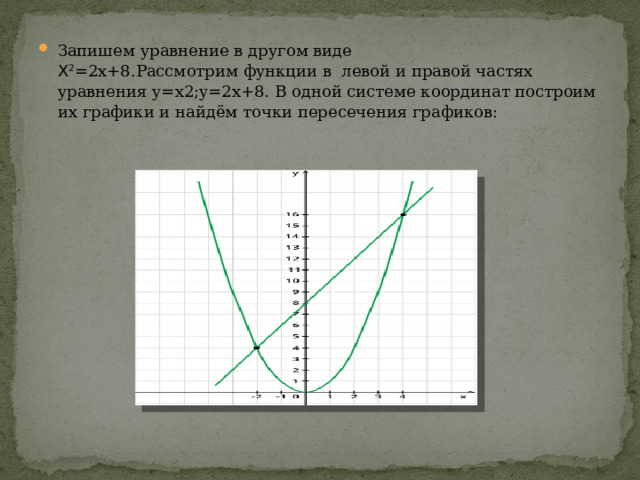
• Запишем уравнение в другом виде  Х 2 =2x+8.Рассмотрим функции в  левой и правой частях уравнения y=x2;y=2x+8. В одной системе координат построим их графики и найдём точки пересечения графиков:

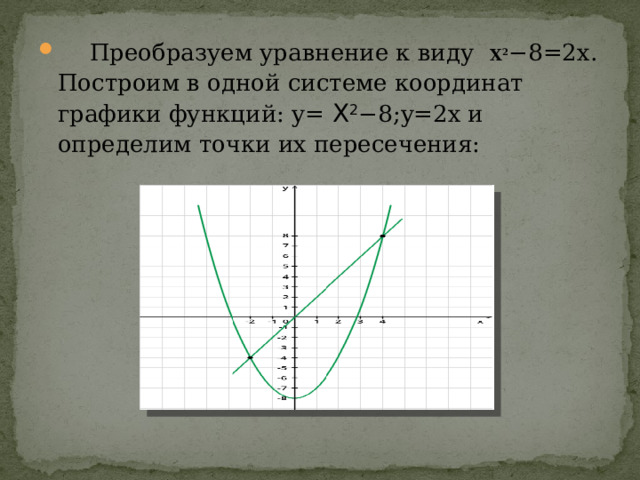
• Преобразуем уравнение к виду  Х 2 −8=2x. Построим в одной системе координат графики функций: y= Х 2 −8;y=2x и определим точки их пересечения:

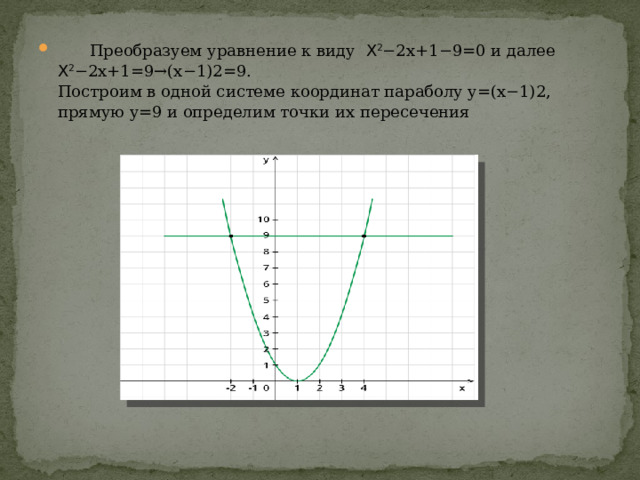
• Преобразуем уравнение к виду  Х 2 −2x+1−9=0 и далее  Х 2 −2x+1=9→(x−1)2=9. Построим в одной системе координат параболу y=(x−1)2, прямую y=9 и определим точки их пересечения

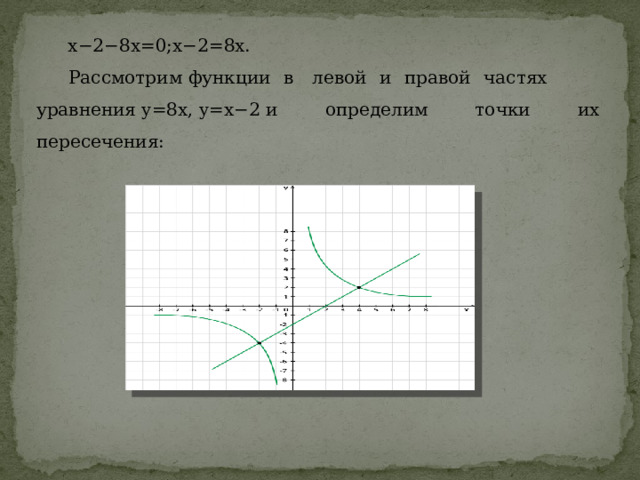
x−2−8x=0;x−2=8x.

Рассмотрим функции в  левой и правой частях уравнения y=8x, y=x−2 и определим точки их пересечения:

Решения квадратных уравнений по свойствам коэффициента

Дано квадратное уравнение ax 2  + bx + c = 0.   Если          a + b + c = 0 (сумма коэффициентов), то

x 1  = 1, x 2  = c/a

х 2  + х – 2 = 0;

Свойство 2

Дано квадратное уравнение  ax 2  + bx + c = 0.  Если           a - b + c = 0  (сумма коэффициентов), когда b взято с противоположным знаком или a + c = b, то 

x 1  = -1, x 2  = -c/a

Свойство 3

Если в квадратном уравнении  ax 2  + bx + c = 0.  Коэффициент b представлен в виде 2k, т.е. является четным числом, то формулу корней уравнения можно переписать в более простом виде

D = (b/2)2 + a*c

Заключение

Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в математике. Эти знания могут пригодиться нам на протяжении всей жизни, а так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должны заинтересовать увлекающихся математикой.

Спасибо за внимание.