Россия, Черногорск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 21.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 25.05.2025 15:36
Быкова Светлана Таировна
учитель математики и физики
48 лет
71
226 835 
Местоположение
Специализация
Различные способы решения задач на концентрацию
Категория:
Математика
29.09.2024 23:50
Просмотр содержимого документа
«Различные способы решения задач на концентрацию»
Различные способы решения задач на
концентрацию
Автор:
Быкова Светлана Таировна
Учитель математики и физики
МБОУ «Лицей имени А.Г. Баженова»
Ч тобы лучше понимать условия задач, необходимо знать следующие понятия:
- Чтобы лучше понимать условия задач, необходимо знать следующие понятия:
- Все получающиеся сплавы или смеси однородны.
- При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
- Процент - одна сотая любого вещества.
- Концентрацией вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе. (Это отношение может быть выражено либо в дробях, либо в процентах).
- Сумма концентраций всех компонент, составляющих смесь, равна единице.
типы задач
- на вычисление концентрации;
- на вычисление количества чистого вещества в смеси (или сплаве);
- на вычисление массы смеси (сплава).
Способы решения задач
- с помощью таблиц;
- с помощью схемы;
- по правилу креста;
- старинным арифметическим способом;
- алгебраическим способом;
- с помощью графика;
- с помощью формулы.
Рассмотрим несколько задач и решим их различными способами.
Задача 1 . Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?
- Решение: 1 способ – с помощью таблицы:
Наименование веществ, смесей
Наименование веществ, смесей
Исходный раствор
70 % = 0,7
Масса
раствора (г)
Воды долили
Новый раствор
Масса вещества (г)
200
-
8 % = 0,08
0,7·200
x
-
200 + x
0,08(200 + x )
Так как подливали только воду, масса уксусной кислоты в растворе не изменилась. Составляем уравнение :
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ :1,55 кг воды.
2 способ - с помощью схемы: Пусть в сосуд долили х литров воды. Получаем схему:
Уксусная Уксусная
кислота кислота
70% + х литров 8%
воды
200 г. (200 + х) г.
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ :1,55 кг воды.
.
Задача 3: Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение: 1 способ – с помощью формулы.
Пусть количество каждого из растворов было V .
Тогда количество сухого вещества в первом растворе 0,15 V , а во втором – 0,19 V . После того как растворы смешали их общий объем стал 2 V , а количество сухого вещества в смеси стало 0,15 V +0,19 V . Концентрация раствора равна:
Таким образом, концентрация полученного раствора равна:
Ответ: 17.
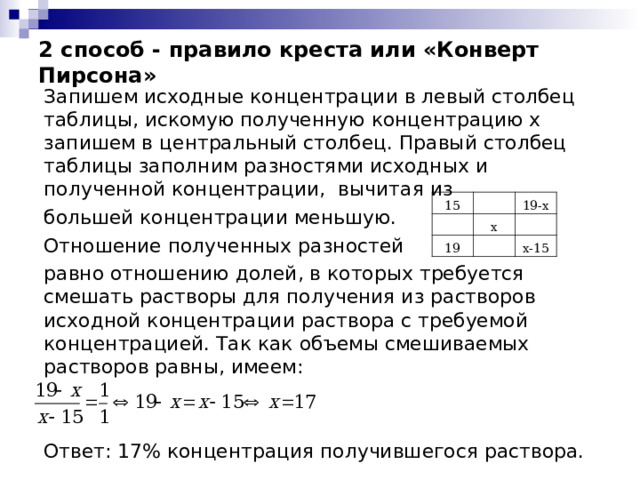
2 способ - правило креста или «Конверт Пирсона»
Запишем исходные концентрации в левый столбец таблицы, искомую полученную концентрацию х запишем в центральный столбец. Правый столбец таблицы заполним разностями исходных и полученной концентрации, вычитая из
большей концентрации меньшую.
Отношение полученных разностей
равно отношению долей, в которых требуется смешать растворы для получения из растворов исходной концентрации раствора с требуемой концентрацией. Так как объемы смешиваемых растворов равны, имеем:
Ответ: 17% концентрация получившегося раствора.
15
19-х
х
19
х-15
2 способ - алгебраический.
Пусть первого сплава было x грамм, а второго y грамм. Тогда их масса равна x+y=200, а концентрация равна 0,15x+0,65y=0,3*200. Получаем систему уравнений:
Ответ :надо взять140г. первого сплава и 60г. второго сплава.
3 способ – старинный способ решения «метод рыбки .
Узнаем сколько грамм сплава приходится на 1 часть:
200: (35+15) = 4 (грамма ) – в 1 части
15*4=60 (грамм) – 2 сплав
35*4=140 (грамм) – 1 сплав
Ответ : надо взять140г. первого сплава и 60г. второго сплава
Задача 7: Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора. На сколько граммов масса первого раствора меньше массы второго?
Решение: 1 способ – алгебраический.
Обозначим x массу первого раствора,
тогда масса второго (600 - x).
Составим уравнение:
0,3x + 0,1* (600 - x) = 600 * 0,15,
0,3х + 60 - 0,1х = 90,
0,2х = 30,
x = 150.
600 - 150 = 450 г; 450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора
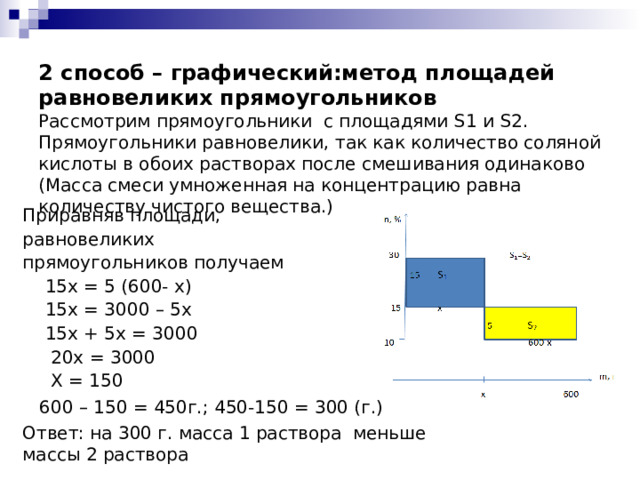
2 способ – графический:метод площадей равновеликих прямоугольников Рассмотрим прямоугольники с площадями S 1 и S 2. Прямоугольники равновелики, так как количество соляной кислоты в обоих растворах после смешивания одинаково (Масса смеси умноженная на концентрацию равна количеству чистого вещества.)
Приравняв площади,
равновеликих
прямоугольников получаем
15x = 5 (600- x)
15х = 3000 – 5х
15х + 5х = 3000
20х = 3000
Х = 150
600 – 150 = 450г.; 450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора
Заключение.
В ходе рассмотрения способов решения задач на концентрацию мы увидели красоту, сложность и притягательность данных способов.
Выбор способа решения зависит от конкретной задачи и от умения решающего.
Спасибо за внимание!
© 2024, Быкова Светлана Таировна 205 1
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
