Тема урока: «Разложение квадратного трёхчлена на множители» (урок № 1)
Предмет алгебра класс 9.
Тип урока: изучения и первичного закрепления новых знаний.
Цель урока: создать содержательные и организационные условия для восприятия, осмысления и первичного закрепления учащимися правила разложения квадратного трёхчлена на множители.
Задачи:
- обучающие: научить учащихся раскладывать на множители квадратный трёхчлен, научить применять алгоритм разложения на множители квадратного трехчлена при решении примеров, рассмотреть задания базы данных ГИА, в которых используется алгоритм разложения квадратного трёхчлена на множители
-развивающие: развивать у школьников умение формулировать проблемы, предлагать пути их решения, содействовать развитию у школьников умений выделять главное в познавательном объекте.
-воспитательные: помочь учащимся осознать ценность совместной деятельности, содействовать развитию у детей умений осуществлять самоконтроль, самооценку и самокоррекцию учебной деятельности.
Формы работы учащихся: фронтальная работа, работа в парах, индивидуальные задания, групповая работа.
Структура и ход урока
1.Организационный момент:
2. Актуализация знаний:
Самостоятельная работа ( классу раздать листочки с текстом самостоятельной работы) (Приложение 1)
Самостоятельная работа
Разложите на множители:
x 2 – 3x;
x 2 – 9;
x 2 – 8x + 16;
2a 2 – 2b 2 –a + b;
2x 2 – 7x – 4.
Сократить дробь:
 ,
,

Вопрос классу:
- Какие способы разложения многочлена на множители вы использовали?
- Все ли многочлены вы смогли разложить на множители?
-Все ли дроби смогли сократить?
Проблема2:
- Как разложить на множители многочлен
2x 2 – 7x – 4?
-Как сократить дробь  ?
?
Фронтальный опрос:
- Что собой представляют многочлены
2x 2 – 7x – 4 и x 2 – 5x +6?
-Дайте определение квадратного трёхчлена.
- Что мы знаем о квадратном трёхчлене?
- Как найти его корни?
- От чего зависит количество корней?
- Сопоставьте эти знания с тем, что мы должны узнать и сформулируйте тему урока. ( После этого на экране тема урока)
- Поставим цель урока
- Наметим конечный результат
3. Изучение нового учебного материала.
Вопрос классу: Как решить эту проблему?
Класс работает в группах.
Задание группам:
по оглавлению найти нужную страницу, с карандашом в руках прочитать п.4 , выделить главную мысль, составить алгоритм, по которому любой квадратный трёхчлен можно разложить на множители.
Проверка выполнения задания классом (фронтальная работа):
-Какова главная мысль пункта 4? (на экране формула разложения квадратного трёхчлена на множители ).
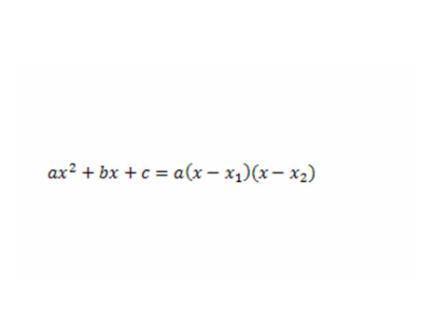
Алгоритм на экране.
1.Приравнять квадратный трёхчлен к нулю.
2.Найти дискриминант.
3.Найти корни квадратного трёхчлена.
4.Подставить найденные корни в формулу.
5.Если необходимо, то внести старший коэффициент в скобки.
-Ещё одна маленькая проблема: если D=0, то можно ли разложить квадратный трёхчлен на множители, и если можно, то как?
Если D = 0, то 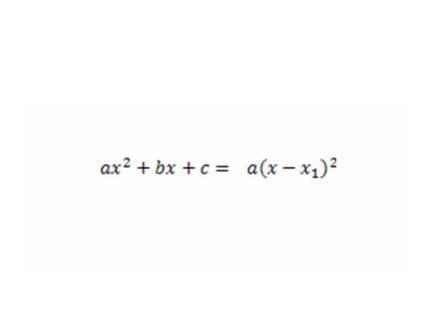 .
.
Если квадратный трехчлен не имеет корней,
то его разложить на множители нельзя.)
-Вернёмся к заданию в самостоятельной работе. Сможем ли теперь разложить на множители квадратные трёхчлены 2x 2 – 7x – 4 и x 2 – 5x +6?
Класс работает самостоятельно, раскладывает на множители, я работаю индивидуально со слабыми учащимися.
4. Закрепление изученного материала
Сможем ли сократить дробь  ?
?
Сократить дробь, вызываю к доске сильного ученика.
Вернёмся к заданию из ГИА. Сможем ли мы теперь построить график функции ?
?
Что является графиком данной функции?
Постройте график функции у себя в тетради.
Тест (самостоятельная работа) Приложение 2
Самопроверка и самооценка Учащимся выданы листочки (Приложение 3), в которые надо записать ответы. В них даны критерии оценок.
Критерии оценок:
Верно выполнено: 2 задание – оценка«3»
3 задания – оценка»4»
4задания – оценка «5»
5. Итог урока





 ,
,










