Размещение сайта в интернете

ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ

Ключевые слова

• алгебра логики
• высказывание
• логическая операция
• конъюнкция
• дизъюнкция
• отрицание
• логическое выражение
• таблица истинности
• законы логики

Л огик а

Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение).

Джордж Буль (1815-1864). Создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний).

Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике

Алгебра

Алгебра - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами – числами, многочленами, векторами и др.

Высказывание

Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное .

В русском языке высказывания выражаются повествовательными предложениями:

Земля вращается вокруг Солнца .

Москва - столица.

Но не всякое повествовательное предложение является высказыванием:

Это высказывание ложное.

Побудительные и вопросительные предложения высказываниями не являются.

Без стука не входить!

Откройте учебники.

Ты выучил стихотворение?

Высказывание или нет?

Зимой идет дождь.

Снегири живут в Крыму.

Кто к нам пришел?

У треугольника 5 сторон.

Как пройти в библиотеку?

Переведите число в десятичную систему.

Запишите домашнее задание

• Зимой идет дождь. Снегири живут в Крыму. Кто к нам пришел? У треугольника 5 сторон. Как пройти в библиотеку? Переведите число в десятичную систему. Запишите домашнее задание

Алгебра логики

Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.

В алгебре логики высказывания обозначают буквами и называют логическими переменными .

Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей ( А = 1 ), а если ложно - нулём ( В = 0 ).

0 и 1 называются логическими значениями .

Простые и сложные высказывания

Высказывания бывают простые и сложные.

Высказывание называется простым , если никакая его часть сама не является высказыванием.

Сложные (составные) высказывания строятся из простых с помощью логических операций .

Название логической операции

Конъюнкция

Логическая связка

Дизъюнкция

«и»; «а»; «но»; «хотя»

«или»

Инверсия

«не»; «неверно, что»

Логические операции

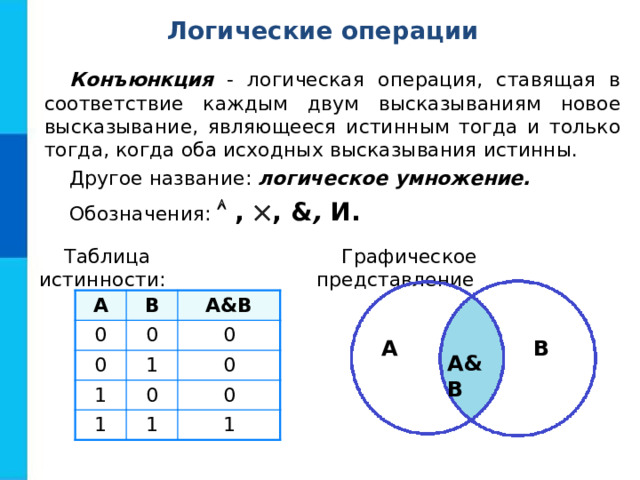
Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Другое название: логическое умножение.

Обозначения:  ,  , & , И.

Таблица истинности:

Графическое представление

А

0

В

А & В

0

0

0

1

1

1

0

0

0

1

1

A

B

А & В

Логические операции

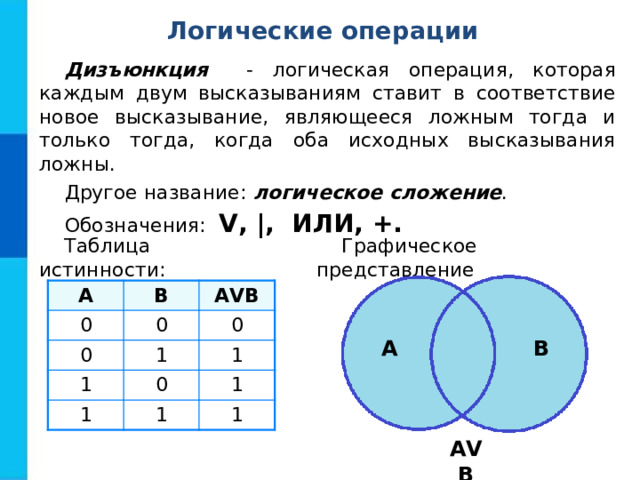
Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Другое название: логическое сложение .

Обозначения: V , |, ИЛИ, +.

Графическое представление

Таблица истинности:

А

0

В

А V В

0

0

0

1

1

1

0

1

1

1

1

A

B

А V В

Логические операции

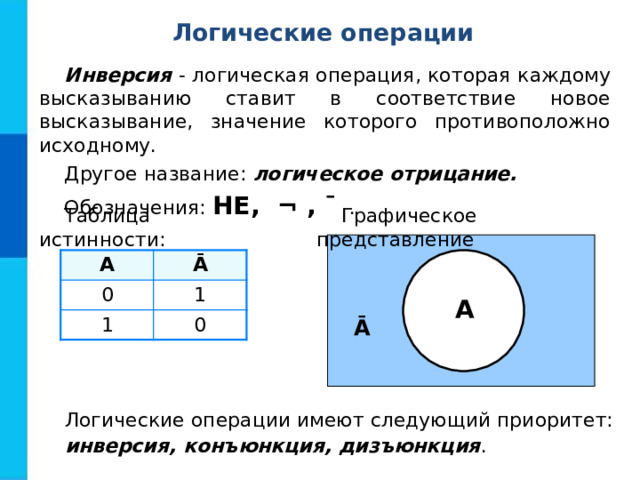
Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

Другое название: логическое отрицание.

Обозначения: НЕ, ¬ , ¯ .

Таблица истинности:

Графическое представление

А

0

Ā

1

1

0

A

Ā

Логические операции имеют следующий приоритет:

инверсия, конъюнкция, дизъюнкция .

Решаем задачу

Пусть А = «На Web-странице встречается слово "крейсер"», В = «На Web-странице встречается слово "линкор"».

В некотором сегменте сети Интернет 5000000 Web-страниц. В нём высказывание А истинно для 4800 страниц, высказывание В - для 4500 страниц, а высказывание А V В - для 7000 страниц.

Для какого количества Web-страниц в этом случае будут истинны следующие выражения и высказывание?

а) НЕ ( А ИЛИ В );

б) А & B ;

в) На Web-странице встречается слово "крейсер" И НЕ встречается слово "линкор".

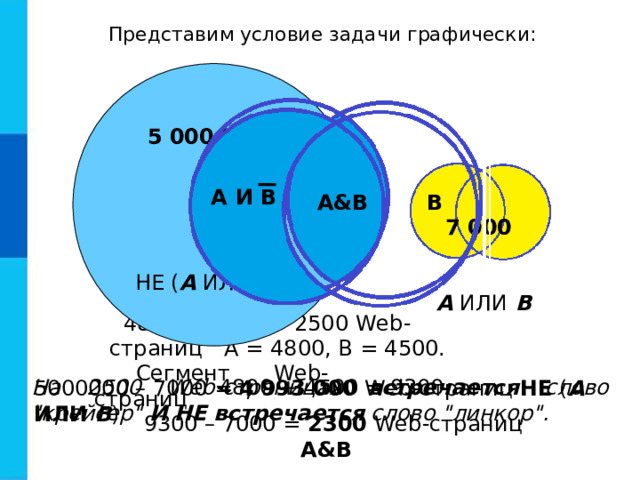
Представим условие задачи графически:

5 000 000

B

И

A

A

B

A&B

7 000

НЕ ( А ИЛИ В )

А ИЛИ В

4800 – 2300 = 2500 Web -страниц

A = 4800, B = 4500.

4800 + 4500 = 9300

Сегмент Web- страниц

На 2500 Web-страницах встречается слово "крейсер" И НЕ встречается слово "линкор".

5000000 – 7000 = 4 993 000 Web -страниц НЕ ( А ИЛИ В )

9300 – 7000 = 2300 Web -страниц A&B

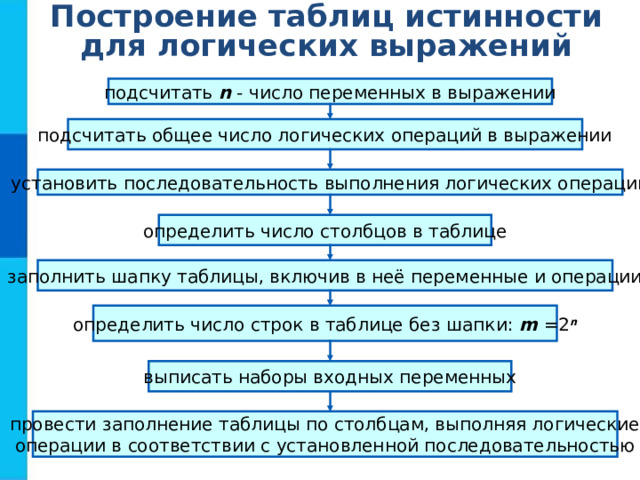
Построение таблиц истинности для логических выражений

подсчитать n - число переменных в выражении

подсчитать общее число логических операций в выражении

установить последовательность выполнения логических операций

определить число столбцов в таблице

заполнить шапку таблицы, включив в неё переменные и операции

определить число строк в таблице без шапки: m =2 n

выписать наборы входных переменных

провести заполнение таблицы по столбцам, выполняя логические

операции в соответствии с установленной последовательностью

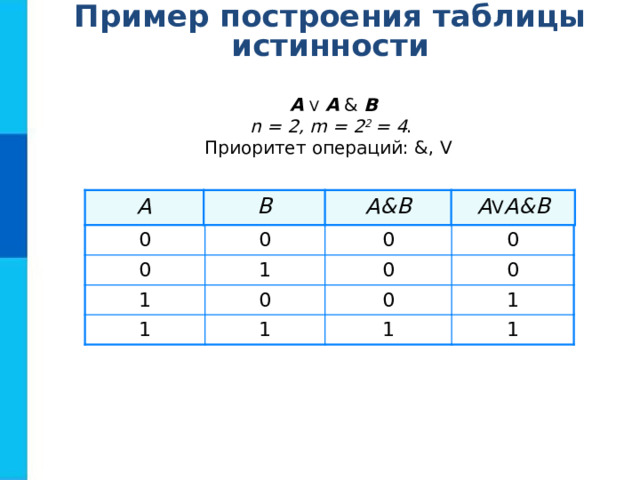
Пример построения таблицы истинности

А V A & B

n = 2, m = 2 2 = 4 .

Приоритет операций: &, V

A

B

A&B

A V A&B

0

0

0

1

0

1

0

1

0

0

0

1

0

1

1

1

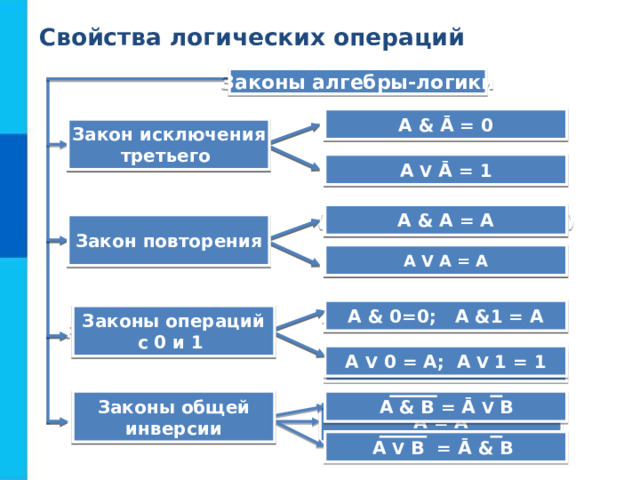
Свойства логических операций

Законы алгебры-логики

A & Ā = 0

A & B = B & A

Закон исключения

третьего

Переместительный

A V Ā = 1

A V B = B V A

A & A = A

(A & B) & C = A & ( B & C)

Закон повторения

Сочетательный

(A V B) V C =A V ( B V C)

A V A = A

A&(B V C)= (A&B) V (A&C)

A & 0=0; A &1 = A

Распределительный

Законы операций

с 0 и 1

A V 0 = A; A V 1 = 1

A V (B&C) = (A V B)&(A V C)

Закон двойного

отрицания

Законы общей

инверсии

A & B = Ā V B

Ā = A

A V B = Ā & B

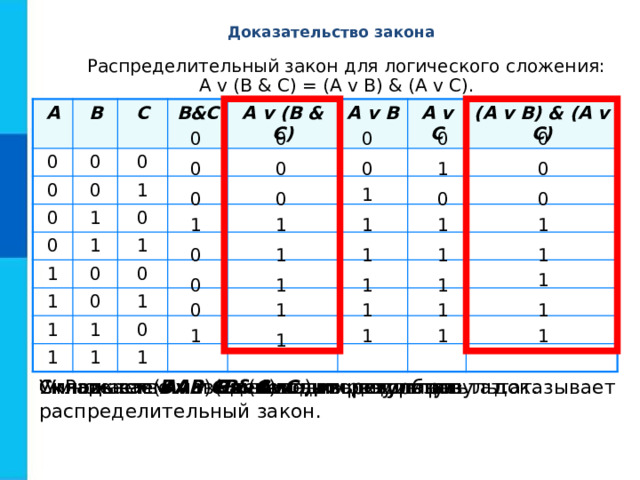
Доказательство закона

Распределительный закон для логического сложения: A v (B & C) = (A v B) & (A v C).

A

B

0

C

0

0

B&C

0

0

0

A v (B & C)

0

1

1

A v B

0

1

1

A v C

1

0

1

(A v B) & (A v C)

0

0

1

1

1

1

0

1

1

0

0

0

0

0

0

0

0

1

0

1

0

0

0

0

1

1

1

1

1

1

1

1

0

1

1

1

1

0

1

0

1

1

1

1

1

1

1

1

1

Равенство выделенных столбцов доказывает распределительный закон.

Умножаем В на С и выводим результат.

Складываем А и ( В & С ) и выводим результат.

Умножаем ( А v B ) на ( A v C ) и выводим результат.

Складываем А и C и выводим результат.

Складываем А и В и выводим результат.

Решение логических задач

Задача. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу.

На вопрос, кто разбил вазу, они дали такие ответы:

Серёжа : 1) Я не разбивал. 2) Вася не разбивал.

Вася : 3) Серёжа не разбивал. 4) Вазу разбил Коля.

Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа.

Бабушка знала, что один из её внуков (правдивый), оба раза сказал правду; второй (шутник) оба раза сказал неправду; третий (хитрец) один раз сказал правду, а другой раз - неправду. Назовите имена правдивого, шутника и хитреца.

Кто из внуков разбил вазу?

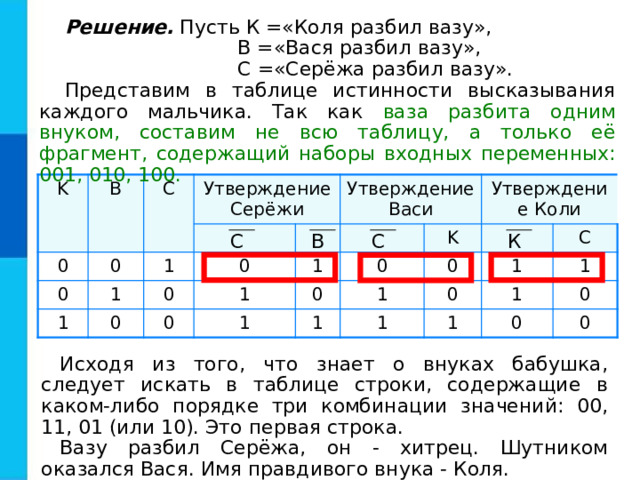
Решение. Пусть К =«Коля разбил вазу»,

В =«Вася разбил вазу»,

С =«Серёжа разбил вазу».

Представим в таблице истинности высказывания каждого мальчика. Так как ваза разбита одним внуком, составим не всю таблицу, а только её фрагмент, содержащий наборы входных переменных: 001, 010, 100.

K

B

0

C

0

Утверждение Серёжи

0

1

1

1

0

0

Утверждение Васи

0

0

1

1

Утверждение Коли

0

1

0

K

1

0

1

1

1

0

C

1

1

1

0

0

0

С

В

К

С

Исходя из того, что знает о внуках бабушка, следует искать в таблице строки, содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10). Это первая строка.

Вазу разбил Серёжа, он - хитрец. Шутником оказался Вася. Имя правдивого внука - Коля.

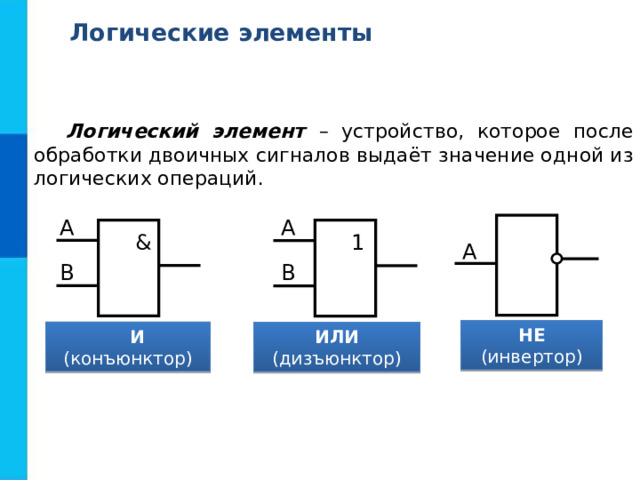
Логические элементы

Логический элемент – устройство, которое после обработки двоичных сигналов выдаёт значение одной из логических операций.

А

А

&

1

А

В

В

НЕ (инвертор)

И (конъюнктор)

ИЛИ (дизъюнктор)

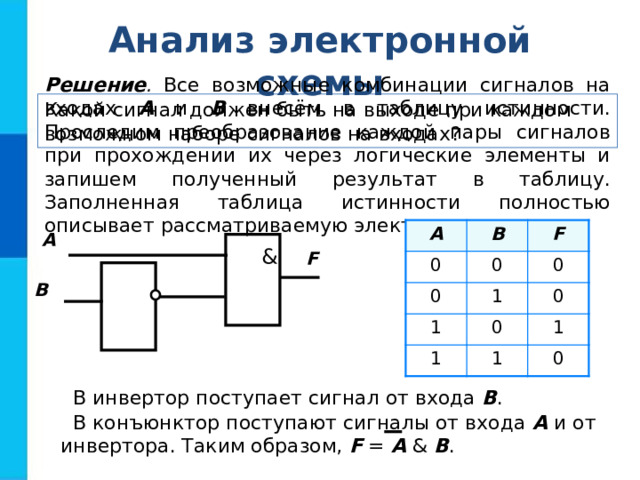
Анализ электронной схемы

Решение . Все возможные комбинации сигналов на входах А и В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную схему.

Какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах?

A

0

B

F

0

0

1

0

1

1

0

0

1

1

0

А

&

F

В

В инвертор поступает сигнал от входа В .

В конъюнктор поступают сигналы от входа А и от инвертора. Таким образом, F = A & B .

Самое главное

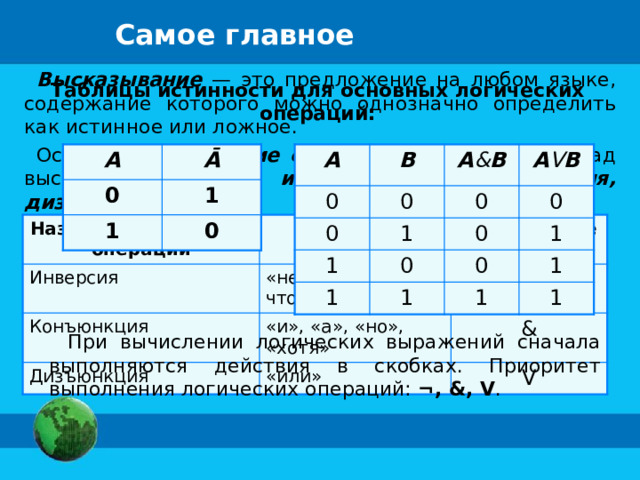
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

Основные логические операции , определённые над высказываниями: инверсия, конъюнкция, дизъюнкция .

Таблицы истинности для основных логических операций:

А

0

Ā

1

A

1

B

0

0

0

0

A & B

A V B

0

1

1

0

0

1

0

1

1

0

1

1

1

Название логической операции

Инверсия

Логическая связка

«не, «неверно, что»

Обозначение

Конъюнкция

¬ , ─

Дизъюнкция

«и», «а», «но», «хотя»

«или»

&

V

При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций: ¬, &, V .

Вопросы и задания

В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание.

1) Число 376 чётное и трёхзначное.

2) Зимой дети катаются на коньках или на лыжах.

3) Новый год мы встретим на даче или на Красной площади.

4) Неверно, что Солнце движется вокруг Земли.

5) Земля имеет форму шара, который из космоса кажется голубым.

6) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу.

Объясните, почему следующие предложения не являются высказываниями.

1) Какого цвета этот дом?

2) Число Х не превосходит единицы.

3) 4 Х +3.

4) Посмотрите в окно.

5) Пейте томатный сок!

6) Эта тема скучна.

7) Рикки Мартин - самый популярный певец.

8) Вы были в театре?

Постройте отрицания следующих высказываний.

1) Сегодня в театре идёт опера «Евгений Онегин».

2) Каждый охотник желает знать, где сидит фазан.

3) Число 1 есть простое число.

4) Натуральные числа, оканчивающиеся цифрой 0, не являются простыми числами.

5) Неверно, что число 3 не является делителем числа 198.

6) Коля решил все задания контрольной работы.

7) Во всякой школе некоторые ученики интересуются спортом.

8) Некоторые млекопитающие не живут на суше.

Выясните, какой сигнал должен быть на выходе электронной схемы при каждом возможном наборе сигналов на входах. Составьте таблицу работы схемы. Каким логическим выражением описывается схема?

Пусть А = «Ане нравятся уроки математики», а В = «Ане нравятся уроки химии». Выразите следующие формулы на обычном языке:

Приведите по одному примеру истинных и ложных высказываний из биологии, географии, информатики, истории, математики, литературы.

А

1

F

В

Вопросы и задания

Алёша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:

1) Алеша : « Это сосуд греческий и изготовлен в V веке ».

2) Боря : « Это сосуд финикийский и изготовлен в III веке ».

3) Гриша : « Это сосуд не греческий и изготовлен в IV веке ».

Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?

Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и утаил клад. На следствии каждый из подозреваемых сделал два заявления:

Смит : «Я не делал этого. Браун сделал это».

Джон : «Браун не виновен. Смит сделал это».

Браун : «Я не делал этого. Джон не делал этого».

Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду.

Кто из подозреваемых должен быть оправдан?

Опорный конспект

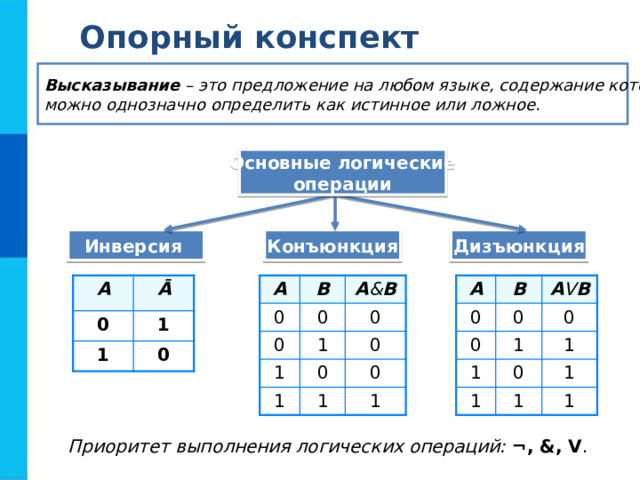
Высказывание – это предложение на любом языке, содержание которого

можно однозначно определить как истинное или ложное.

Основные логические

операции

Дизъюнкция

Конъюнкция

Инверсия

А

A

0

A

Ā

0

0

1

B

1

B

A & B

0

0

0

0

0

A V B

1

0

1

0

1

1

1

1

0

0

1

0

1

0

1

1

1

1

Приоритет выполнения логических операций: ¬, &, V .

Электронные образовательные ресурсы

• http://school-collection.edu.ru/catalog/res/9e997f40-f285-4369-aa7d-88b892beca45/?interface=catalog&class=51&subject=19 – Элементарные логические операции