Разные задачи на дроби и проценты
Задача 1. Нахождение целого по его части.
В сборнике фантастики две повести. Первая занимает 35 страниц, а вторая – 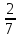 книги. Сколько всего страниц в книге?
книги. Сколько всего страниц в книге?
Решение:
Сначала найдем, какую часть рукописи занимает первая повесть: 1 – 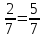 , а потом целое по его части: 35 :
, а потом целое по его части: 35 : 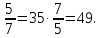
Ответ: 49 страниц.
Задача 2. Нахождение целого по его процентам.
Летом на дачу с детским садом выехали 180 детей. Известно, что 10% детей не поехали на дачу. Сколько всего детей в детском саду?
Решение:
Выразим в процентах число детей, которые поехали на дачу:
100% - 10% = 90% и продолжим решение.
Способ 1.
Составим пропорцию:
180 детей – 90%
х детей – 100%
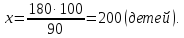
Способ 2.
Если 90% - это 180 детей, то 10% в 9 раз меньше, т.е. 20 детей, а 100% - это 200 детей.
Способ 3.
180 детей составляют 90%, т.е. 0,9 всех детей. Найдем целое по его части:
180 : 0,9 = 1800 : 9 = 200.
Ответ: 200 детей.
Задача 3. Выражение остатка через часть целого.
На пошив детской одежды ушел весь рулон ткани. Из 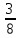 рулона сшили куртки, из четверти рулона – юбки, из оставшихся 24 м сшили несколько брюк. Сколько всего метров ткани было в рулоне?
рулона сшили куртки, из четверти рулона – юбки, из оставшихся 24 м сшили несколько брюк. Сколько всего метров ткани было в рулоне?
Решение:
Найдем, из какой части всего рулона сшили куртки и юбки: 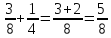 . Теперь понятно, что на пошив брюк осталась часть, равная 1 –
. Теперь понятно, что на пошив брюк осталась часть, равная 1 – 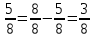 рулона, которая составляет 24 м. Значит, во всем рулоне было 24 :
рулона, которая составляет 24 м. Значит, во всем рулоне было 24 : 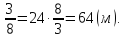
Ответ: 64 м.
Задача 4. Выражение остатка процентами целого.
Андрей за работу над новым проектом получил премию. Он истратил часть денег на подарки: 5% - родителям, 10% - жене, 7% - сыну и у него осталось
11700 р. Какую сумму денег составила премия?
Решение:
Выразим в процентах количество денег, оставшихся от премии:
100% - (5% + 10% + 7%) = 100% - 22% = 78%.
Способ 1.
Составим пропорцию:
11700 р. – 78%
х рублей – 100%
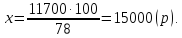
Способ 2.
78 % выражаются дробью 0,78. Вычислим целое по его проценту:
11700 : 0,78 = 1170000 : 78 = 15000(р)
Ответ: 15000 рублей.
Задача 5. Выражение величины частью целого.
Оля истратила треть имевшейся у нее суммы денег, а потом еще 100 р. В итоге она истратила половину суммы. Сколько денег было у Оли первоначально?
Решение:
Сначала узнаем, какую часть всей суммы составляет 100 р.:
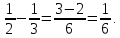
Теперь мы знаем, что 100 р. – это 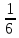 всей суммы. Чтобы ответить на вопрос задачи, нужно найти целое по его части, т.е. 100 разделить на
всей суммы. Чтобы ответить на вопрос задачи, нужно найти целое по его части, т.е. 100 разделить на 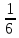 . В данном случае можно попросту 100 р. умножить на 6. Получим, что у Оли было 600 р.
. В данном случае можно попросту 100 р. умножить на 6. Получим, что у Оли было 600 р.
Ответ: 600 р.
Задача 6. Выражение величины процентами целого.
Среди участников кросса 35% студенты, остальные – старшеклассники, причем их на 252 человека больше, чем студентов. Сколько спортсменов участвует в кроссе?
Решение:
Старшеклассники составляют 100% - 35% = 65% участников кросса. Найдем, на сколько процентов больше старшеклассников, чем студентов: 65% - 35% = 30%. Эти 30% составляют 252 человека.
Способ 1.
Составим пропорцию:
252 человека – 30%
х человек – 100%
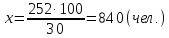
Способ 2.
30% выражаются десятичной дробью 0,3. Вычислим целое по его проценту: 252 : 0,3 = 2520 : 3 = 840 (чел.).
Ответ: 840 человек.
Задача 7. Часть от части целого.
Перед поездкой бак автомобиля был заполнен на 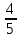 . Во время поездки была истрачена четверть имевшегося запаса бензина. Какая часть бака заполнена бензином к концу поездки?
. Во время поездки была истрачена четверть имевшегося запаса бензина. Какая часть бака заполнена бензином к концу поездки?
Решение:
По условию истрачена четверть от 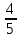 бака, значит, осталось
бака, значит, осталось 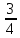 от
от 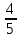 бака:
бака:
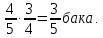
Ответ: 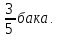
Задача 8. Проценты от процентов целого.
Четверть тиража новой газеты раскуплена в первый же день ее выпуска, причем 64% этой газеты продано в газетных киосках. Сколько процентов всего тиража продано в газетных киосках?
Решение:
Четверть тиража новой газеты составляют его 25%. Найдем 64% от 25%:
0,25 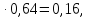 т.е. 16%.
т.е. 16%.
Ответ: 16% тиража.
Задача 9. Оставшаяся часть целого.
Ученик закрасил 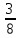 круга синим цветов и
круга синим цветов и 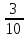 оставшейся части – желтым цветом. Какая часть круга осталась незакрашенной?
оставшейся части – желтым цветом. Какая часть круга осталась незакрашенной?
Решение:
Способ 1.
После закрашивания синим цветом остались незакрашенными 1 – 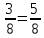 круга. Найдем
круга. Найдем 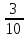 от
от 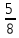 :
:  Сложим закрашенные части:
Сложим закрашенные части:  Значит, незакрашенными остались: 1
Значит, незакрашенными остались: 1 
Способ 2.
После закрашивания синим цветом остались незакрашенными 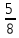 круга. После закрашивания желтым цветом остались незакрашенными 1 –
круга. После закрашивания желтым цветом остались незакрашенными 1 –  оставшейся части. Найдем
оставшейся части. Найдем  от
от 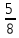 :
:  .
.
Ответ:  круга.
круга.
Задача 10. Оставшиеся проценты целого.
Автомобиль прошел 40% пути, а затем 30% оставшегося расстояния. Сколько процентов всего пути ему осталось пройти?
Решение:
Способ 1.
После того как автомобиль прошел 40% пути, ему осталось еще пройти:
100% – 40% = 60% пути. Найдем 30%, т.е. 0,3 от 60%: 60 %. Значит, всего автомобиль прошел 40% + 18% = 58% пути и ему осталось пройти
%. Значит, всего автомобиль прошел 40% + 18% = 58% пути и ему осталось пройти
100% – 58%=42% пути.
Способ 2.
После того как автомобиль прошел 40% пути, ему осталось еще пройти 60% пути. А когда он пройдет 30% оставшегося расстояния, то ему останется пройти 70% оставшегося расстояния. Найдем 70%, т.е. 0,7 от 60:
60  %.
%.
Ответ: 42%.
Задача 11. Сложение процентов.
В школе 16% девочек и 28% мальчиков занимаются в спортивных секциях. Сколько всего процентов школьников занимаются в спортивных секциях, если число мальчиков и число девочек в школе одинаково?
Решение:
Число мальчиков и девочек в школе одинаково, а значит, в школе 50% мальчиков и 50% девочек. Найдем 16%, т.е. 0,16 от 50%: 50  %. Найдем 28%, т.е. 0,28 от 50%: 50
%. Найдем 28%, т.е. 0,28 от 50%: 50  %. Сложим проценты: 8% + 14% = 22% - столько процентов составляют учащиеся школы, которые занимаются в спортивных секциях.
%. Сложим проценты: 8% + 14% = 22% - столько процентов составляют учащиеся школы, которые занимаются в спортивных секциях.
Ответ: 22% школьников.
Задача 12. Уменьшение (увеличение) на несколько процентов.
На весенней распродаже в одном магазине товар уценили на 40%, а через неделю еще на 5%. На ярмарке тот же товар уценили сразу на 45%. Где выгоднее покупателю купить эту вещь?
Решение:
Товар выгоднее купить там, где он дешевле. В магазине после двух уценок цена товара составит 0,6  его первоначальной цены, а на ярмарке – 0,55 первоначальной цены. Так как 0,57 0,55, то правильный ответ: на ярмарке.
его первоначальной цены, а на ярмарке – 0,55 первоначальной цены. Так как 0,57 0,55, то правильный ответ: на ярмарке.
Ответ: на ярмарке.
Задача 13. Сравнение величин.
Во время распродажи кресло, стоившее 3000 р., продавали за 2400 р. На сколько процентов была снижена цена кресла на распродаже?
Решение:
Способ 1.
На сколько рублей новая цена меньше старой? На 3000 – 2400 = 600 рублей. На какую часть была снижена цена кресла? На  , что составляет 20%
, что составляет 20%
Способ 2.
Какую часть новая цена составляет от старой?  , т.е. 80%. А это значит, что цена снижена на 100% – 80% = 20%.
, т.е. 80%. А это значит, что цена снижена на 100% – 80% = 20%.
Способ 3.
Составим пропорцию:
3000 р. – 100%
2400 р. – х%

100% – 80% = 20%.
Ответ: цена снижена на 20%.
Задача 14. Отношение процентов.
Отношение числа девочек в школе к числу мальчиков равно 4 : 5. Какую часть составляют девочки от числа всех учащихся школы? А мальчики? Выразите ответ в процентах.
Решение:
Если отношение числа девочек в школе к числу мальчиков равно 4 : 5, то число девочек составляет 4 части, а мальчиков 5 частей, а число всех учащихся школы – 9 таких же частей. Поэтому девочки от числа всех учащихся школы составляют  , а мальчики
, а мальчики  .
.
Ответ: примерно 44% и 56%.
Задача 15. «Потери», выраженные в процентах.
При сушке яблоки теряют 75% своей массы, т.е. ту часть влаги, которая из нее выпаривается. Сушеные яблоки содержат 20% влаги. Какова влажность свежих яблок?
Решение:
Масса сушеных яблок составляет 100% – 75% = 25% массы свежих яблок, и она содержит 0,25  т.е. 5% влаги. Таким образом, влажность свежих яблок 75% + 5% = 80%.
т.е. 5% влаги. Таким образом, влажность свежих яблок 75% + 5% = 80%.
Ответ: 80% массы.
Задача 16. Концентрация раствора.
Сколько граммов воды надо добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, содержащий 20% сахара?
Решение:
Способ 1.
Определим, сколько сахара в данной массе сиропа: 180  Теперь найдем, сколько граммов 20-процентного сиропа получится, если взять 45 г сахара: 45 : 0,2 = 225 (г). Таким образом, в данную массу сиропа надо добавить
Теперь найдем, сколько граммов 20-процентного сиропа получится, если взять 45 г сахара: 45 : 0,2 = 225 (г). Таким образом, в данную массу сиропа надо добавить
225 – 180 = 45 (г) воды.
Способ 2.
Решим задачу методом «стаканчиков».
25% 0% 20%



+ =
180 г х г (180 + х) г
Составим уравнение:
4500 = 3600 + 20х
20х = 900

х = 45
Ответ: 45 г.







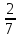 книги. Сколько всего страниц в книге?
книги. Сколько всего страниц в книге?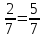 , а потом целое по его части: 35 :
, а потом целое по его части: 35 : 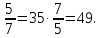
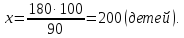
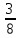 рулона сшили куртки, из четверти рулона – юбки, из оставшихся 24 м сшили несколько брюк. Сколько всего метров ткани было в рулоне?
рулона сшили куртки, из четверти рулона – юбки, из оставшихся 24 м сшили несколько брюк. Сколько всего метров ткани было в рулоне?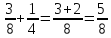 . Теперь понятно, что на пошив брюк осталась часть, равная 1 –
. Теперь понятно, что на пошив брюк осталась часть, равная 1 – 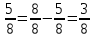 рулона, которая составляет 24 м. Значит, во всем рулоне было 24 :
рулона, которая составляет 24 м. Значит, во всем рулоне было 24 : 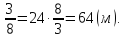
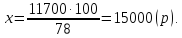
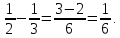
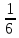 всей суммы. Чтобы ответить на вопрос задачи, нужно найти целое по его части, т.е. 100 разделить на
всей суммы. Чтобы ответить на вопрос задачи, нужно найти целое по его части, т.е. 100 разделить на 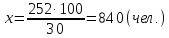
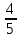 . Во время поездки была истрачена четверть имевшегося запаса бензина. Какая часть бака заполнена бензином к концу поездки?
. Во время поездки была истрачена четверть имевшегося запаса бензина. Какая часть бака заполнена бензином к концу поездки?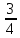 от
от 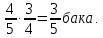
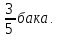
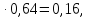 т.е. 16%.
т.е. 16%.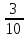 оставшейся части – желтым цветом. Какая часть круга осталась незакрашенной?
оставшейся части – желтым цветом. Какая часть круга осталась незакрашенной?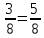 круга. Найдем
круга. Найдем 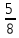 :
: 








Наглядная геометрия 5-6 классы ФГОС
Электронная тетрадь по геометрии 7...
Геометрия 7 класс
Алгебра 7 класс
Математика 6 класс
Электронная тетрадь по алгебре 10 класс...
Электронная тетрадь по алгебре 7 класс...
Математика и игры в средней школе
© 2019, Коптева Лайсан Мунавировна 19439 705
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы