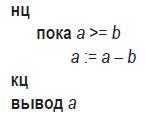Алгоритмы и программы
План
Понятие и свойства алгоритмов.
Принципы построения алгоритмов, данные о базовых конструкциях.
Понятие программы. Программирование и его виды
Понятие и свойства алгоритмов
Алгоритм — строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.
Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.
Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.

В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
Словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
Блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
Формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
Псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.
Пример 1. Записать в словесной форме правило деления обыкновенных дробей.
Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.
Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).
Формальные исполнители алгоритма
Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.
Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).
Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.
Пример 2. Исполнитель Крот имеет следующую систему команд:
вперед k — продвижение на указанное число шагов вперед;
поворот s — поворот на s градусов по часовой стрелке;
повторить m [команда1 … командаN] — повторить m раз серию указанных команд.
Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?
Повторить 5 [вперед 10 поворот 72]
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.
Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).
Пример 3. В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).
Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).
Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]
Блок–схема
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
Основные элементы блок–схемы алгоритма:

Общий вид блок–схемы алгоритма:
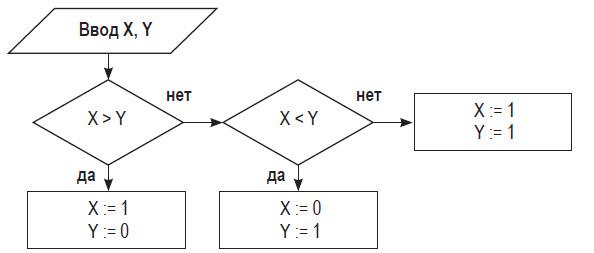
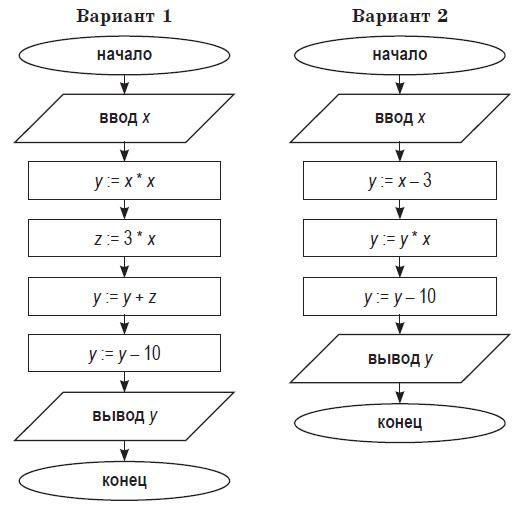
Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
Решение.
Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7
Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
Вычисляется результат выполнения алгоритма: X := 0, Y := 1.
Ответ: X := 0, Y := 1.
Алгоритмические языки
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.
В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.
Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.
Псевдокод
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.
Служебные слова учебного алгоритмического языка:
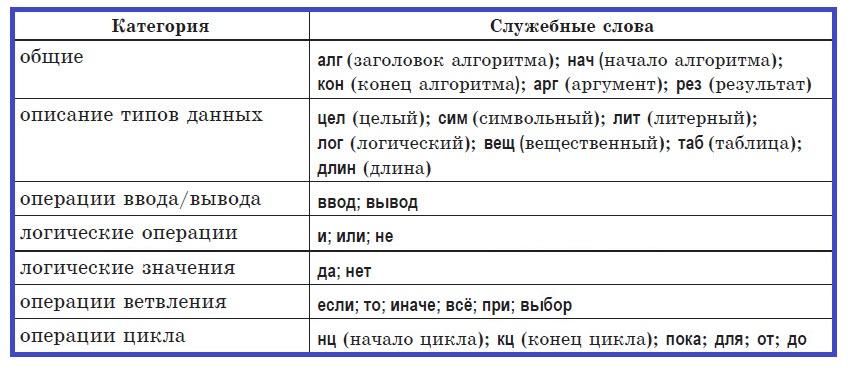
Стандартная структура алгоритма
Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.
Общий вид записи алгоритма на учебном алгоритмическом языке:

В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.
В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.
Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.
Примеры заголовков алгоритмов:

В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.
Пример алгоритма вычисления гипотенузы прямоугольного треугольника:

На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.
Принципы построения алгоритмов, данные о базовых конструкциях.
Различают три основных вида алгоритмов (базовые алгоритмические конструкции, или структуры): линейные, с разветвлениями и с циклами.
В самом простом случае алгоритм предписывает поочередное выполнение всех заданных действий независимо от значений входных данных. Например, чтобы умножить две обыкновенные дроби, необходимо перемножить отдельно их числители и знаменатели и записать их соответственно в числитель и знаменатель результата. Такие действия необходимо выполнять для умножения любых двух обыкновенных дробей.
Алгоритм, предписывающий одноразовое выполнение одной и той же последовательности действий при любых допустимых входных данных, называется линейным (линейной структурой). Использование этой структуры возможно только для простых задач.
Для решения более сложных задач могут потребоваться алгоритмы, предусматривающие два возможных варианта действий. Выбор варианта зависит от некоторого условия. В таких случаях (когда алгоритм реализует выбор одного из альтернативных путей в зависимости от результатов проверки некоторого условия) говорят о ветвлении алгоритма. Например, для решения квадратного уравнения необходимо сначала найти значение дискриминанта, а затем, в зависимости от его знака, либо сообщить об отсутствии действительных корней (если дискриминант отрицательный), либо найти их по соответствующим формулам.
Алгоритм, предписывающий выполнение тех или других действий в зависимости от результата проверки условия, называется разветвленным (структурой ветвления).
Хотя алгоритм ветвления содержит описание действий для обоих возможных вариантов, но при каждом его выполнении реализуется только один из них, какой именно — зависит от заданного набора входных данных. Следовательно, в отличие от линейного алгоритма, при реализации алгоритма с разветвлением будут выполнены не все действия, а только те, что выбраны по условию.
Третий вид алгоритмов (с циклами) обеспечивает многократное выполнение некоторой совокупности действий. Например, для вычисления разности двух чисел в столбик необходимо сначала вычесть последние цифры исходных чисел и записать последнюю цифру результата (если требуется, перенести единицу из предыдущего разряда). Затем аналогично следует вычислить разность предпоследних цифр чисел и так далее. Процедура повторяется, пока все цифры исходных чисел не будут исчерпаны. Количество повторений зависит от количества цифр в заданных числах.
Алгоритм, предписывающий повторное выполнение действий, называется циклическим алгоритмом (алгоритмом с повторением, или структурой цикла).
Повторяемое действие или группа действий называется телом цикла. Количество повторений тела цикла определяется поставленным условием, которое называется условием цикла. По результату проверки условия осуществляется выбор: еще раз повторить тело цикла или перейти к другим действиям.
Наличие возврата к ранее произведенным действиям является характерным отличием алгоритмов с циклами от линейных и разветвленных.
Линейные алгоритмические конструкции
В блок–схемах линейные алгоритмы представляют с помощью последовательности функциональных блоков:
В алгоритмическом языке линейным структурам соответствует последовательность команд языка:
Команда 1
Команда 2
Команда 3
У линейной структуры только один вход и только один выход, попасть извне в середину выполняемой последовательности команд невозможно.
Пример 1. Определить значение целой переменной n после выполнения следующего алгоритма:
m := 3
n := 4
m := 6 + m*n
n := n + m/3
Решение. Первые две команды присваивания определяют начальные значения переменных. Для выполнения третьей команды сначала надо вычислить правую часть выражения: 6 + 3 х 4 = 18. Это значение будет присвоено переменной m. Для выполнения последней команды также сначала вычисляется правая часть выражения: 4 + 18/3 = 10. Результат будет присвоен переменной п.
Ответ: 10.
Даже для решения простых задач, ход которого не изменяется в зависимости от исходных данных, могут существовать разные варианты алгоритмов простой линейной структуры.
Пример 2. Вычислить значение выражения x2 – 3 × х – 10, используя только операции сложения и умножения.
Для решения задачи в той последовательности, что определяет само выражение, потребуется 2 операции умножения, 2 вычитания и 3 переменных (х, y, z). Однако можно вычислить то же выражение как (х — 2) × х – 10. Такой алгоритм расчета потребует 1 умножение, 2 вычитания и 2 переменных (х, у).
Решение.
Алгоритмические конструкции ветвления
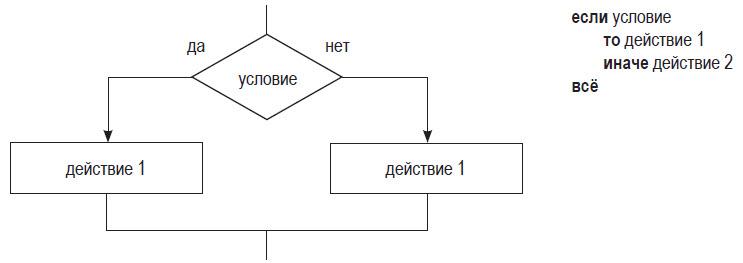
Для отображения базовой алгоритмической конструкции ветвления в блок–схемах используется альтернативный (условный) блок (фигура ромб), а в алгоритмических языках — команда если.
Существует две реализации структуры ветвления: полная и неполная (краткая). Обе формы ветвления являются замкнутыми: каждая из них имеет один вход и один выход.
Полная форма ветвления означает, что осуществляется выбор между двумя действиями. Если проверка условия дает результат «да», то выбирается действие 1; в противоположном случае (то есть если проверка условия дает результат «нет») — выбирается действие 2.
Таким образом, полная форма команды если определяет две ветви команд: первая выполняется, если условие истинно, вторая — если условие ложно. Каждая ветвь в итоге ведет к общему выходу, так что работа алгоритма будет продолжаться при выборе любого пути.
Пример 3. Для извлечения квадратного алгебраического корня из числа B необходимо проверить, положительно ли это число. Если проверка дает значение «истина» («да»), извлечь корень; если результат проверки — «ложь» («нет»), выдать соответствующее сообщение пользователю.

Краткая форма ветвления предполагает, что в случае истинности условия будет выполнена команда 1, а иначе — никакие действия не выполняются.
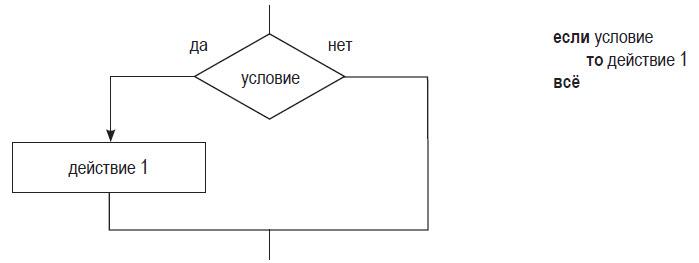
Пример 4. Для расчета значений гиперболы по формуле y = 2/x необходимо проверить, что значение х не равно нулю. Если проверка условия дает значение «истина», — вычислить результат. В противном случае (если проверка условия дает значение «ложь», т. е. х равно нулю) — не выполнять никаких действий, поскольку деление на ноль запрещено.
если 2/х ≠ 0
то y := 2/x
всё
Пример 5. Для приведенного фрагмента блок–схемы алгоритма выбрать соответствующий ему фрагмент на алгоритмическом языке.
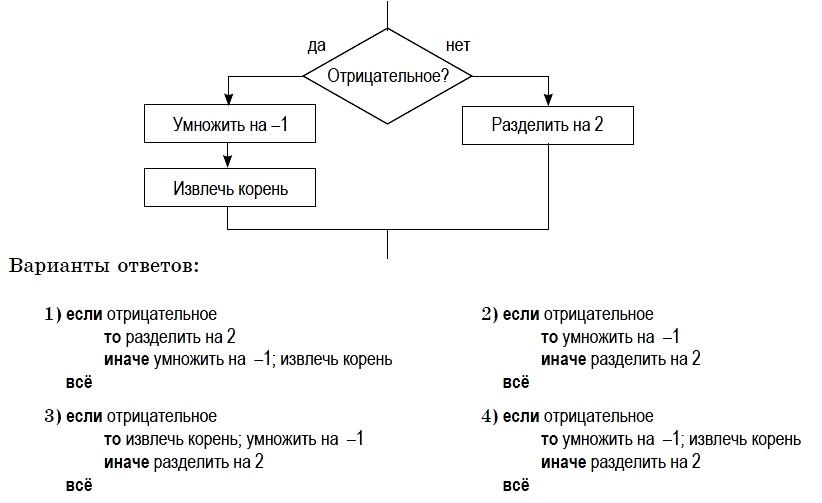
Решение. Ромбу на блок–схеме соответствует структура ветвление (команда если): проверяется условие «отрицательное». Если условие истинно, выполняется ветвь «да» (строка то на алгоритмическом языке) с двумя действиями: «умножить на –1»; «извлечь корень». Если условие ложно, выполняется ветвь «нет» (строка иначе на алгоритмическом языке) с одним действием: «разделить на 2». После обоих вариантов структура завершается, что соответствует служебному слову всё. Такому положению соответствует вариант алгоритма 4.
Ответ: 4.
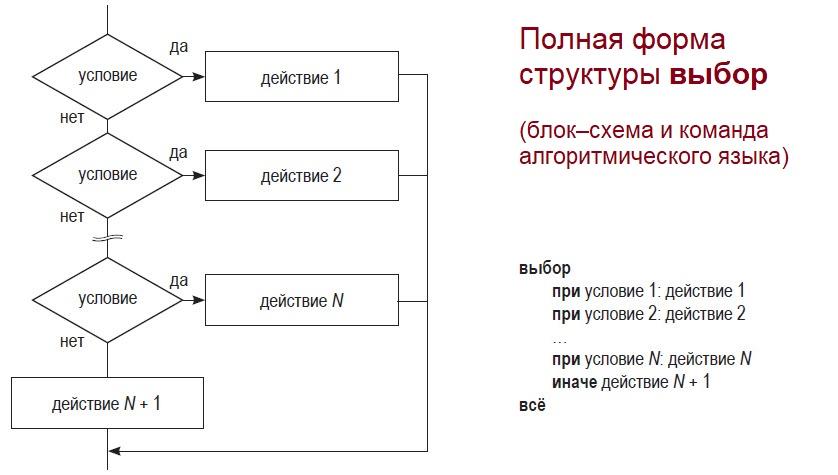
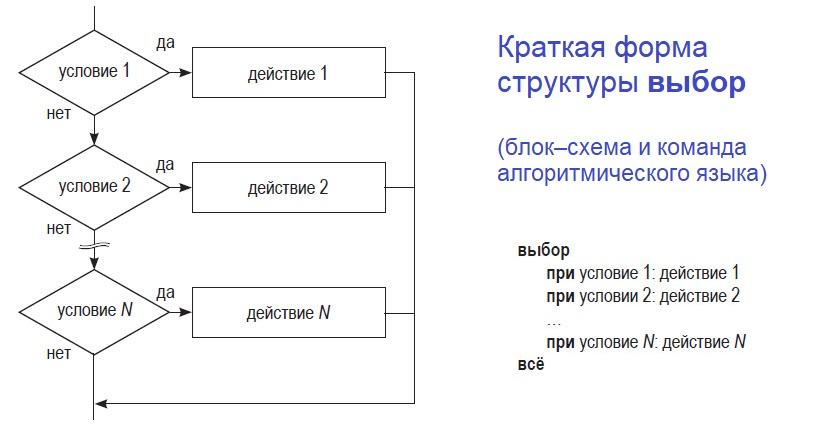
Для серии команд ветвления, следующих одна за другой (множественное ветвление), в алгоритмических языках существуют специальная команда выбор. Она также имеет полную и неполную (краткую) формы.
Структура ветвления выбор предполагает поочередную проверку нескольких условий (одно за одним). Если проверяемое условие 1 истинно, выполняется команда 1, если нет — переходят к проверке следующего условия. Если второе условие истинно — выполняется команда 2, если нет — проверяют следующее условие и т. д.
Полная и краткая формы структуры выбор различаются действиями после проверки последнего условия. Если проверка последнего условия выдает «ложь» («нет»), — в полной форме выполняют заданную команду; в краткой форме ничего не делают.
Во всех формах структур ветвления важную роль играют условия выбора. Часто в них используются операторы сравнения или другие отношения. Результатом условия может быть только одно из двух логических значений — Ложь или Истина. В языках программирования эти значения обычно записывают как True и False. В учебном алгоритмическом языке используют чаще значения «да» и «нет». В компьютерной форме эти значения обычно представлены битовыми значениями 0 и 1.
Простые условия обычно содержат только одну операцию — например, X 0, А ≠ В или s = «отец». Объединение нескольких простых условий образует составное условное выражение (или составное условие). Для объединения простых условий используются логические операторы:
and (логическое И),
or (логическое ИЛИ),
xor (исключающее ИЛИ),
not (отрицание).
Например, чтобы задать условие принадлежности числовой величины Z промежутку (10;20), следует записать составное условие Z 10 and Z
Циклические конструкции
Базовая структура цикл (или повторение) обеспечивает многократное выполнение одних и тех же команд. Существует несколько разновидностей циклических структур. Любая из них содержит тело цикла (набор повторяющихся команд) и заголовок цикла, который определяет количество повторений тела цикла.
ЦИКЛ С ПРЕДУСЛОВИЕМ (ИЛИ ЦИКЛ «ПОКА»)
Заголовок этой структуры содержит условие, которое называется предусловием. Эта структура предписывает повторять тело цикла до тех пор, пока выполняется условие в его заголовке (т. е. пока оно остается истинным).
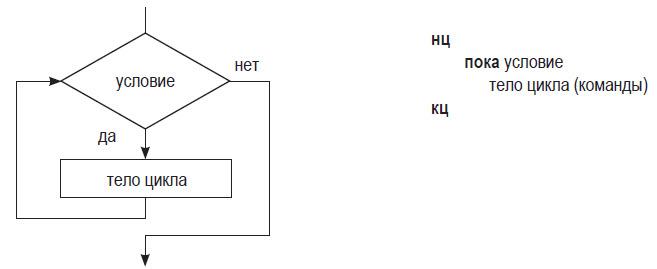
Работа цикла с предусловием начинается с проверки условия в его заголовке. Если условие истинно — выполняются команды тела цикла и происходит возврат к заголовку цикла. Снова проверяется условие заголовка (поскольку оно могло измениться в результате работы команд цикла) — если оно истинно, опять выполняется тело цикла. Так происходит до тех пор, пока проверка условия в заголовке не выдаст результат «нет». Тогда управление будет передано команде, следующей непосредственно за циклом.
Возможна ситуация, когда команды тела цикла не будут выполнены ни разу — если условие в заголовке сразу же выдает результат проверки «нет». Также возможна ситуация, когда условие заголовка всегда выдает положительный результат проверки — это приведет к бесконечному выполнению цикла, так называемому «зацикливанию» алгоритма. Таким образом, при создании цикла «пока» следует обращать особое внимание на формулировку условия в его заголовке.
Пример 6. Записать на алгоритмическом языке алгоритм получения остатка от деления целого числа а на целое число b с помощью вычитания.
Решение. Если число а меньше b, то остатком от деления служит само число а. В ином случае необходимо вычитать b из числа а до тех пор, пока результат не станет меньше b — он и будет остатком от деления.
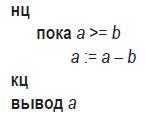
ЦИКЛ С ПОСТУСЛОВИЕМ (ИЛИ ЦИКЛ «ДО»)
Постусловие формулируется противоположным образом по отношению к предусловию. Цикл «до» предписывает повторять команды тела цикла до тех пор, пока не выполнится условие в его заголовке (т. е. пока оно остается ложным).
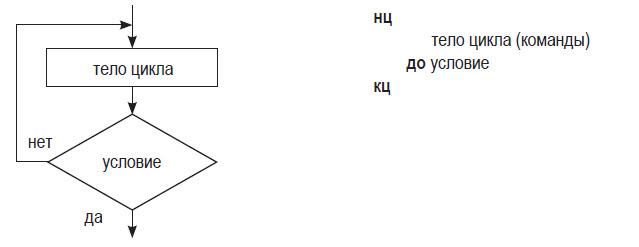
Работа цикла с постусловием начинается с выполнения команд тела цикла. Затем проверяется условие цикла. Если условие ложно (проверка условия дает результат «нет») — происходит возврат к выполнению команд тела цикла. Затем снова проверяется условие (поскольку оно могло измениться в результате работы команд цикла). Так происходит до тех пор, пока проверка условия не выдаст результат «да». Тогда происходит выход из цикла и управление будет передано команде, следующей непосредственно за циклом.
В отличие от цикла с предусловием, тело цикла «до» всегда выполняется хотя бы один раз (до первой проверки). Тело цикла «пока» может не выполниться ни разу, если условие при первой же проверке выдаст «нет». Поэтому цикл с постусловием можно заменить циклом с предусловием, а наоборот — нет.
Пример 7. Записать алгоритм примера 6 с помощью цикла «до».
Решение.
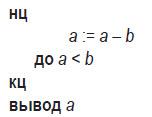
ЦИКЛ С ПАРАМЕТРОМ (ЦИКЛ СО СЧЕТЧИКОМ, ИЛИ ЦИКЛ «ДЛЯ»)
Эта структура предписывает повторять команды тела цикла для всех значений некоторой переменной (параметра, или счетчика цикла).
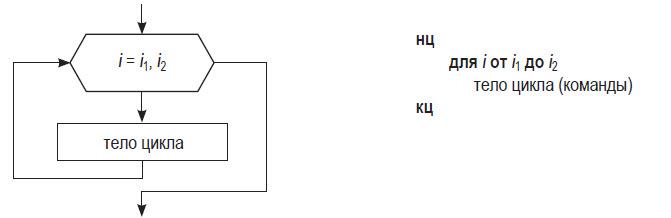
Имя параметра цикла (счетчика) указывают в заголовке после служебного слова для. Затем с помощью служебных слов от и до задают начальное и конечное значение этого параметра.
Работа цикла «для» начинается с присвоения параметру начального значения. Если оно не превышает конечного значения, выполняются команды тела цикла. Затем значение параметра цикла увеличивается на единицу. Если оно снова не превышает конечного значения, опять происходит выполнение тела цикла. Если же полученное значение параметра превысит конечное, цикл будет завершен и управление передано следующей за циклом команде.
Цикл со счетчиком всегда выполняется i1 – i2 + 1 раз.
Пример 8. Записать алгоритм вычисления факториала числа N.
Решение. Факториал числа вычисляется по формуле N! = 1 × 2 × … × N. Следовательно, для расчета факториала надо организовать цикл со счетчиком, в котором перемножить последовательные целые числа от 2 до N. Значение 1!, равное 1, можно присвоить результирующей переменной до цикла.

Понятие программы. Программирование и его виды
Программа – это последовательность инструкций (команд), описывающая алгоритм решения с помощью компьютера соответствующей задачи, для реализации которой эта программа была разработана.
Для разработки программ используются специальные языки.
Программа может содержать инструкции, написанные на языках программирования высокого уровня (ЯВУ), которые позволяют записать алгоритмы в удобной для понимания человеком форме, приближенной к естественным языкам (исходный код), или последовательность машинных команд (инструкций, «понятных» компьютеру, на котором данная программа должна выполняться).
Готовыми к выполнению являются только программы, содержащие инструкции в двоичном машинном коде, – программы на языке конкретного компьютера (компьютера с процессором определенной модели или семейства), только такие программы можно загрузить в память компьютера для выполнения. Таким образом, программы в машинном коде не являются «переносимыми», их можно выполнять только на компьютерах с общей архитектурой, системой команд, поддерживаемой этими компьютерами, т.е. одинаковым машинным языком.
Исходный код программы на языке программирования создает программист, используя при этом имеющиеся в его распоряжении редакторы текстов (специальные программы, которые используются для ввода и модификации текстовой информации). Для перевода программы, написанной на языке программирования, в форму, готовую к выполнению (в машинный код), используются специальные системные программы (трансляторы, компоновщики), которые помогают программисту разработать программу. Разработчики применяют различные инструментальные средства, входящие в состав систем программирования, снижающие трудоемкость разработки программ. Современные системы программирования включают в свой состав текстовые редакторы, средства визуального программирования, трансляторы с определенных языков программирования, компоновщики, позволяющие «собрать» программы из отдельно разработанных модулей, и средства отладки программ, позволяющие выявлять и исправлять ошибки в процессе разработки программы.
Все программы хранятся в файлах на дисках компьютера. Тип файла определяет способ записи программы в нем. При загрузке программы в память на выполнение она считывается из файла и записывается в выделенную ей для выполнения оперативную память с помощью специальной программы загрузки, так как процессор может прочитать и выполнить только команды, находящиеся в оперативной памяти компьютера.
Таким образом, кроме программ, решающих задачи пользователя, существуют и программы, выполняющие вспомогательные, обслуживающие функции, позволяющие повысить эффективность и снизить трудоемкость работы.
Процесс создания программы называется программированием.
Выделяют несколько разновидностей программирования.
Алгоритмическое или модульное
Основная идея алгоритмического программирования – разбиение программы на последовательность модулей, каждый из которых выполняет одно или несколько действий. Единственное требование к модулю – чтобы его выполнение всегда начиналось с первой команды и всегда заканчивалось на самой последней (то есть чтобы нельзя было попасть на команды модуля извне и передать управление из модуля на другие команды в обход заключительной).
Алгоритм на выбранном языке программирования записывается с помощью команд описания данных, вычисления значений и управления последовательностью выполнения программы.
Текст программы представляет собой линейную последовательность операторов присваивания, цикла и условных операторов. Таким способом можно решать не очень сложные задачи и составлять программы, содержащие несколько сот строк кода. После этого понятность исходного текста резко падает из-за того, что общая структура алгоритма теряется за конкретными операторами языка, выполняющими слишком детальные, элементарные действия. Возникают многочисленные вложенные условные операторы и операторы циклов, логика становится совсем запутанной, при попытке исправить один ошибочный оператор вносится несколько новых ошибок, связанных с особенностями работы этого оператора, результаты выполнения которого нередко учитываются в самых разных местах программы.
Структурное программирование
При создании средних по размеру приложений (несколько тысяч строк исходного кода) используется структурное программирование, идея которого заключается в том, что структура программы должна отражать структуру решаемой задачи, чтобы алгоритм решения был ясно виден из исходного текста. Для этого надо иметь средства для создания программы не только с помощью трех простых операторов, но и с помощью средств, более точно отражающих конкретную структуру алгоритма. С этой целью в программирование введено понятие подпрограммы – набора операторов, выполняющих нужное действие и не зависящих от других частей исходного кода. Программа разбивается на множество мелких подпрограмм (занимающих до 50 операторов – критический порог для быстрого понимания цели подпрограммы), каждая из которых выполняет одно из действий, предусмотренных исходным заданием. Комбинируя эти подпрограммы, удается формировать итоговый алгоритм уже не из простых операторов, а из законченных блоков кода, имеющих определенную смысловую нагрузку, причем обращаться к таким блокам можно по названиям. Получается, что подпрограммы – это новые операторы или операции языка, определяемые программистом.
Возможность применения подпрограмм относит язык программирования к классу процедурных языков.
Наличие подпрограмм позволяет вести проектирование и разработку приложения сверху вниз – такой подход называется нисходящим проектированием. Сначала выделяется несколько подпрограмм, решающих самые глобальные задачи (например, инициализация данных, главная часть и завершение), потом каждый из этих модулей детализируется на более низком уровне, разбиваясь, в свою очередь, на небольшое число других подпрограмм, и так происходит до тех пор, пока вся задача не окажется реализованной.
Такой подход удобен тем, что позволяет человеку постоянно мыслить на предметном уровне, не опускаясь до конкретных операторов и переменных. Кроме того, появляется возможность некоторые не реализовывать сразу подпрограммы, а временно откладывать, пока не будут закончены другие части. Например, если имеется необходимость вычисления сложной математической функции, то выделяется отдельная подпрограмма такого вычисления, но реализуется она временно одним оператором, который просто присваивает заранее выбранное значение. Когда все приложение будет написано и отлажено, тогда можно приступить к реализации этой функции.
Немаловажно, что небольшие подпрограммы значительно проще отлаживать, что существенно повышает общую надежность всей программы.
Очень важная характеристика подпрограмм – это возможность их повторного использования. С интегрированными системами программирования поставляются большие библиотеки стандартных подпрограмм, которые позволяют значительно повысить производительность труда за счет использования чужой работы по созданию часто применяемых подпрограмм.
Подпрограммы бывают двух видов – процедуры и функции. Отличаются они тем, что процедура просто выполняет группу операторов, а функция вдобавок вычисляет некоторое значение и передает его обратно в главную программу (возвращает значение). Это значение имеет определенный тип (говорят, что функция имеет такой-то тип).
Подпрограммы решают три важные задачи:
• избавляют от необходимости многократно повторять в тексте программы аналогичные фрагменты;
• улучшают структуру программы, облегчая ее понимание;
• повышают устойчивость к ошибкам программирования и непредвидимым последствиям при модификациях программы.
Объектно-ориентированное программирование
В середине 80-х годов в программировании возникло новое направление, основанное на понятии объекта. До того времени основные ограничения на возможность создания больших систем накладывала разобщенность в программе данных и методов их обработки.
Реальные объекты окружающего мира обладают тремя базовыми характеристиками: они имеют набор свойств, способны разными методами изменять эти свойства и реагировать на события, возникающие как в окружающем мире, так и внутри самого объекта. Именно в таком виде в языках программирования и реализовано понятие объекта как совокупности свойств (структур данных, характерных для этого объекта), методов их обработки (подпрограмм изменения свойств) и событий, на которые данный объект может реагировать и которые приводят, как правило, к изменению свойств объекта.
Появление возможности создания объектов в программах качественно повлияло на производительность труда программистов. Максимальный объем приложений, которые стали доступны для создания группой программистов из 10 человек, за несколько лет увеличился до миллионов строк кода, при этом одновременно удалось добиться высокой надежности программ и, что немаловажно, повторно использовать ранее созданные объекты в других задачах.
Объекты могут иметь идентичную структуру и отличаться только значениями свойств. В таких случаях в программе создается новый тип, основанный на единой структуре объекта. Он называется классом, а каждый конкретный объект, имеющий структуру этого класса, называется экземпляром класса.
Объектно-ориентированный язык программирования характеризуется тремя основными свойствами:
1. Инкапсуляция – объединение данных с методами в одном классе;
2. Наследование – возможность создания на основе имеющегося класса новые классы с наследованием всех его свойств и методов и добавлением собственных;
3. Полиморфизм – присвоение действию одного имени, которое затем совместно используется вниз и вверх по иерархии объектов, причем Каждый объект иерархии выполняет это действие способом, подходящим именно ему.