Разработка открытого урока по геометрии в 7 классе на тему "Задачи на построение с помощью циркуля и линейки"

Разработка открытого урока по геометрии в 7 классе

на тему: "Задачи на построение с помощью циркуля и линейки"

Учитель математики специализированной школы № 6

Сергелийского района г. Ташкента

Хамидханова Гулшан Тажибековна

Цели урока:  

образовательные:

1. формирование умений учащихся циркулем и линейкой без деления выполнять задачи на построение, а именно: находить середину отрезка; строить перпендикулярные прямые; проводить биссектрису угла; строить угол, равный данному;

2. формирование умений учащихся в применении признаков  равенства треугольников для обоснования построения.

      Развивающие задачи:

1. развитие  умений учащихся  самостоятельно работать с учебником;

2. развитие способностей анализа и синтеза у учащихся.

 Воспитательные задачи:

1. воспитание уважения учащихся друг к другу, уважения к чужому труду, к мыслям;

2. формирование интереса к предмету, к данной теме;

3. воспитание аккуратности при построении чертежей.

Учебная цель (обобщающая): учащиеся усваивают алгоритмы, чтобы  применять их в типовых ситуациях. 

 Структура урока в соответствии с рекомендациями «Дарс – мукаддас»:

1. Оргмомент, активизацию мыслительно-познавательной деятельности учащихся (3 мин).

2. Проверка выполнения домашнего задания, решение тестов (7 мин)( приложение к уроку)

3. Третья часть урока – изучение нового материала (15мин). Консультанты групп объясняли всем учащимся класса алгоритм выполнения построения своей задачи. Перед группой, которая защищала свою задачу, стоял проблемный вопрос: как обосновать справедливость своего построения, применяя признаки равенства треугольников. На этом этапе применялись интерактивные технологии.

4. Закрепление изученного материала: решение задач из учебника ( 15 мин).

5. Пятый этап урока: рефлексия учащихся (5 мин). Учащиеся отвечают на вопросы, чему они научились на уроке, а на что надо еще обратить внимание, заполняют таблицу рефлексии.

6. Домашнее задание, рекомендации учителя. Оценивание активных учащихся

Формы работы учащихся–

групповая работа в статистических парах,  при проверке  знаний и умений в выполнении домашней задачи на построение;  

индивидуальная – при выполнении построений в тетрадях, интерактивная – при изучении алгоритмов задач на построение.

Вид урока:  проблемно – поисковый

Тип урока: интерактивный .

Технологии, которые применяются на уроке:

1. ИКТ технологии;

2. Технологии работы в статистических парах.

Ход урока:

1. Оргмомент:

приветствие, выявить отсутствующих учащихся и причину отсутствия:

актуализация ранее полученных знаний

1. Проверка выполнения домашнего задания, разбор наиболее трудных задач ( по желанию учащихся).

2. Изучение нового материала:

Наша задача – выполнить задачи на построение только с помощью двух инструментов: циркуля и линейки без масштабных делений.

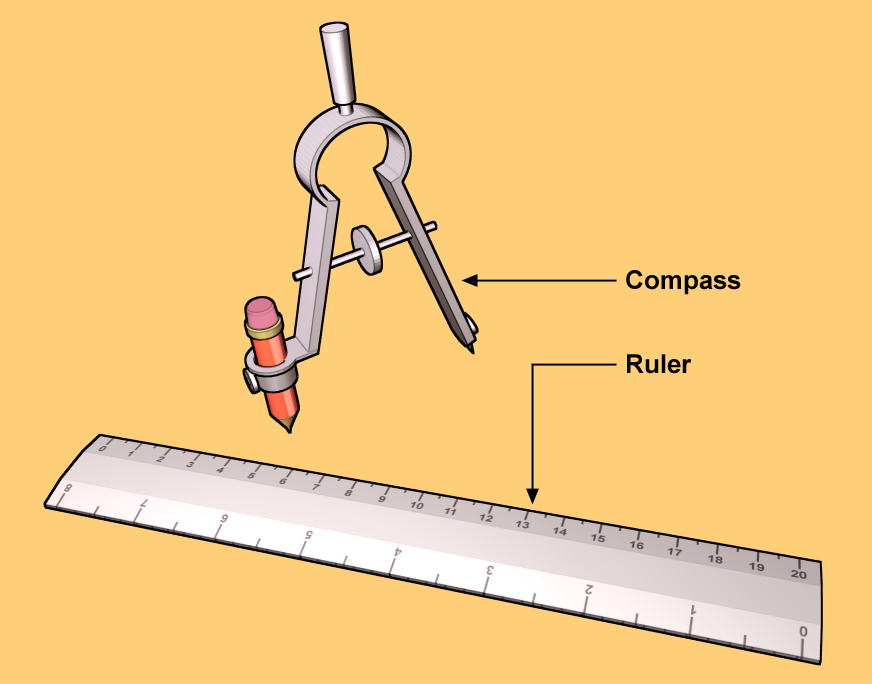
линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки.

Циркуль позволяет провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку (приложение № 1).

Проблемный вопрос: как начертить окружность без циркуля?

Ответ - показать на слайде

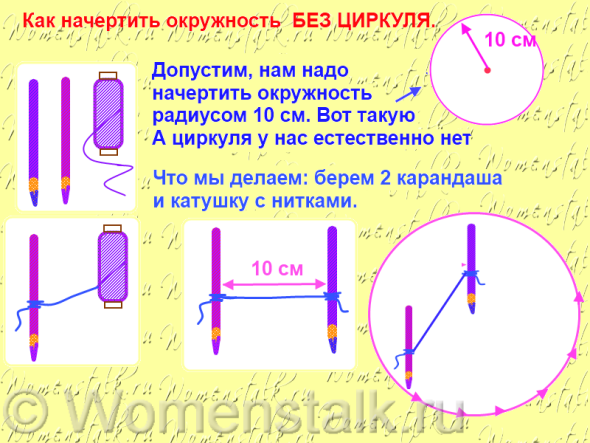
Выполняя эти несложные операции, мы сможем решить много интересных задач на построение :

1. На данном луче от его начала отложить отрезок, равный данному.

2. Отложить от данного луча угол, равный данному.

3. Построить биссектрису данного неразвернутого угла( приложение № 2)

4. Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.

5. Построить середину данного отрезка.

Просмотр видео роликов ( №1, №2, №3)позволяет разобрать некоторые базовые задачи и самостоятельно повторить их в тетради.

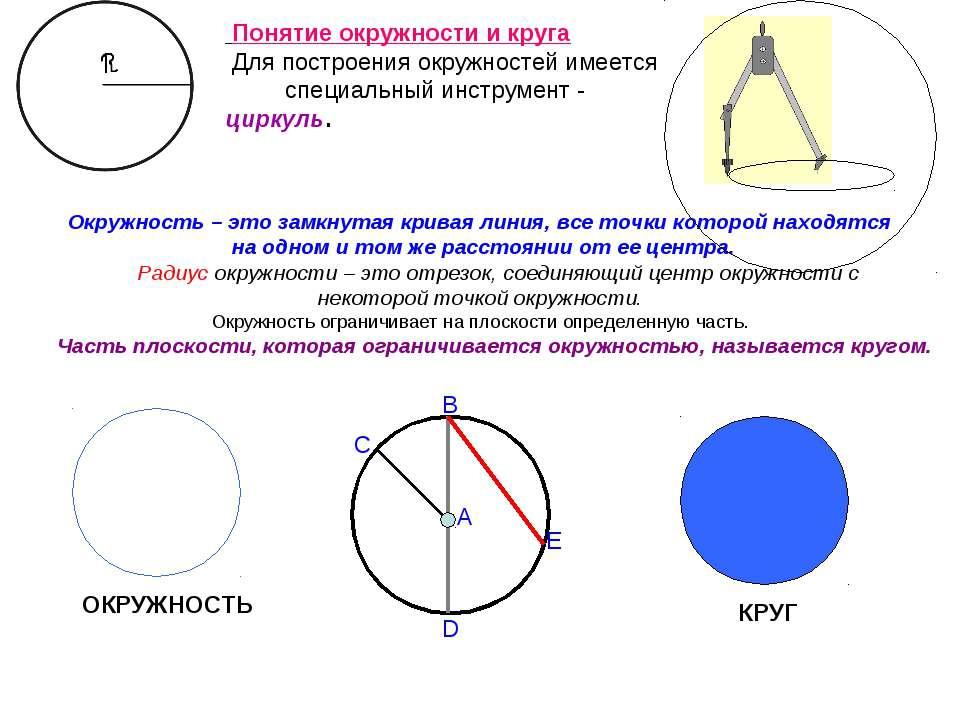
А теперь обратимся к истории геометрии. Древнегреческие математики достигли чрезвычайно большого искусства в геометрических построениях с помощью циркуля и линейки. Они доказали, что угол можно разделить и на четыре равных угла. Для этого нужно разделить его пополам, а затем построить биссектрису каждой половинки. А можно ли с помощью циркуля и линейки разделить угол на три равные части? Эта задача, получившая название задачи о трисекции угла, в течение многих веков привлекала внимание математиков. Однако она не поддавались их усилиям. Лишь в прошлом веке было доказано, что для произвольного угла такое построение невозможно.

Есть и другие задачи на построение, про которые известно, что они неразрешимы с помощью циркуля и линейки. Я предлагаю вам самостоятельно найти материал, содержащий информацию для ознакомления с этими задачами.

рефлексия учащихся (5 мин). Учащиеся отвечают на вопросы, чему они научились на уроке, а на что надо еще обратить внимание, заполняют таблицу рефлексии.

1. Рекомендации к выполнению домашнего задания: стр 132 № 6, № 7 ( а, в, д), стр 133 № 2, № 3 (а,в).

Подведение итогов урока – оценивание активных учащихся