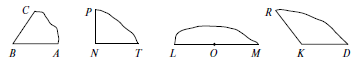Разработка урока № 1 "Измерение углов. Транспортир" (5 класс, учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков и др.)

У р о к № 1. Измерение углов. Транспортир

Основная дидактическая цель урока: познакомить учащихся с транспортиром, учить измерять углы с помощью транспортира.

Х о д у р о к а

I. Организационный момент

II. Устный счёт

(Работа на листочках.)

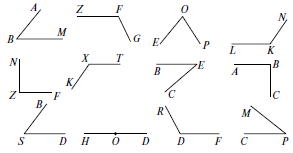
– Какие из углов, изображённых на рисунке, являются:

а) острыми;

б) тупыми;

в) есть ли среди этих углов прямые?

III. Определение темы урока

Мы знаем, что два угла можно сравнивать друг с другом.

– Какой способ для этого мы использовали?

Но углы, так же как и отрезки, можно сравнивать не только наложением, но и с помощью измерения. Как называется данный прибор, вы узнаете, отгадав кроссворд.

Кроссворд.

(Фронтальная работа. Работа на листочках.)

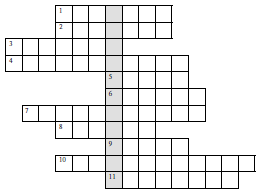
1) Результат деления. (Частное.)

2) Лучи, образующие угол. (Стороны.)

3) Точка, из которой выходят лучи, образующие угол. (Вершина.)

4) Угол, который образуют два дополнительных друг другу луча. (Развёрнутый.)

5) Результат сложения. (Сумма.)

6) Угол, который составляет половину развёрнутого угла. (Прямой.)

7) Инструмент, который используют для построения прямого угла. (Треугольник.)

8) Угол меньше прямого. (Острый.)

9) Угол больше прямого, но меньше развёрнутого. (Тупой.)

10) Результат умножения. (Произведение.)

11) Результат вычитания. (Разность.)

(В выделенном столбце: транспортир.)

IV. Работа по теме урока

– Какую форму напоминает транспортир? (Полукруг.)

– На сколько частей или градусов разделён транспортир? (180.)

– Что ещё есть у всех транспортиров? (Центр.)

Центр ещё является вершиной развёрнутого угла. У некоторых транспортиров есть ещё двойная шкала.

– Для чего нам нужна двойная шкала? (Позволяет более точно измерять и строить углы.)

– Используя рис. 7.14 на с. 154, мы попробуем составить алгоритм измерения углов.

1. Одна сторона угла должна проходить через нулевую отметку (0° по шкале).

2. Вторая сторона угла должна пересекать шкалу. Нужно посмотреть, через какую отметку проходит вторая сторона угла. Это и есть величина этого угла.

3. Нужно вершину угла совместить с центром транспортира.

V. Работа по учебнику

1. С. 154, № 7.57.

– Что значит «в порядке возрастания»?

Ответ:

а) ∠TZO, ∠TZM, ∠TZL;

б) ∠KZL, ∠KZM, ∠KZN, ∠KZO;

в) ∠OZN, ∠NZM, ∠OZM, ∠NZL, ∠OZL.

– Определите по записям, какие из углов тупые (∠TZM, ∠TZL, ∠KZN, ∠KZO, ∠NZL, ∠OZL), какие острые (∠TZO, ∠KZL, ∠KZM, ∠OZN, ∠NZM, ∠OZM).

– Какие из углов равны половине прямого? (Таких углов нет.)

2. С. 154, № 7.58 (работа в паре).

3. С. 155, № 7.60.

(45° + 27° = 72°.)

VI. Повторение изученного материала

С. 156, № 7.70 (устно).

– Какие углы прямые? (CBA, ZQV, XQZ, XQY, YQV.)

– Какие углы развёрнутые? (TOS, MOK, NOL, ZQY, XQV.)

VII. Работа в рабочей тетради

С. 42, № 1, 2, 3.

– Заполните пропуски в каждом задании.

VIII. Практическая работа

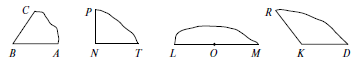
– Выберите из предложенных вам углов острый, тупой, прямой, развёрнутый.

– Измерьте их градусную меру и запишите эти данные.

– Сделайте вывод о градусной мере:

а) развёрнутого угла;

б) прямого угла;

в) острого угла;

г) тупого угла.

IX. Рефлексия

– Что нового вы сегодня узнали на уроке?

Домашнее задание

С. 156, № 7.73, 7.75.