Разработка урока № 1 "Сравнение десятичных дробей" (5 класс, учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков и др.)

У р о к № 1. Сравнение десятичных дробей

Основная дидактическая цель урока: познакомить учащихся с алгоритмом сравнения десятичных дробей, учить выполнять сравнение с опорой на алгоритм.

Х о д у р о к а

I. Организационный момент

II. Устная работа

– Выясните, в каком столбике верно записано число. Напишите в кружке соответствующую ему букву.

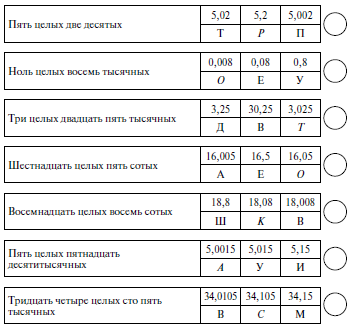
– Какое слово вы прочитали? (Ротокас.)

«Ротокас» – это название самого короткого в мире алфавита. В нём всего 11 букв, он используется жителями Папуа – Новой Гвинеи.

– Сколько букв содержит русский алфавит? (33.)

III. Работа по теме урока

На доске запись:

3,1 3,91 3, 278 3,2 3,001

– Что записано на доске? (Десятичные дроби.)

– Что вы можете о них сказать? (Это десятичные дроби, целая часть в этих дробях равна 3.)

– Запишите дроби в порядке возрастания.

(Двое учащихся работают у доски.)

– Что у вас получилось?

– Какие затруднения у вас возникли?

– Итак, кто может сформулировать тему сегодняшнего урока? («Сравнение десятичных дробей».)

– Сравните дроби.

3,1 и 13,1

3,1 и 3,3

3,11 и 3,14

3,11 и 3,4

– Какие есть мысли по поводу сравнения первой пары чисел?

– Количество целых у второй дроби больше, чем у первой, значит, 13,1 3,1.

– Какой вывод можно сделать? (Сначала смотрим на количество целых. Больше будет та дробь, у которой больше целых.)

– Сравниваем вторую пару дробей, сначала целые части.

– Целых одинаковое количество, но десятых у второй дроби больше, чем у первой, значит, 3,1 3,3.

– Сделайте вывод. (Если целых одинаковое количество, смотрим на десятые, больше будет та дробь, у которой десятых больше.)

– Сравните третью пару дробей и сделайте вывод. (Если целых и десятых одинаковое количество, смотрим на сотые, больше будет та дробь, у которой сотых больше.)

– Какая дробь будет больше? (3,11 3,14.)

– Как сравнить 3,11 и 3,4?

– У числа 3,4 количество десятых больше, чем у числа 3,11, значит, 3,4 3,11.

– Давайте попробуем убедиться в этом. Сравним десятичные дроби 3,11 и 3,4.

1) Уравняем число десятичных знаков: 3,11 и 3,40.

2) Отбросим запятую: 311 и 340.

3) Сравним получившиеся натуральные числа: 311 340.

4) Сделаем вывод: 3,11 3,4.

IV. Работа по учебнику

1. С. 99, № 6.34.

76,07 и 87,88 (.)

38,9 и 38,9000 (=.)

0,5 и 0,637 (.)

0,834 и 0,843 (.)

8,6442 и 8,6433 (.)

0,0057 и 0,00567 (.)

2. С. 99, № 6.35.

(8,175; 8,057; 5,487; 5,478; 1,321.)

(0,0023; 0,0055; 0,0081; 0,073; 0,09.)

3. С. 99, № 6.39.

4. С. 99, № 6.40 (работа в паре).

Ответ: вместо знака вопроса можно поставить цифры:

а) 1, 2, 3, 4, 5, 6, 7, 8, 9;

б) 6, 7, 8, 9.

V. Повторение изученного материала

С. 101, № 6.56 (1, 2).

– Как вы понимаете выражение «вверх по реке»? (Направления скоростей катера и течения реки не совпадают.)

– Что будет происходить с собственной скоростью катера? (Скорость течения реки будет мешать движению лодки.)

– Как решать задачу в этом случае?

– Решите задачу.

– Прочитайте ответ. (66 км прошёл катер.)

– Прочитайте вторую задачу.

– Как вы понимаете выражение «вниз по течению»? (Направление движения воды в реке и направление движения теплохода совпадают.)

– Если при движении вниз по течению теплоход выключит собственную скорость, с какой скоростью он будет двигаться? (Со скоростью течения.)

– Из чего же будет складываться скорость теплохода при движении вниз по течению? (Собственная скорость теплохода + скорость течения.)

– Решите задачу.

– Прочитайте ответ. (Теплоход прошёл 158 км.)

На доске запись:

v_{по течению} = v_{собственная} + v_{течения}

v_{против течения} = v_{собственная} - v_{течения}

– Как найти собственную скорость, если известны скорость по течению и скорость течения реки?

– Как узнать скорость течения, если известны скорость по течению и собственная скорость?

– Как найти собственную скорость, если известны скорость против течения и скорость течения?

VI. Рефлексия

– Изменится ли десятичная дробь, если в конце её приписать нуль? 6 нулей?

– Сформулируйте правило сравнения десятичных дробей.

Домашнее задание

С. 101, № 6.61, 6.62, 6.65.