Разработка урока № 1 "Степень с натуральным показателем" (5 класс, учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков и др.)

У р о к № 1. Степень с натуральным показателем

Основная дидактическая цель урока: познакомить учащихся с возведением числа в степень, познакомить с понятиями «квадрат числа» и «куб числа», продолжить работу над текстовыми задачами.

Х о д у р о к а

I. Организационный момент

II. Устный счёт

– Найдите сходство и различие в примерах.

– Разделите выражения на группы и укажите, по какому принципу вы их разделили.

4 + 4 + 4

5 ・ 5 ・ 5 ・ 5

7 ・ 7

7 + 7 + 7 + 7

10 ・ 10 ・ 10

2 + 2 + 2 + 2 + 2 + 2 + 2

Сумму одинаковых слагаемых можно представить в виде произведения.

4 + 4 + 4 = 4 ・ 3 = 12

7 + 7 + 7 + 7 = 7 ・ 4 = 28

2 + 2 + 2 + 2 + 2 + 2 + 2 = 2 ・ 7 = 14

– А если я попрошу вас записать произведение 1000 одинаковых множителей, какое выражение получится?

– Удобно пользоваться такими длинными записями?

– А знаем ли мы способ, который позволит сделать эту запись короче?

III. Работа по теме урока

– Что означает число 7 в выражении 7 ・ 7? (Повторяющийся множитель.)

Можно записать это выражение по-другому: 7².

Обратите внимание, в записи 7² участвуют два числа, одно – повторяющийся множитель, число 7, другое, которое показывает количество множителей, – число 2, его записывают мелким шрифтом сверху и справа.

– Рассмотрим выражение: 5 ・ 5 ・ 5 ・ 5. Запишем его по-другому: 5⁴.

Обратите внимание, в записи 5⁴ участвуют два числа, одно – повторяющийся множитель, число 5, другое, которое показывает количество множителей, число 4, его записывают мелким шрифтом сверху и справа.

– Рассмотрим равенство: 10 ・ 10 ・ 10 = 10³.

В записи 10³ участвуют два числа: число 10, записанное обычным шрифтом, называется основанием степени, и число 3, записанное мелким шрифтом сверху и справа, называется показателем степени. Выражение 10³ называют степенью числа.

При чтении сначала называют основание степени, а потом показатель степени, то есть 10³ – это десять в степени три.

– Прочитайте два первых примера. (7² – семь в степени два; 5⁴ – пять в степени четыре.)

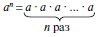
Степенью числа а с натуральным показателем n (n 1) называется произведение n множителей, каждый из которых равен а.

IV. Работа по учебнику

1. С. 113–114 (работа по статье учебника).

– Прочитайте статью учебника и приготовьтесь отвечать на вопросы.

– Квадрат числа в пределах 10 вычислить легко, это примеры из таблицы умножения. А вот квадраты чисел в пределах 20 помещены на втором форзаце учебника. Рассмотрите эту таблицу.

– Чему равен квадрат чисел 11, 13, 15, 19?

– Рассмотрите вторую таблицу.

– Что вы можете о ней сказать?

– Назовите куб чисел 3, 5, 8, 9.

2. С. 114, № 3.298.

(5⁶, 21⁵, 203³, 99⁴, 2018³,10¹⁰⁰.)

3. С. 114, № 3.300.

(t⁷, r⁴, a⁸, h², c⁵, a^p.)

4. С. 114, № 3.302.

Ответ:

8 ・ 8 ・ 8 ・ 8 ・ 8 ・ 8

13 ・ 13 ・ 13

1000 ・ 1000

50 ・ 50 ・ 50 ・ 50 ・ 50

x ・ x ・ x

a ・ a ・ a ・ a

b ・ b ・ b ・ b ・ b ・ b ・ b

n ・ n ・ n ・ n ・ n ・ n ・ n ・ n ・ n

5. С. 115, № 3.305.

(64, 100 000, 1, 81, 53, 243.)

6. С. 115, № 3.306.

(21, 29, 81, 41.)

V. Повторение изученного материала

С. 116, № 3.321 (устно).

VI. Работа над задачей

1. Для приготовления пирога берут 7 частей муки, 6 частей молока, 5 частей сахара, 2 части яиц. Сколько граммов муки, молока, сахара и яиц потребуется для приготовления 800 г пирога?

– Что вы можете сказать об этой задаче?

– Что следует обозначить буквой в задаче на части?

Пусть масса одной части будет х.

Тогда масса муки будет 7х.

Масса молока будет 6х.

Масса сахара будет 5х.

Масса яиц будет 2х.

Масса всего теста равна 7х + 6х + 5х + 2х.

В условии сказано, что масса теста 800 г.

Значит, можем составить уравнение:

7х + 6х + 5х + 2х = 800

20х = 800

х = 800 : 20

х = 40 (г) – масса одной части.

40 ・ 7 = 280 (г) – масса муки.

40 ・ 6 = 240 (г) – масса молока.

40 ・ 5 = 200 (г) – масса сахара.

40 ・ 2 = 80 (г) – масса яиц.

2. С. 116, № 3.324 (1) (работа в паре).

Пусть одно из чисел будет х.

Тогда второе будет 7х.

Сумма этих чисел равна х + 7х.

По условию сумма чисел равна 488.

Значит, можем составить уравнение:

х + 7х = 488

8х = 488

х = 488 : 8

х = 61 – одно из чисел.

61 ・ 7 = 427 – второе число.

– Как иначе можно найти второе число? (488 – 61 = 427.)

VII. Работа в рабочей тетради

С. 36, № 1 (устно), № 3.

VIII. Тест

В а р и а н т 1

1. Вычислите 8².

1) 64 2) 16 3) 2 4) 8

2. Вычислите 2 ・ 4³.

1) 24 2) 128 3) 512 4) 32

3. Упростите выражение 11а – а – 21.

1) 11а - 21 3) 3а

2) 8а 4) 10а - 21

4. Найдите значение выражения у³ – 2 при у = 6.

1) 16 2) 216 3) 214 4) 64

5. Упростите выражение 19 – (14 + с)

1) 5с 3) 33 – с

2) 5 + с 4) 5 – с

6. Вместо пропусков вставьте такую цифру, чтобы разность была верной.

–2874

945

1*2*

1) 9 2) 1 3) 0 4) 3

В а р и а н т 2

1. Вычислите 10³.

1) 30 2) 3 3) 10 4) 1000

2. Вычислите 3 ・ 5².

1) 45 2) 30 3) 225 4) 75

3. Упростите выражение 11у + у + 3.

1) 11у + 3 3) 14у

2) 12у + 3 4) 15у

4. Найдите значение выражения х² + 5 при х = 11.

1) 126 2) 121 3) 27 4) 256

5. Упростите выражение 15 – (b + 2).

1) 17 – b 3) 13b

2) 13 – b 4) 13 + b

6. Вместо пропусков вставьте такую цифру, чтобы разность была верной.

–3284

648

2*3*

1) 3 2) 7 3) 6 4) 4

Таблица для заполнения

IX. Рефлексия

– Какое новое знание вы получили сегодня на уроке?

– Как вы понимаете выражение «7 в кубе»?

– Вычислите: 6², 5², 7².

Домашнее задание

С. 116, № 3.326, 3.327, 3.329, 3.331.