Разработка урока № 1 "Свойства и признаки делимости" (5 класс, учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков и др.)

У р о к № 1. Свойства и признаки делимости

Основная дидактическая цель урока: изучить свойства делимости натуральных чисел, научиться их применять при решении задач.

Х о д у р о к а

I. Организационный момент

II. Устный счёт

С. 126, № 3.393 (а, б).

III. Работа по теме урока

– Разгадайте кроссворд.

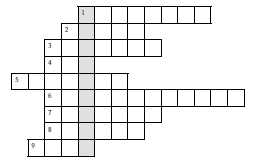
1) Чем является а в выражении b : a = c? (Делитель.)

2) Сколько будет два плюс два умножить на два? (Шесть.)

3) Математическое действие. (Деление.)

4) Частное от деления 24 на 8. (Три.)

5) Чем является b в выражении b : a = c? (Делимое.)

6) Результат умножения двух чисел. (Произведение.)

7) Чем является с в выражении b : a = c? (Частное.)

8) Чему равен делитель, если делимое равно 28, а частное – 7? (Четыре.)

9) На какое число нельзя делить? (Нуль.)

––Прочитайте слово в выделенном столбце. (Делимость.)

Тема нашего урока: «Свойства делимости». Мы узнаем, какие свойства делимости существуют, и постараемся научиться их применять.

– Как вы думаете, для чего нужны свойства делимости?

– Вспомним свойства деления.

0 : a = 0

На 0 делить нельзя.

а : 1 = а

а : а = 1.

– Для начала давайте вспомним, что значит разделить нацело натуральное число? (Натуральное число а делится нацело на натуральное число b, если существует натуральное число с, при умножении которого на b получается а: а = b ・ c.)

Свойство 1. Если один из множителей делится на некоторое число, то и произведение делится на это число.

– Рассмотрим пример.

– 15 делится на 3? (Да, т. к. 15 = 3 ・ 5.)

– 15 ・ 11 делится на 3? почему? (Да, т. к. один из множителей делится на 3.)

Свойство 2. Если первое число делится на второе, а второе делится на третье, то первое число делится на третье.

– Рассмотрим пример.

– 777 делится на 111? (Да, т. к. 777 = 111 ・ 7.)

– 111 делится на 3? почему? (да, т. к. 111 = 3 ・ 37.)

777 делится на 3, т. к. 777 = 7 ・ 37 ・ 3 = 3 ・ (37 ・ 7).

IV. Работа по учебнику

1. С. 123 (работа по статье учебника).

– Прочитайте текст и приготовьтесь отвечать на вопросы.

2. С. 125, № 3.370.

– Какие числа называются натуральными?

– Что мы называем натуральным рядом чисел?

– Выпишите первые 40 чисел в порядке возрастания.

– Какие числа нужно подчеркнуть чёрным цветом? (2, 4, 6, 8…, 40.)

– На какое число они делятся? (На 2.)

– Какие числа нужно подчеркнуть красным цветом? (5, 10, 15, 20, 25, 30, 35, 40.)

– На какое число они делятся? (На 5.)

– Зелёным? (10, 20, 30, 40.)

– Какие числа подчёркнуты двумя цветами? тремя цветами? (10, 20, 30, 40.)

– На какие числа они делятся? (На 2, 5, 10.)

3. С. 125, № 3.375.

– Сколько машинок в наборе? (5.)

– Что нужно сделать, чтобы проверить возможное количество купленных машин? (Поделить на 5 общее количество.)

1) 35 : 5 = 7 (набор.) – могло.

2) 42 : 5 = 8 (ост. 2) – не могло.

3) 60 : 5 = 12 (набор.) – могло.

4. С. 125, № 3.376 (устно).

1) 60 : 10 = 6 р. за бул. – мог.

2) 7500 к. : 10 = 750 к. = 7 р. 50 к. за бул. – мог.

3) 80 р. 15 к. = 8015 к.

4) 8015 к. : 10 = 801 (ост. 5) – не мог.

V. Повторение изученного материала

1. С. 126, № 3.396.

а) наибольший – 34, наименьший – 1;

б) наименьшее – 34, наибольшего не существует;

в) 42 : 3, 42 : 14. Общее кратное 42.

2. С. 126, № 3.397 (работа в паре).

Ответ:

а) 10, 20, 40, 50

б) 20, 40, 60, 80

в) 20, 40

г) 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

VI. Работа над задачей

1. С. 127, № 3.402 (1) (работа в паре).

1‑й способ

– Что будем принимать за x?

– После дождя во сколько раз прибавилось воды?

– Что ещё известно из условия?

– Сколько воды осталось?

Составим уравнение:

9x - 72 = 54

9x = 54 + 72

9x = 126

x = 126 : 9

x = 14 (л) – воды было изначально в бочке.

2‑й способ

1) 54 + 72 = 126 (л) – стало в бочке после дождя.

2) 126 : 9 = 14 (л) – воды было в бочке изначально.

2. С. 127, № 3.402 (2) (работа в паре с последующей взаимопроверкой).

х + 42 = 268 : 4

х + 42 = 67

х = 25 (ц) – привёз первый самосвал.

VII. Самостоятельная работа

1. Объясните, почему на 12 делится произведение:

а) 12 ・ 47 б) 12 ・ 120

2. Запишите числа 24, 42, 36, 72, 75 в виде произведения и покажите, что:

а) 24 делится на 12, т. к. 24 = 12 ・ 2

б) 42 делится на 21, т. к. 42 = 21 ・ 2

в) 36 делится на 6, т. к. 36 = 6 ・ 6

г) 72 делится на 9, т. к. 72 = 9 ・ 8

д) 75 делится на 25, т. к. 75 = 25 ・ 3

3. Напишите 5 чисел, кратных числу: а) 2; б) 5; в) 20; г) 7.

а) кратные 2: 2, 4, 6, 8, 10;

б) кратные 5: 5, 10, 15, 20, 25;

в) кратные 20: 20, 40, 60, 80, 100;

г) кратные 7: 7, 14, 21, 28, 56.

VIII. Рефлексия

– Что нового вы узнали сегодня на уроке?

Домашнее задание

С. 128, № 3.416, 3.418, 3.420.