Разработка урока № 2 "Порядок действий в вычислениях" (5 класс, учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков и др.)

У р о к № 2. Порядок действий в вычислениях

Основная дидактическая цель урока: формировать умение составлять программу выполнения действий в выражениях со скобками и без скобок, продолжить работу над текстовыми задачами.

Х о д у р о к а

I. Организационный момент

II. Устный счёт

1. При вычитании каких натуральных чисел в ответе будет 18?

Приведите примеры (88 - 70; 119 - 101). Сколько таких пар можно найти? (Бесконечное множество.)

2. При умножении каких натуральных чисел получится 18?

Сколько таких пар существует? (Ответ: 1 ∙ 18, 2 ∙ 9, 3 ∙ 6, 6 ∙ 3, 9 ∙ 2, 18 ∙ 1.)

3. При делении каких натуральных чисел получится 18?

Сколько таких пар можно указать? (180 : 10, пар бесконечное множество.)

4. Сколько различных двузначных чисел можно составить при помощи цифр 1, 7, 0? (6.)

5. Десять участников конференции обменялись рукопожатиями, пожав руку каждому. Сколько рукопожатий было сделано?

– Что можно сказать про две последние задачи?

– Вспомните, мы решали комбинаторную задачу про визитные карточки. Сколько визитных карточек было передано из рук в руки десятью участниками конференции? (90.)

– Чем отличается эта задача?

(Показать учащимся, что, когда обмениваются визитными карточками два человека, то 2 визитные карточки переходят из рук в руки, а рукопожатие между двумя людьми только одно (!), т. е. рукопожатий в два раза меньше, чем визитных карточек.)

Поэтому: 10 ・ 9 : 2 = 45 рукопожатий.

III. Работа по теме урока

Изложение теоретического материала согласно учебнику: при разборе примера (можно взять для начала пример проще, чем в учебнике) соответственно чертится схема вычислений.

(68 - 15) ・ 4 = 212

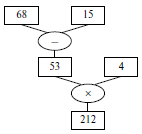
IV. Работа по учебнику

1. С. 109, № 3.268 (а–д).

– В каком порядке надо выполнять действия?

(33, 1400, 636, 4 793 236, 16 313.)

2. С. 110, № 3.272 (устно).

– Расскажите о порядке выполнения команд.

– Можно ли выполнить команды в другом порядке?

– Какой порядок выполнения команд удобнее? (Удобнее сначала выполнить команды в левой части схемы, а потом в правой.)

Ответ:

1) 690 : 23 = 30

2) 30 - 5 = 25

3) 3 ・ 26 = 78

4) 90 - 78 = 12

5) 25 ・ 12 = 300.

3. С. 110, № 3.274 (работа в паре).

(272, 23.)

V. Работа над задачей

С. 111, № 3.285.

– Сколько трёхлитровых банок?

– Сколько пятилитровых банок?

– Что сказано о вместимости всех банок?

– Что ещё известно в задаче?

– Прочитайте вопрос задачи.

– Что обозначим буквой х?

Пусть вместимость трёхлитровых банок х л. Тогда вместимость пятилитровых также х л.

В пятилитровых банках 5х л.

В трёхлитровых 3х л.

Во всех банках вместе (5х + 3х) л.

В условии сказано, что всего сока 120 л.

Значит, можем составить уравнение:

5х + 3х = 120

8х = 120

х = 120 : 8

х = 15 (л)

15 ・ 5 = 75 (л) – томатного сока.

VI. Работа в рабочей тетради

С. 34, № 2; с. 35, № 3.

– Каким будет порядок действий в каждом выражении?

VII. Рефлексия

– Внимательно посмотрите на плакат. Через 1 секунду плакат будет убран, а вы должны сложить три числа, которые были на нём, и назвать их сумму.

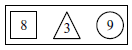
Эксперимент заключается в том, что дана установка: назвать сумму трёх чисел. А вопросы будут иметь другое содержание: какое число записано внутри квадрата, треугольника и круга.

Домашнее задание

С. 111, № 3.289; с. 112, № 3.292.