Геометрия 7 класс Дата: 03.12.2024
Урок № 25
Тема урока : «Свойства медианы прямоугольного треугольника, проведенной к гипотенузе»
Образовательная цель: Повторить свойства медианы в треугольнике , в прямоугольного треугольника, терему и доказательство, свойства и задачу из ЕГЭ.
Развивающая цель: развивать внимание, мышление учащихся;
развивать самостоятельность учащихся, используя проблемные ситуации, развивать познавательный интерес к предмету.
Воспитательная цель: воспитывать чувство взаимоуважения; воспитывать у учащихся навыки учебного труда.
Тип урока: Комбинированный
Метод. Словесный, беседа, рассказ
Литература : Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Оборудование: мел, доска, тряпка
ХОД УРОКА
Организационный момент . проверка посещаемости:
Проверка готовности к уроку.
Вступительное слово учителя. Сегодня мы продолжаем изучать свойства медианы в прямоугольном треугольнике.
Актуализация знаний учащихся. Фронтально-индивидуальный опрос по прямоугольному треугольнику 4-5 вопросов.
Дайте определение медианы.
Определение медианы треугольника
Возьми треугольник.
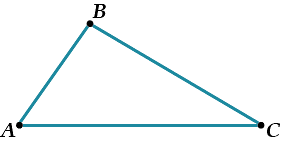
Отметь на какой-нибудь его стороне середину M.
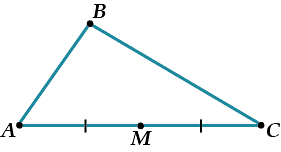
И соедини с противоположной вершиной.
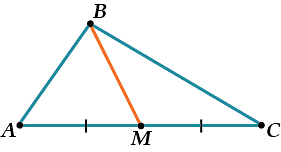
Получившийся отрезок BM и есть медиана. Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
2) Дайте формулировку теоремы о медиане в прямоугольном треугольнике.
Проведите доказательство теоремы методом от противного.

Перечислите свойства медианы в прямоугольном треугольнике.
Свойства медианы в прямоугольном треугольнике
Медианы в прямоугольном треугольнике пересекаются в одной точке, а точка пересечения делит их в соотношении два к одному считая от вершины, из которой проведена медиана.
Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.
Сформулируйте свойства медианы в произвольном треугольнике.
Теорема о трех медианах треугольника
Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1 , считая от вершины.
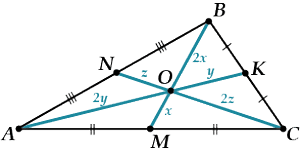
Посмотри на рисунок.
1. Медианы треугольника пересекаются в одной точке.
2. Точкой пересечения медианы делятся в отношении 2:1 , считая от вершины.
Мотивация учебной деятельности. Сообщение темы, цели, задачи урока.
Формирование умений и навыков на осмысление темы урока.
Теорема
Медиана прямоугольного треугольника
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Доказательство:
Пусть CM – медиана прямоугольного треугольника ABC с прямым углом C.
Продлим CM за точку M и отметим на луче CM точку K так, что CM=MK.
Треугольники BKM и ACM равны по углу и двум сторонам. Значит, углы BKM и ACM равны (накрест лежащие), тогда BK параллельна AC и BK=AC, AKBC – параллелограмм, причем угол C в нем – прямой.
Мы получили прямоугольник AKBC.
Диагонали прямоугольника равны и в точке пересечения делятся пополам.
Значит, CM=AM=BM= AB.
AB.
Задача ЕГЭ по теме «Медиана прямоугольного треугольника»
В треугольнике ABC угол ACB равен  угол B равен
угол B равен 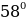 , CD – медиана. Найдите угол ACD. Ответ дайте в градусах.
, CD – медиана. Найдите угол ACD. Ответ дайте в градусах.
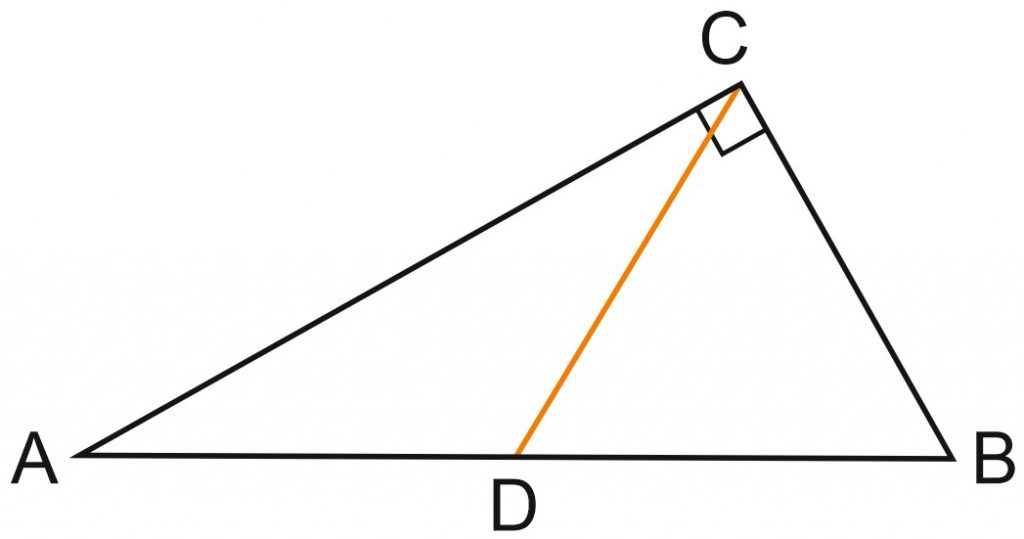
Решение:
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD – равнобедренный, CD=BD. Тогда
∠ DCB = ∠ DBC =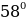 . Углы ACD и DCB в сумме дают
. Углы ACD и DCB в сумме дают  . Отсюда
. Отсюда
∠ACD = − ∠DCB =
− ∠DCB = −
−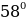 =
= .
.
Подведение итогов урока.
Домашнее задание:













 AB.
AB. угол B равен
угол B равен 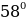 , CD – медиана. Найдите угол ACD. Ответ дайте в градусах.
, CD – медиана. Найдите угол ACD. Ответ дайте в градусах.
 . Отсюда
. Отсюда .
.









