Разработка урока

А(7) Дата 02.12.2024

Умножение степеней с одинаковыми показателями.

Для любых чисел a и b и любого натурального числа m выполняется равенство a^m ⋅ b^m = (ab)^m.

При перемножении степеней с одинаковыми показателями основания степеней перемножаются, а показатель степени остаётся тем же.

Данным правилом можно пользоваться как в одну, так и в другую сторону.

Это правило следует из того, что от перестановки множителей результат не меняется. Действительно,

Приведём примеры:

2⁷ ⋅ 5⁷ = (2 ⋅ 5)⁷ = 10⁷ = 10 000 000,

(5x)³ = 5³ ⋅ x³ = 125x³.

Рассматриваемое свойство справедливо и тогда, когда количество сомножителей в произведении, возводимом в степень, больше двух. Например,

Деление степеней с одинаковыми показателями.

Для любых чисел a и b = 0 и любого натурального числа m верно, что

a^m : b^m = (a : b)^m,

или, если записать в виде дроби,

При делении степеней с одинаковыми показателями основание степени делимого делится на основание степени делителя, а показатель степени остаётся тем же.

Данную формулу, как и все остальные правила работы со степенями, можно использовать как в одну, так и в другую сторону.

Доказательство этого свойства аналогично предыдущему доказательству. Действительно,

Освоение свойств степеней позволяет обратиться к такому полезному факту, как « Основной теоремой арифметики ».

Теорема. Каждое натуральное число n 1 можно представить в виде n = p₁ ⋅ ... ⋅ p_k, где p₁, ... , p_k — простые числа, причём такое представление единственно, если не учитывать порядок следования множителей.

Алгоритм разложения на простые множители понятный — нужно перебирать возможные простые делители и проверять, делится ли на них наше число. Можно также сначала разложить исходное число в произведение чисел поменьше, а затем раскладывать уже их. Например,

16 200 = 162 ⋅ 10 ⋅ 10 = (2 ⋅ 81) ⋅ (2 ⋅ 5) ⋅ (2 ⋅ 5) = (2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) ⋅ (2 ⋅ 5) ⋅ (2 ⋅ 5) =

= 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 5 = 2³ ⋅ 3⁴ ⋅ 5²

Разложение числа на простые множители можно переписать в каноническом виде. Для этого в разложении нужно объединить все одинаковые простые основания в соответствующую степень и упорядочить множители в порядке возрастания оснований (упорядочивают множители не всегда, но так удобнее). Тогда запись будет выглядеть так:

где p₁, ... , p_k — различные простые множители, входящие в разложение.

Например . 12 = 2² ⋅ 3 или 252 = 2² ⋅ 3² ⋅ 7.

При решении большого количества задач. Например, с её помощью удобно записывать правила для поиска наибольшего общего делителя и наименьшего общего кратного.

Закрепление : =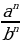

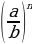
Упростить: 1. =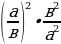

2. =

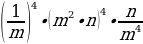3. =

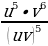4. Возвести в степень =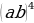

5. Найдите значение выражения : 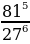=
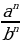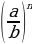
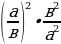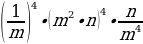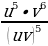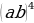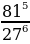