Раздел : Первообразная ,интеграл
Урок /2
Тема: Понятие первообразной F(x). Основное свойство первообразной. Решение упражнений
Образовательная цель: Сформировать понятие основного свойства первообразной F(x) + С ,доказательство и формулу; закрепить понятие первообразной, её обозначение, решить упражнения на нахождение первообразной функции в заданной точке.
Развивающая цель: развитие логического мышления, умение анализировать и выделять главное, активизация мыслительной деятельности.
Воспитательная цель: интерес к предмету, самостоятельность, точность и аккуратность математической записи.
Тип урока. Комбинированный.
Метод . Словесный, беседа, рассказ.
М/п связи: использование элементов интегрирования при вычислении в задачах по физике.
Литература /основная/. Алгебра и начала математического анализа .10-11 классы: учеб. для общеобразоват. организаций : базовый и углубл. Уровни/ ( Ш.А. Алимов и др.) ,-4-е изд.- М. : Просвещение, 2017.-463 с.
Дополнительная литература:
ТСО:
Дидактический материал:
Ход урока
1. Организационный момент
-приветствие классу;
-проверка готовности к уроку, проверка посещаемости;
-проверка выполнения Урок /1 домашнего задания. По Алимову №№ 983,984
2. Актуализация опорных базовых знаний. Вопросы с места. До 5 вопросов. Желательно их оценивать.
1) Приведите примеры прямых и обратных математических задач на основе дифференцирования и интегрирования функции.
Ответ. Если от заданной гладкой и непрерывной функции находят производную 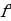 (x) , то нахождение производной или дифференцирование функции принимается в математике за «прямую математическую задачу». Существует обратное действие . Нахождение первообразной для заданной функции это обратная математическая задача.
(x) , то нахождение производной или дифференцирование функции принимается в математике за «прямую математическую задачу». Существует обратное действие . Нахождение первообразной для заданной функции это обратная математическая задача.
Физика . В разделе «Механика» пройденный путь S(t). Производная от пути по времени даёт значение скорости 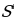 (t) = v(t). В данном случае это прямая математическая задача. Нахождение траектории движения материальной точки или пройденного пути по значению скорости является обратной математической задачей. Нахождение скорости движения материальной точки и её траектории движения по заданному значению ускорения а(t) тоже обратная математическая задача.
(t) = v(t). В данном случае это прямая математическая задача. Нахождение траектории движения материальной точки или пройденного пути по значению скорости является обратной математической задачей. Нахождение скорости движения материальной точки и её траектории движения по заданному значению ускорения а(t) тоже обратная математическая задача.
2) Как в математике называется операция нахождения первообразной от заданной функции?
Ответ. Операция нахождения первообразной от заданной функции f (x) называется – интегрированием данной функции f (x).
3) Используя таблицу первообразных, найти общий вид F(x) + С для функции:
а) f (x) = 2; Ответ: F(x) = 2х + С.
б) f (x) = - х; Ответ: F(x) = - 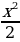 + С.
+ С.
4) Сформулируйте теорему, что называется первообразной
Ответ:
Теорема
Функция F(x) называется первообразной для функции f (x) на заданном промежутке, если для всех х из данного промежутка выполняется равенство: 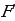 (x) = f (x).
(x) = f (x).
3. Мотивация учебной деятельности. Сообщение темы , цели и задачи урока. В процессе работы добавляем в таблицу первообразных новые функции и их первообразные:
| Функция f (x) | Первообразная F(x) + С |
| Число k | kx+ С |
| 5 | 5x+ С |
| x | 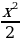 + C + C
|
| - х | - 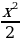 + C + C |
| 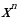
| 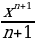 + C + C
|
| 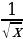
| 2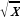 + С + С |
| 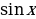
| - 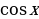 +С +С |
| 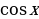
| 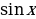 +С +С
|
4.Формирование новых знаний.
Если, 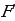 (x) = 0 на некотором промежутке l , то значение первообразной есть величина постоянная.
(x) = 0 на некотором промежутке l , то значение первообразной есть величина постоянная.
Задача нахождения первообразной не единственна, она имеет она имеет бесконечное число решений. Математически это записывается так, F(x) + С, где С- константа . ( « Constanta » в переводе с французского постоянная). Запись F(x) + С называется основным свойством первообразной функции и является самостоятельной формулой в интегрировании.
F(x) + С (1) Формула
Доказательство.
По условию F(x) является первообразной для функции f (x) на заданном промежутке l, тогда 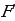 (x)= f (x), для любого х принадлежащих промежутке l,
(x)= f (x), для любого х принадлежащих промежутке l,
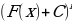 =
= 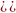 -
-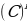 = f (x) + 0 = f (x).
= f (x) + 0 = f (x).
Геометрический смысл основного свойства первообразной состоит в том ,что графики любых первообразных для заданной функции получаются в результате параллельного переноса их вдоль оси ординат ОУ на постоянной значение константы С.
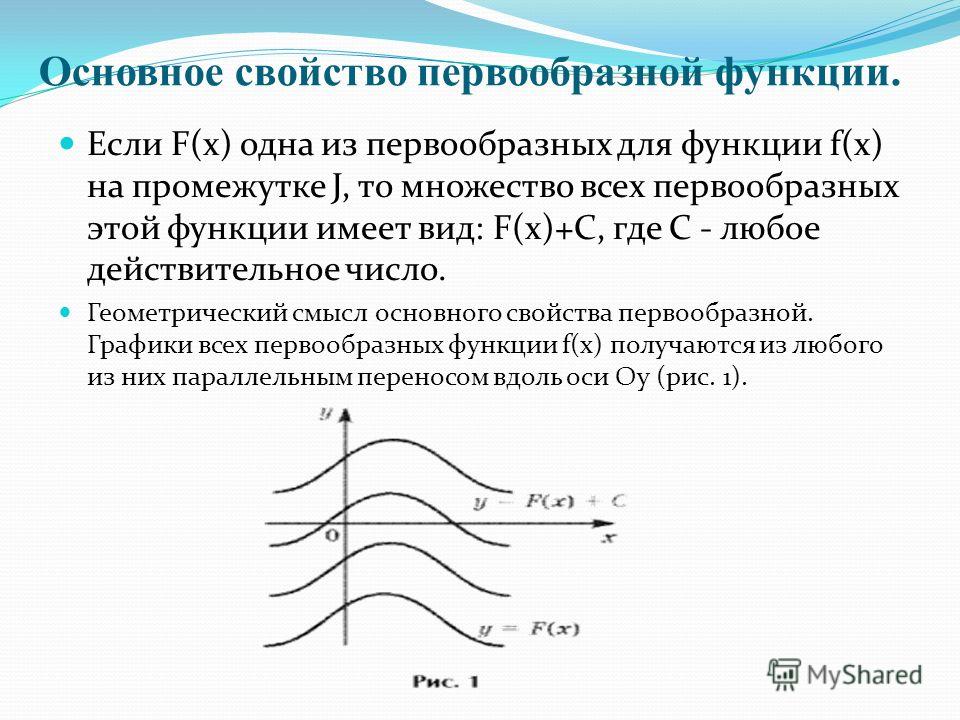
Закрепление:
Для функции f (x) =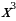 , найти первообразную график, которой проходит через точку М(2;1).
, найти первообразную график, которой проходит через точку М(2;1).
Решение: Общий вид первообразной для функции f (x) =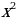 имеет вид
имеет вид
F(x) = 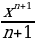 + C =
+ C = 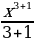 + C
+ C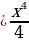 + C, в точке М (2;1)
+ C, в точке М (2;1)
1 = 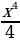 + C ; С = -3. Ответ: F(x) =
+ C ; С = -3. Ответ: F(x) =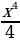 - 3.
- 3.
№ 986 2) стр . 293. Для функции 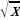 найти F(x) в точке М(9; 10). Выполнить самостоятельно.
найти F(x) в точке М(9; 10). Выполнить самостоятельно.
Домашнее задание: Алимов. стр 291-293, №№986 1). Выучить основное свойство первообразной. Пополнить таблицу и выучить её наизусть.







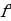 (x) , то нахождение производной или дифференцирование функции принимается в математике за «прямую математическую задачу». Существует обратное действие . Нахождение первообразной для заданной функции это обратная математическая задача.
(x) , то нахождение производной или дифференцирование функции принимается в математике за «прямую математическую задачу». Существует обратное действие . Нахождение первообразной для заданной функции это обратная математическая задача.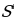 (t) = v(t). В данном случае это прямая математическая задача. Нахождение траектории движения материальной точки или пройденного пути по значению скорости является обратной математической задачей. Нахождение скорости движения материальной точки и её траектории движения по заданному значению ускорения а(t) тоже обратная математическая задача.
(t) = v(t). В данном случае это прямая математическая задача. Нахождение траектории движения материальной точки или пройденного пути по значению скорости является обратной математической задачей. Нахождение скорости движения материальной точки и её траектории движения по заданному значению ускорения а(t) тоже обратная математическая задача.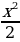 + С.
+ С.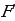 (x) = f (x).
(x) = f (x).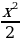 + C
+ C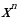
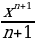 + C
+ C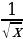
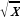 + С
+ С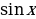
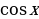 +С
+С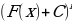 =
= 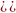 -
-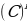 = f (x) + 0 = f (x).
= f (x) + 0 = f (x).
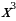 , найти первообразную график, которой проходит через точку М(2;1).
, найти первообразную график, которой проходит через точку М(2;1).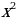 имеет вид
имеет вид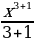 + C
+ C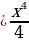 + C, в точке М (2;1)
+ C, в точке М (2;1)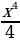 + C ; С = -3. Ответ: F(x) =
+ C ; С = -3. Ответ: F(x) =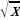 найти F(x) в точке М(9; 10). Выполнить самостоятельно.
найти F(x) в точке М(9; 10). Выполнить самостоятельно.









