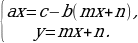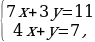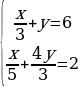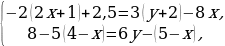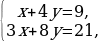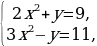ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
«АНТРАЦИТОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 3»
| РАССМОТРЕНО на ШМО учителей физико-математического цикла_ Протокол № от «_24_» февраля_ 2025 г. Руководитель ШМО Коленченко_И.В._/______/
|
|
|
Открытый урок по теме: «Решение систем линейных уравнений»
по предмету «алгебра»
7-Б класс (базовый уровень)
Составитель: Иоцук Марина Владимировна
учитель математики
категория высшая
Антрацит 2025
А (7 ) Дата: 24.02.2025
Урок № 67
Тема: «Решение систем линейных уравнений»
Образовательная цель: познакомить учащихся с новым методом решения систем линейных уравнений
Развивающая цель: развитие познавательного интереса к предмету; способствовать развитию творческой активности обучающихся; развивать логическое и образное мышление, способность рассуждать.
Воспитательная цель: формировать внимательность и точность в вычислениях; воспитывать чувство взаимопомощи.
Ключевые слова: уравнения, системы уравнений, решение, подстановка.
Тип урока: урок изучения нового материала. Соответствует обновлённому ФГОС
Формы организации работы: фронтальная, индивидуальная.
Ход урока.
«Предмет математики настолько серьезен,
что полезно не упустить случая сделать
его немного занимательным »
Блез Паскаль
1. Организационный момент.
2. Проверка домашнего задания.
Проверить наличие выполненных домашних заданий и ответить на вопросы, которые возникли у учеников во время их выполнения.
3. Сообщение нового материала.
В этом уроке мы рассмотрим новый метод решения систем линейных уравнений.
Использованный нами способ решения системы уравнений называется методом подстановки. Остаётся открытым вопрос: будет ли система, полученная методом подстановки, равносильна исходной? Ответ на этот вопрос положительный.
Докажем это с помощью основного утверждения о равносильности систем.
Если одно уравнение системы оставить без изменения, а вместо второго записать линейную комбинацию двух уравнений, то получится система, равносильная исходной.
Рассмотрим систему: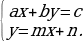
Здесь x и y — переменные, а a, b, c, m и n — числа.
Сначала посмотрим, какая система получится из исходной в результате подстановки в первое уравнение вместо переменной y выражения mx+n:
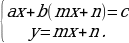 (2)
(2)
Теперь выполним равносильные преобразования исходной системы с помощью основного утверждения о равносильности систем. Вычтем из первого уравнения системы (1) второе, умноженное на b. Это приведёт нас к равносильной системе
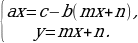
После переноса в первом уравнении слагаемого –b(mx+n) из правой части в левую с изменением знака (это равносильное преобразование) получим систему, равносильную исходной системе (1):
(3)

Осталось заметить, что система (2), полученная из исходной с помощью подстановки, и система (3), полученная из исходной с помощью основного утверждения о равносильности систем, совпадают.
Зафиксируем последовательность шагов при решении системы уравнений методом подстановки.
Алгоритм решения системы линейных уравнений методом подстановки
Выражаем из одного уравнения одну переменную через другую(можно также сказать, что мы решаем одно из уравнений относительно этой переменной).
Подставляем в другое уравнение системы вместо этой переменной найденное для неё выражение.
Решаем полученное уравнение с одной переменной.
Подставляя найденное из этого уравнения значение переменной в выражение для другой переменной, находим значение второй п
Самостоятельная работа
1.Решить систему линейных уравнений
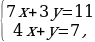
Какие из следующих преобразований системы являются равносильными?
В первое уравнение подставить выражение для x из второго уравнения, а во второе уравнение подставить выражение для x из первого уравнения.
В первое уравнение подставить выражение для x из второго уравнения, а второе уравнение заменить на сумму первого и второго уравнений.
В первое уравнение подставить выражение для x из второго уравнения, а второе уравнение оставить без изменений.
Закрепление учебного метериала.
1.Одно число в 2 раза больше другого. Если меньшее из этих чисел увеличить в 4 раза, а большее увеличить в 2 раза, то их сумма будет равна 44. Найдите эти числа.
Ответ : 5,5 ; 11.
2. На какие минимальные натуральные числа нужно домножить уравнения в системе, чтобы коэффициенты стали целыми?
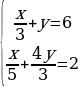
Ответ: на 3 и на 15.
3. Решить систему уравнений:
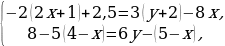
4.На пошив 1 платья и 4 юбок пошло 9 метров ткани, а на пошив 3 таких же платьев и 8 таких же юбок – 21 метр ткани. Сколько метров ткани нужно для пошива 1 такого платья и 1 юбки отдельно?
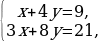
Ответ : На пошив юбки 1,5 метра, на платье -3 метра.
Решение заданий в формате ГИА
Решить систему уравнений
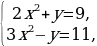
Ответ: (2; 1) ; ( - 2; 1) .
Домашнее задание: Сумма двух чисел равна 10, а их разность равна 4. Найти эти числа.
Анализ урока математики
Урок по теме: «Решение систем линейных уравнений» проведен в 7-Б классе учителем математики Иоцук Мариной Владимировной
Дата: 24 февраля 2025 г.
Урок алгебры проведен в 7 классе на тему: «Решение систем линейных уравнений».
Класс организован, но в дисциплине требует коррекции.
На уроке решались следующие задачи:
Образовательная цель: познакомить учащихся с новым методом решения систем линейных уравнений
Развивающая цель: развитие познавательного интереса к предмету; способствовать развитию творческой активности обучающихся; развивать логическое и образное мышление, способность рассуждать.
Воспитательная цель: формировать внимательность и точность в вычислениях; воспитывать чувство взаимопомощи.
Считаю, что логическая связь между различными этапами урока была выдержана: Составляющая теоретическая часть урока дана и алгоритм решения методом подстановки зафиксирован . Актуализация знаний фрагментарно подготавливала как текущее закрепление учебного материала, так и успешное выполнение самостоятельной работы.
Оборудование урока:
- учебник Алгебра 7 класс Ю. Н. Макарычева, рабочая тетрадь
- карточки для самостоятельной работы
Содержание урока
Соответствует учебной программе, поставленным задачам, способствовало формированию умения решать системы линейных уравнений. Содержание урока способствовало развитию аналитического мышления. Соответствует обновлённому ФГОС
Тип и структура урока:
Тип урока: Урок сообщения новых знаний
Для достижения целей весь материал был разделен на три блока:
Что знаем? Что хотим знать? Что узнали?
Знания подлежат прочному усвоению, их объем заложен в программе и они должны быть усвоены каждым учеником. Материал, близко примыкающий к основному, который расширяет и углубляет его и одновременно закладывает основу для дальнейшего изучения систем линейных уравнения рационализации решения текстовых задач.
Целостность знаний способствует общему развитию ученика.
В соответствии с поставленными целями и содержанием материала урок строился по следующим этапам:
Организационный момент.
Постановка учебной задачи.
Сообщение новых знаний.
Решение тренировочных упражнений.
Самостоятельная работа (с проверкой в классе) диагностического характера.
Итог урока.
Домашнее задание.
Все структурные элементы урока были выдержаны.
Целью первого этапа было быстро включить учащихся в деловой ритм, проверить готовность класса к уроку;
На третьем этапе были актуализированы теоретические знания, необходимые для работы над новым материалом и дан алгоритм решения систем уравнений . Одновременно шла эффективная работа над развитием речи, мыслительных операций, о чем свидетельствовала деятельность учащихся.
В процессе закрепления примеры решались с комментированием. При комментировании шла работа над речевой деятельностью, в которой они выражали суть выполняемых преобразований.
Решение тренировочных упражнений позволило закрепить новые знания и оценить степень усвоения материала.
Этап диагностической самостоятельной работы показал, что каждый ребенок смог себя проверить, осознать: все ли он понял, запомнил ли запись, решение . Считаю, что на данном этапе каждый ученик смог пережить ситуацию успеха.
На этапе итога урока обсудили условия рационального применения данного метода решения систем уравнений.
Реализация принципов обучения:
- принцип научности содержания учебного материала – содержание обучения знакомило учащихся с методологией решения систем уравнений и практическим применением систем линейных уравнений;
- принцип систематичности и последовательности в овладении нового материала – опора на прочно освоенные навыки решения систем уравнений;
- принцип доступности обучения заключался в том, что для учащихся для начала (в блоке актуализации знаний) предлагались несложные задания;
- принцип системности – связь материала с ранее усвоенным обеспечивает прочность знаний;
- принцип наглядности.
Методы обучения
Соответствовали задачам урока и по источнику передачи знаний были:
- словесные (рассказ, эвристическая беседа );
- наглядные (демонстрация );
- практические (составление и решение систем уравнений )
по уровню самостоятельности учащихся:
репродуктивные, проблемно – поисковые
по аспекту мышления:
продуктивные ( самостоятельное решение систем уравнений),
по логическому аспекту: - дедуктивные.
Общие результаты урока:
План урока выполнен, цели реализованы: учащиеся ознакомлены с методом подстановки при решении систем линейных уравнений для решения прикладных задач и задач ОГЭ.
Домашнее задание соответствует нормативным требованиям, содержит как новый материал, так и материал на повторение.
Недостатком проведения урока, считаю:
- отсутствие физкультминутки;
- учащиеся несколько «зажаты», «скованы» - эффект присутствия камеры;
- очень краткая инструкция по выполнению д/з.
Положительно оцениваю то, что:
- полностью удалось реализовать поставленные задачи; - каждый за урок получит оценку.







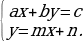
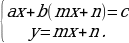 (2)
(2)