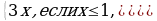А (7) Дата: 14.04. 2025
Тема урока: Свойства функций
Образовательная цель: в расширение и углубление представлений учащихся о свойствах функций в ходе выполнения упражнений; организация поисковой деятельности учащихся при определении свойств функции.
Развивающая цель: развитие логического мышления умения самостоятельно приобретать новые знания; использование для достижения поставленной задачи уже полученные знания; установление закономерности многообразия связей для достижения уровня системности знаний; способствовать выработке навыков и умений в построении графиков функций.
Воспитательная цель: в воспитание навыков самоконтроля, взаимоконтроля, ответственности, коллективизма, уважительного отношения к мнению одноклассников
Тип урока: Комбинированный
Метод. Словесный,беседа, рассках
Литература/основная/
Ход урока:
План урока:
Организационный момент
Индивидуальная работа и проверка домашнего задания .
Работа с задачником
Решение номера из дидактических материалов
Повторение ранее изученного материала
Подведение итогов урока
Дифференцированная проверочная работа
Домашнее задание
Организационный момент.
Приветствие
Проверка готовности к уроку- Откройте, пожалуйста, тетради, запишите сегодняшнее число и классную работу.
- Актуализация знаний по теме «Свойства функции», сегодня на уроке мы с вами повторим:
свойства функции;
правило нахождения области определения функции;
построение графика функции на заданном числовом промежутке;
нахождение наибольшего и наименьшего значения функции;
решение неравенства методом интервалов;
чтение графика функции;
решение квадратных неравенств;
извлечение квадратного корня;
как доказать возрастание и убывание функции;
нахождение координаты вершины параболы.
II. Индивидуальная работа и проверка домашнего задания.
Задания для карточек:
|
Карточка № 1 1. Докажите, что функция у = 4х – 9 возрастает. Какими свойствами вы руководствовались при выполнении данного задания? 2. Найдите наибольшее и наименьшее значения функции у = х2 + 3 на отрезке [0; 2].
|
Карточка № 2 1. Докажите, что функция у = -4х + 9 убывает. Какими свойствами вы руководствовались при выполнении данного задания? 2. Найдите наибольшее и наименьшее значения функции у = х4 – 5 на отрезке [0; 2]. |
Решения заданий по карточкам.
Карточка № 1.
1. у = 4х – 9 – линейная функция, т. к. k 0, сл – но: докажем, что она возрастает на всей числовой прямой.
0, сл – но: докажем, что она возрастает на всей числовой прямой.
Пусть х1 и х2 
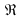 и выполняется неравенство х1 2. Тогда по свойствам числовых неравенств, будем иметь:
и выполняется неравенство х1 2. Тогда по свойствам числовых неравенств, будем иметь:
х1 2;
4х1 2;
4х1 – 9 2 – 9.
Последнее неравенство означает, что f(x1) f(x2), а это означает, что заданная функция возрастает (на всей числовой прямой).
2. Так как координата вершины параболы находится в точке (0; 3), сл – но; чтобы найти наибольшее и наименьшее значения функции на данном отрезке достаточно найти значения функции на концах данного отрезка.
если х = 0, то у = 02 + 3 = 0 + 3 = 3;
если х = 2, то у = 22 + 3 = 4 + 3 = 7.
унаим = 3; унаиб = 7.
Карточка № 2.
1. у = –4х – 9 – линейная функция, т. к. k 0, сл – но: докажем, что она убывает на всей числовой прямой.
0, сл – но: докажем, что она убывает на всей числовой прямой.
Пусть х1 и х2 
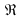 и выполняется неравенство х1 2. Тогда по свойствам числовых неравенств, будем иметь:
и выполняется неравенство х1 2. Тогда по свойствам числовых неравенств, будем иметь:
х1 2;
–4х1 –4х2;
–4х1 – 9 –4х2 – 9.
Последнее неравенство означает, что f(x1) f(x2), а это означает, что заданная функция убывает (на всей числовой прямой).
2. Так как координата вершины параболы находится в точке (0; –5), сл – но; чтобы найти наибольшее и наименьшее значения функции на данном отрезке достаточно найти значения функции на концах данного отрезка.
если х = 0, то у = 04 – 5 = 0 – 5 = –5;
если х = 2, то у = 24 – 5 = 16 – 5 = 11.
унаим = – 5; унаиб = 11.
В то время пока вы будите выполнять работы, с остальными мы устно сделаем задания, которые выписаны на доске. Тем самым проверю, как вы выполнили домашнее задание, потому что задания носят аналогичный характер; но сначала давайте вспомним схему описания свойств функции. (Учащиеся называют пункты схемы;
1. область определения;
2. промежутки возрастания или убывания;
3. ограниченность;
4. наибольшее или наименьшее значение;
5. непрерывность;
6. область значения;
7. выпуклость.
При необходимости повторить некоторые вопросы из следующего теоретического материала:
а) Что называется областью определения функции? (Если даны числовые множества Х и правило f, позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция у = f(х) с областью определения Х; пишут у = f(х), х  Х. При этом переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной, обозначается D(f).)
Х. При этом переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной, обозначается D(f).)
б) Что называется областью значения функции? (Множество всех значений
функции у = f(х), х  Х, называют областью значений функции и обозначают Е(f).)
Х, называют областью значений функции и обозначают Е(f).)
в) Какая функция называется возрастающей? (Функцию у = f(х) называют возрастающей на множестве Х  D(f), если для любых двух точек х1 и х2 множества Х, таких, что х1 х2, выполняется неравенство f(x1) f(x2).)
D(f), если для любых двух точек х1 и х2 множества Х, таких, что х1 х2, выполняется неравенство f(x1) f(x2).)
г) Какая функция называется убывающей? (Функцию у = f(х) называют убывающей на Х  D(f), если для любых двух точек х1 и х2 множества Х, таких, что х1 х2, выполняется неравенство f(x1) f(x2).)
D(f), если для любых двух точек х1 и х2 множества Х, таких, что х1 х2, выполняется неравенство f(x1) f(x2).)
Обобщение: функция возрастает, если большему значению аргумента соответствует большее значение функции; функция убывает, если большему значению аргумента соответствует меньшее значение функции.
д) Какая функция называется ограниченной снизу? (Функцию у = f(х) называют ограниченной снизу на множестве Х  D(f), если все значения функции на множестве Х больше некоторого числа (иными словами, если существует число т такое, что для любого значения х
D(f), если все значения функции на множестве Х больше некоторого числа (иными словами, если существует число т такое, что для любого значения х  Х выполняется неравенство f(x) m).)
Х выполняется неравенство f(x) m).)
е) Какая функция называется ограниченной сверху? (Функцию у = f(х) называют ограниченной сверху на множестве Х  D(f), если все значения функции меньше некоторого числа (иными словами, если существует число т такое, что для любого значения х
D(f), если все значения функции меньше некоторого числа (иными словами, если существует число т такое, что для любого значения х  Х выполняется неравенство f(x) m).)
Х выполняется неравенство f(x) m).)
ж) Что называется наименьшим значением функции? (Число т называют наименьшим значением функции у = f(х) на множестве Х  D(f), если:
D(f), если:
1) в Х существует такая точка х0, что f(х0) = т;
2) для всех х  Х выполняется неравенство f(х)
Х выполняется неравенство f(х)  f(х0).)
f(х0).)
з) Что называется наибольшим значением функции? (Число т называют наибольшим значением функции у = f(х) на множестве Х  D(f), если:
D(f), если:
1) в Х существует такая точка х0, что f(х0) = т;
2) для всех х  Х выполняется неравенство f(х)
Х выполняется неравенство f(х)  f(х0).)
f(х0).)
Вывод:
Если у функции существует унаим, то она ограничена снизу.
Если у функции существует унаиб, то она ограничена сверху.
Если функция не ограничена сверху, то унаиб не существует.
Если функция не ограничена снизу, то унаим не существует.
1. Прочитайте графики функций:
2. Найдите наибольшее и наименьшее значения функции:
а) у = 5х – 8, х  [0; 3].
[0; 3].
3. Используя свойства числовых неравенств, докажите, что данная функция возрастает:
у = 2х – 3.
4. Используя свойства числовых неравенств, докажите, что данная функция убывает:
у = – 3,5х + 5.
III.Работа с задачником
Откройте задачник на странице 67 № 259 (г),
г) у = -2х + 5, 0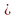 х
х 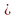 5
5
Для того, что бы ответить на поставленные вопросы мы должны построить график функции на данном отрезке.
Так как ,
у = -2х + 5 – линейная функция и ее графиком является прямая, то достаточно найти координаты двух точек и по ним построить прямую. В данном случае при подстановке вместо х будем использовать точки начала и конца отрезка.
если х = 0, то у = - 2 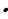 0 + 5 = 5,
0 + 5 = 5,
если х = 3, то у = - 2 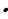 3 + 5 = 1.
3 + 5 = 1.
В прямоугольной системе координат строим график функции на заданном отрезке. Данная функция является ограниченной, так как она задана на отрезке.
Разбор решения № 267 (б).
б) у = х4 + 3х, х 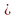 0
0
Для того что бы доказать, что функция возрастает на луче, нужно исследовать ее на монотонность на этом луче. Возьмем произвольные значения аргумента х1 и х2 и пусть х1 х2 принадлежат числовому множеству х 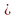 0. Тогда по свойствам числовых неравенств, будем иметь:
0. Тогда по свойствам числовых неравенств, будем иметь:
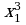
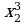 ;
;
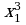 + 3
+ 3 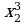 + 3;
+ 3;
х1(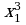 + 3) х2 (
+ 3) х2 (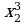 + 3).
+ 3).
Последнее неравенство означает, что f(x1) f(x2).
Итак, из х1 х2 следует f(x1) f(x2), а это означает, что заданная функция возрастает на данном числовом луче.
IV. Решение номера из дидактических материалов.
Постройте и прочитайте график функции у = f(х),
где f(x) =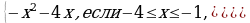
Решение.
Данная функция кусочная, значит, что бы построить ее график необходимо рассмотреть каждую из ее частей в отдельности, а затем построить в одной системе координат составляющие ее части и прочитать получившийся график. Для начала разобьем данную функцию на две и рассмотрим каждую из частей отдельно.
у1 = - х2 – 4х, если – 4 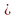 х
х  -1.
-1.
у1 = - х2 – 4х – квадратичная функция, графиком является парабола ветви
которой направлены вниз.
Так как отрезок, на котором надо построить график данной функции, невелик, следовательно: выполняем построение по точкам.
если х = - 4, то у = - (-4)2 – 4* (-4) = -16 + 16 = 0,
если х = - 3, то у = - (-3)2 – 4*(-3) = - 9 + 12 = 3,
если х = - 2, то у = - (-2)2 – 4*(-2) = - 4 + 8 = 4,
если х = - 1, то у = - (-1)2 – 4*(-1) = - 1 + 4 = 3.
у2 = 2, если х -1.
у2 = 2 – линейная функция, графиком является прямая, проходящая через точку (0; 2) и параллельная оси абсцисс.
В одной системе координат построим графики данных функций, на заданных множествах.
Свойства функции у = f(х):
D(f) = [-4; +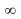 );
);
возрастает на отрезке [-4; -2];
убывает на отрезке [-2; -1];
постоянна на (-1; +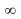 );
);
ограничена и снизу и сверху;
унаим = 0; унаиб = 4;
непрерывна;
Е(f) = [0; 4];
выпуклая вверх.
V.Закрепление ранее изученного материала
Найдите область определения функции: 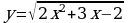 .
.
Решение.
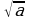 - имеет смысл, когда
- имеет смысл, когда 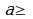 0, следовательно, имеем:
0, следовательно, имеем:
2х2 + 3х - 2 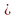 0.
0.
Введем функцию: у1 = 2х2 + 3х - 2.
Найдем нули функции, т. е. у = 0.
2х2 + 3х - 2 = 0, D = b2 – 4ac, D = 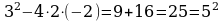
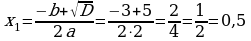 ;
; 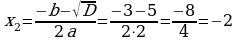
Решим неравенство методом интервалов:
если х = - 4, то у = 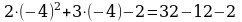 0;
0;
если х = 0, то у = 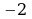 0;
0;
если х = 1, то у = 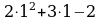
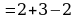 0.
0.
2х2 + 3х - 2 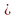 0, если х
0, если х  (-
(-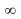 ; -2]
; -2] [0,5; +
[0,5; +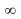 ) отсюда следует, что
) отсюда следует, что
D(y)  (-
(-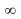 ; -2]
; -2] [0,5; +
[0,5; +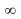 ).
).
Ответ: (-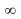 ; -2]
; -2] [0,5; +
[0,5; +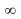 ).
).
Правильно. Убирай с доски и садись на место.
VI. Подведение итогов урока
1) Перечислите способы задания функции и охарактеризуйте их.
Ответ: аналитический – задание функции одной или несколькими формулами;
графический – задание функции с помощью графика;
табличный – задание функции с помощью таблицы, в которой даны значения аргумента и соответствующие им значения функции;
словесный – задание функции описывается словами.
Назвать свойства функции.
Перечислите свойства функции?
Ответ:
1. область определения;
2. промежутки возрастания или убывания;
3. ограниченность;
4. наибольшее или наименьшее значение;
5. непрерывность;
6. область значения;
7. выпуклость;
3) Выставление оценок за работу на уроке.
VIII. Домашнее задание (т. к. это последний урок по изучению темы, то домашнее задание записать в начале урока): решить из домашней контрольной работы № 3 на с. 84-85 № 1, № 4 на два варианта на отдельных листочках; к этим заданиям добавить еще № 271 (б, в) и № 272 (б, г)
VII. Дифференцированная проверочная работа
Вариант – 1
Постройте и прочитайте график функции у = f(x),
где f(x) = 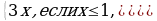
Вариант – 2
Используя свойства числовых неравенств, докажите, что функция у = 2,6х – 7 возрастает.
Найдите наибольшее и наименьшее значения функции
у = х2 – 4 на отрезке [1; 4].
Вариант – 3
1. Для данной функции ответьте на вопрос, является ли она ограниченной снизу, ограниченной сверху, ограниченной, использую график функции: у = – 3х + 1, х
2. Найдите наименьшее значение функции у = х2 – 8х + 2.
Вариант – 4
Используя свойства числовых неравенств, докажите, что функция у = – 3,4х – 5 убывает.
Найдите наибольшее и наименьшее значения функции
у = х2 + 5 на отрезке [-1; 4].
Вариант – 5
1. Используя свойства числовых неравенств, докажите, что функция
у = – 3,4х убывает.
Найдите наибольшее значение функции
у = 2х + 3 на луче (–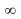 ; 3].
; 3].
Вариант – 6
1. Используя свойства числовых неравенств, докажите, что функция
у = 5х возрастает.
Найдите наибольшее значение функции
у = 2,5х – 4 на луче (–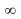 ; 2].
; 2].
Вариант – 7
Используя свойства числовых неравенств, докажите, что функция
у = – 4,5х убывает.
Найдите наименьшее значение функции
у = – 2х + 3 на луче (–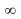 ; 0].
; 0].







 0, сл – но: докажем, что она возрастает на всей числовой прямой.
0, сл – но: докажем, что она возрастает на всей числовой прямой. и выполняется неравенство х1 2. Тогда по свойствам числовых неравенств, будем иметь:
и выполняется неравенство х1 2. Тогда по свойствам числовых неравенств, будем иметь: f(х0).)
f(х0).) 0 + 5 = 5,
0 + 5 = 5,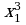
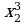 ;
;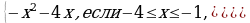
 );
);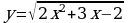 .
.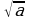 - имеет смысл, когда
- имеет смысл, когда 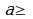 0, следовательно, имеем:
0, следовательно, имеем: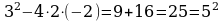
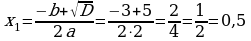 ;
; 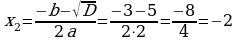
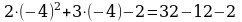 0;
0;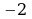 0;
0;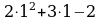
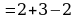 0.
0.