ТВиС (11) Дата: 22.09.2025
Урок № 4
Тема: Выборочный метод исследований
Перечень вопросов, рассматриваемых в теме:
Выборочный метод исследований — статистический метод, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой её части (выборке) на основе случайного отбора. Совокупность исследуемых объектов называется генеральной совокупностью, а часть объектов, подлежащих изучению, — выборочной совокупностью.
Необходимость выборочного метода может быть вызвана:
Обширностью объекта исследования — например, исследование потребительских предпочтений на рынке продукта, прогноз результатов голосования на выборах.
Необходимостью в сборе первичной информации в «пилотных» исследованиях.
Суть
Задача выборочного метода — дать верное представление о показателях всей генеральной совокупности на основе данных её части, попавшей в выборку. Это позволяет:
Сократить затраты на проведение наблюдения, так как отбирается только часть единиц.
Изучить явление более глубоко и детально — при сокращении объёма работы обследование можно провести по более широкой программе.
Виды
Некоторые виды выборочного метода:
Вероятностная выборка — каждый элемент генеральной совокупности имеет известную ненулевую вероятность попадания в выборку. Например, простая случайная выборка (каждый элемент совокупности имеет равную вероятность быть отобранным).
Систематическая выборка — отбор элементов через фиксированный интервал после случайного старта, например, каждый 10-й элемент из списка.
Стратифицированная (расслоённая) выборка — совокупность разделяется на непересекающиеся группы (страты), из каждой формируется отдельная выборка.
Кластерная выборка — совокупность разделяется на группы (кластеры), случайно отбираются несколько кластеров, внутри которых изучаются все элементы.
Правила формирования
Основная проблема — обеспечение репрезентативности — соответствия характеристик выборки характеристикам генеральной совокупности. Для этого необходимо соблюдать определённые правила, например:
Использовать основу выборки — полный список или перечень элементов генеральной совокупности.
Использовать объективные механизмы случайного отбора.
Минимизировать систематические ошибки при сборе данных.
Ошибки
Выборочные исследования всегда содержат неоднородные ошибки:
Случайные — ошибки, вызванные тем фактом, что исследуется не вся генеральная совокупность. Уменьшаются при увеличении размера выборки.
Систематические — ошибки, связанные с влиянием систематических факторов, которые приводят к смещениям оценок параметров, определяемых по выборке.
Некоторые преимущества выборочного метода по сравнению с другими методами:
Экономия ресурсов. Выборочный метод позволяет сократить объём работы, что снижает материальные, финансовые, трудовые и временные затраты на исследование.
Скорость получения результатов. Объём работы по сбору и обобщению результатов обследования меньше, поэтому результаты можно получить быстрее, чем при сплошном наблюдении.
Возможность детального изучения каждой единицы. Так как наблюдению подвергается лишь часть элементов общей совокупности, есть возможность расширить программу обследования и более широко изучить каждую единицу в отдельности.
Высокая достоверность получаемой информации. При относительно небольшом объёме выборки можно организовать эффективный контроль качества и снизить вероятность появления и необнаружения ошибок регистраци
Широкая область применения. Небольшой объём выборки позволяет использовать более сложные методы обследования, включая применение различных технических средств.
Использование в случаях, когда сплошное наблюдение невозможно. Например, в ситуациях, когда наблюдение связано с уничтожением или порчей обследуемых единиц (проверка качества продуктов питания).
Некоторые недостатки выборочного метода:
Ошибки репрезентативности. Они возникают из-за того, что наблюдаются не все единицы изучаемой совокупности. В результате выборочные данные не полностью совпадают с данными обработки генеральной совокупности.
Вероятность ложных результатов. Даже правильно составленная выборка может дать ложные результаты, если её объём слишком мал. С другой стороны, слишком большой объём выборки грозит исследователю огромными затратами.
Необходимость привлечения высококвалифицированного персонала. Это ведёт к увеличению стоимости обследования.
Трудности с определением объекта и единицы наблюдения. Это особенно сложно при изучении явлений, единицы которых отличаются высокой подвижностью.
Отсутствие единой научной терминологии. Это приводит к неоднозначным трактовкам
Актуализация базовых знаний
Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем значение x1 – наблюдалось n1 раз, x2 - n2 раз, ... xk - nk раз. n=n1+n2+...+nk – объем выборки.
Наблюдаемые значения называются вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом.
Числа наблюдений называются частотами (абсолютными частотами), а их отношения к объему выборки – относительными частотами или статистическими вероятностями.
Если количество вариант велико или выборка производится из непрерывной генеральной совокупности, то вариационный ряд составляется не по отдельным точечным значениям, а по интервалам значений генеральной совокупности. Такой вариационный ряд называется интервальным. Длины интервалов при этом должны быть равны.
Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (суммы частот, попавших в этот интервал значений).
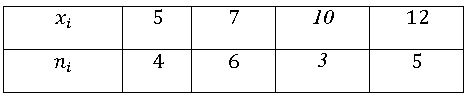
Точечный вариационный ряд частот может быть представлен таблицей:
| xi | x1 | x2 | ... | xk |
| ni | n1 | n2 | ... | nk |
Аналогично можно представить точечный вариационный ряд относительных частот.
Задача 1.
Число букв, соответствующих гласным звукам, в некотором тексте Х оказалось равным 1000. Первой встретилась буква «я», второй – буква «и», третьей – буква «а», четвертой – «ю». Затем шли буквы «о», «е», «у», «э», «ы».
Выпишем места, которые они занимают в алфавите, соответственно имеем: 33, 10, 1, 32, 16, 6, 21, 31, 29.
После упорядочения этих чисел по возрастанию получаем вариационный ряд: 1, 6, 10, 16, 21, 29, 31, 32, 33.
Частоты появления букв в тексте: «а» – 75, «е» –87, «и» – 75, «о» – 110, «у» – 25, «ы» – 8, «э» – 3, «ю» – 7, «я» – 22.
Составим точечный вариационный ряд частот:
| xi | 1 | 6 | 10 | 16 | 21 | 29 | 31 | 32 | 33 |
| ni | 75 | 87 | 75 | 110 | 25 | 18 | 3 | 7 | 22 |
Задача 2.
Задано распределение частот выборки объема n = 20.
Составьте точечный вариационный ряд относительных частот.
Решение.
Найдем относительные частоты:
| xi | 2 | 6 | 12 |
| wi | 0,15 | 0,5 | 0,35 |
При построении интервального распределения существуют правила выбора числа интервалов или величины каждого интервала. Критерием здесь служит оптимальное соотношение: при увеличении числа интервалов улучшается репрезентативность, но увеличивается объем данных и время на их обработку. Разность xmax−xmin между наибольшим и наименьшим значениями вариант называют размахом выборки.
Для подсчета числа интервалов k обычно применяют эмпирическую формулу Стреджесса (подразумевая округление до ближайшего удобного целого): k=1+3,322lgn.
Соответственно, величину каждого интервала h можно вычислить по формуле:
H=xmax−xmin1+3,322lgn
Эмпирическая функция распределения
Рассмотрим некоторую выборку из генеральной совокупности. Пусть известно статистическое распределение частот количественного признака Х. Введем обозначения: nx – число наблюдений, при которых наблюдалось значение признака, меньшее х; n – общее число наблюдений (объем выборки). Относительная частота события Х nxn. Если х изменяется, то изменяется и относительная частота, т.е. относительная частота nxn - есть функция от х. Т.к. она находится эмпирическим (опытным) путем, то она называется эмпирической.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию, определяющую для каждого х относительную частоту события Х
Различие между эмпирической и теоретической функциями распределения состоит в том, что теоретическая функция F(x) определяет вероятность события Х F∗(x) - относительную частоту этого же события. Для составления эмпирической функции распределения берется не вся генеральная совокупность, а выборка, и вероятность pi заменяется относительной частотой p∗i. При большом n F∗(x) и F(x) мало отличаются друг от друга.
Т.о. целесообразно использовать эмпирическую функцию распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.
F∗(x) обладает всеми свойствами F(x).
Значения F∗(x) принадлежат интервалу [0; 1].
F∗(x) - неубывающая функция.
Если x – наименьшая варианта, то F∗(x)=0, при хx1 ; если xk – наибольшая варианта, то F∗(x)=1, при хxk.
Т.е. F∗(x) служит для оценки F(x).
График эмпирической функции называется кумулятой.
Кумулята имеет такой же вид, как и график теоретической функции распределения.
Если задан интервальный вариационный ряд, то для составления эмпирической функции распределения находят середины интервалов и по ним получают эмпирическую функцию распределения аналогично точечному вариационному ряду.
Полигон и гистограмма
Для наглядности строят различные графики статистического распределения: полигон и гистограммы
Полигон частот - это ломаная, отрезки которой соединяют точки (x1;n1), (x2;n2),..., (xk;nk), где (xi) - варианты, (ni) – соответствующие им частоты.
Гистограмма частот -это ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны плотности частот.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-ый интервал. (Например, при измерении роста человека или веса, мы имеем дело с непрерывным признаком).
Пример:
Даны результаты изменения напряжения (в вольтах) в электросети. Составьте вариационный ряд, постройте полигон и гистограмму частот, если значения напряжения следующие: 227, 215, 230, 232, 223, 220, 228, 222, 221, 226, 226, 215, 218, 220, 216, 220, 225, 212, 217, 220.
Решение.
Составим вариационный ряд. Имеем n=20, xmin=212, xmax=232.
Применим формулу Стреджесса для подсчета числа интервалов.
k=1+3.322lg20≈5.
H=xmax−xmink=232−2125=4
Интервальный вариационный ряд частот имеет вид:
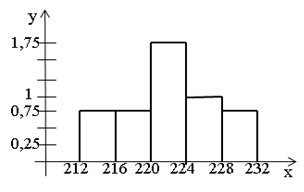
| интервалы | 212-216 | 216-220 | 220-224 | 224-228 | 228-232 |
| частоты | 3 | 3 | 7 | 4 | 3 |
| Относительные частоты (плотность частот) | 0,75 | 0,75 | 1,75 | 1 | 0,75 |
Построим гистограмму относительных частот
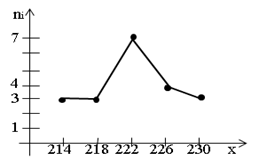
Построим полигон частот, найдя предварительно середины интервалов:
| Середины интервалов | 214 | 218 | 222 | 226 | 230 |
| частоты | 3 | 3 | 7 | 4 | 3 |
Задание:
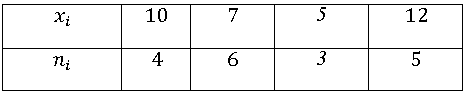
Пример точечного вариационного ряда может быть представлен таблицей: