Просмотр содержимого документа
«Разработка урока Алгебры 7 класс»
Разработка конспекта урока: Урок изучения нового
«Формула суммы и разности кубов»
Учитель математики МБОО «Черкехская СОШ имени П. А. Ойунского»: Легусина Розалия Егоровна
Учебник: 7 класс: учеб. для общеобразоват. учреж-дений/ авторы Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова [под редакцией С. А. Теляковского.] – 18-е изд. – М.: Просвещение, 2010. – 224 с. Глава IV «Разложение многочленов на множители», § 36 – Формула суммы и разности кубов.
Тип урока: урок изучения нового
Учебная задача: В совместной деятельности с учащимися вывести формулу суммы и разности кубов и выявить виды задач, решаемых на основе этой формулы
Диагностируемые цели:
В результате урока ученики:
- знают: словесную формулировку и символическую запись формулы суммы и разности кубов.
- умеют: формулировать правило разложения суммы и разности кубов на множители; применять формулы суммы и разности кубов для решения задач.
- понимают: для решения каких видов задач применяется формулы суммы и разности кубов.
Методы обучения: частично-поисковые, репродуктивный метод.
Форма работы: фронтальная.
Средства обучения: традиционные, презентация.
Структура урока:
Мотивационно - ориентировочный этап
Содержательный этап
Рефлексивно – оценочный этап
| Деятельность учителя | Деятельность учеников |
| Организационный этап (слайд 1) |
| Мотивационно – ориентировочный этап |
| Актуализация: Идёт фронтальная устная работа, учитель ведёт беседу с учениками. |
| Устный счет (слайд 2) |
| - Возведите в квадрат и куб: 2a -3 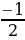 b b 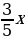 m4 | Решение: 4a2 8a3 9 - 27 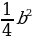 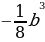   m8 m12 |
Используя формулу разности квадратов преобразуйте выражения (слайд 3): 1. (4-m)(4+m) 2. (с+0,2)(0,2-c) 3. (4с-3d)(4c+3d) 4. (7 -  ) ) 5. (a+b)(a-b) | Решение: 1) 16 – m2 2) 0,04 - c2 3) 16c2 – 9d2 4) 49 -  x2 x2 5) a2 – b2 |
| ПОВТОРЕНИЕ (слайд 4) Формула сокращенного выражения (a-b)(a-b)=a2-b2 Разность квадратов a2-b2=(a-b)(a-b) |
| Разность квадратов двух чисел равна произведению разности этих чисел и их суммы. a2 - b 2=(а+b)(a-b) Произведение разности двух чисел на их сумму равна разности квадратов этих чисел (а-b)(a+b)=a2 - b 2 |
| Мотивация (слайд 5): Прочитайте выражения и запишите 1. Разность чисел m и n 2. Разность квадратов чисел a и b 3. Квадрат суммы чисел a и b 4. Квадрат разности чисел a и b 5. Куб суммы чисел a и b 6. Куб разности чисел a и b 7. Сумма кубов чисел a и b 8. Разность кубов чисел a и b
Какие из этих формул вам известны, а какие мы еще не знаем. Как бы вы назвали формулы 5 и 6 |
1. m – n 2. a2 – b2 3. (a + b)2 4. (a - b)2 5. (a + b)3 6. (a - b)3 7. a3 + b3 8. a3 - b3
Формулы 5 и 6 называются
|
| Учебная задача урока: целью нашего урока будет: вывод формул суммы и разности кубов. |
| Деятельность учителя | Деятельность учеников |
| Содержательный этап |
| Работа в парах (слайд 6). Выполните умножение: 1. (a + b)(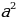 -ab+ -ab+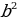 ) = ) = 2. (a -b)( ab+ ab+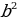 )= )= 1. а3 +b3 = (a+b)(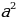 -ab+ -ab+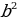 ) называют формулой суммой кубов двух чисел ) называют формулой суммой кубов двух чисел 2. a3- b3= (a -b)( ab+ ab+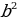 ) называют форму лой разности кубов двух чисел (слайд 7) ) называют форму лой разности кубов двух чисел (слайд 7) | 1. (a + b)(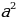 -ab+ -ab+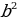 ) =a3 – ) =a3 –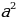 b+ ab2+ b+ ab2+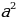 b- ab2 +b3 = a3+ b3 b- ab2 +b3 = a3+ b3 2. (a -b)( ab+ ab+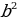 )=a3 + )=a3 +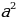 b+ ab2- b+ ab2-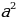 b- ab2 +b3= a3- b3 b- ab2 +b3= a3- b3
|
| Чем отличаются выражения (слайд 8) a2 + 2ab + b2 и a2 + ab + b2 a2 - 2ab + b2 и a2 - ab + b2
a2 + ab + b2 и a2 - ab + b2 называются неполными квадратами суммы и разности Формулы читаются: 1) Сумма кубов двух чисел равно произведению суммы этих чисел на неполный квадрат разности 2) Разность кубов двух чисел равно произведению разности этих чисел на неполный квадрат суммы
Т.к. с помощью этой формулы можно в дальнейшем быстро умножать сумму и разность двух чисел, то она относиться к формулам сокращённого умножения. | Первые формулы разложения полного квадрата суммы и разности. Во вторых формулах нет коэффициента 2 |
| Напишите неполный квадрат разности (слайд 9): a и b; c и d; Напишите неполный квадрат суммы: m и n; p и q; | 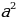 -ab+ -ab+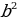 и и 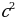 -cd+ -cd+
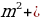 mn+ mn+ и и 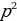 +pq+ +pq+
|
| Восстановите тождество (слайд 10): 1) 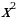 - … = ( ... - 2 - … = ( ... - 2 )( )(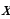 +…) +…) 2) …-n3 = (m - … )(… … … …) … … …) 3) … + 27y3 =(1 + …)(…-3y+…)  =… + 4х + … =… + 4х + …
|
1) 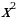 - 9y4 = (x. - 2 - 9y4 = (x. - 2 )( )(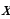 +2 +2 ) ) 2) m3-n3 = (m - n)(m2 mn+n2) mn+n2) 3) 1 + 27y3 =(1 + 3y)(1-3y+9y2) 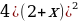 =4 + 4х + x2 =4 + 4х + x2
|
| Найдите ошибки, запишите верные тождества (слайд 11): 1) 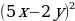 = 25 = 25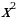 - 4 - 4 2) 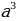 + 27b3 = (a-3b)( + 27b3 = (a-3b)(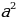 +6ab+9b2) +6ab+9b2)
|
1) 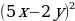 = 25 = 25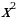 - 20xy+4 - 20xy+4 2) 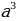 + 27b3 = (a+3b)( + 27b3 = (a+3b)( 6ab+9b2) 6ab+9b2)
|
| Работа по учебнику (слайд 12) Стр 170 Упражнения: № 905 (а, в д) № 906 (б, г, е
|
|
| Рефлексивно – оценочный этап |
| Самооценка (на листочках самооценки) (слайд 13) 1. Преобразование выражений (5) - …; 2. Запишите выражения (8) - …; 3. Неполный квадрат суммы и разности (4) - …; 4. Восстановите тождество (4) - …; 5. Найдите ошибку (2) - ; 6. Работа с учебником (6) - … | Всего – 29 баллов «5» - 27, 28, 29 баллов; «4» - 22 – 26 баллов; «3» - 17 – 21 баллов.
|
| Рефлексия (слайд 14) Что открыли, узнали на уроке? Какой этап урока был самый интересный? Какой этап урока был самый сложный? Определи своё настроение на уроке. |
|
| Каково ваше мнение от урока относительно этой китайской пословице (слайд 15): “Скажи мне – и я забуду, Покажи мне – и я запомню, Вовлеки меня – и я научусь” |
|
| - какова была цель урока?
- достигли ли мы её?
-как мы её достигли? Какие примеры решали на основе этой формулы?
| учится пользоваться формулой разности и суммы кубов для разложения многочлена на множители и решения других задач. - Да. Вывели формулы суммы и разности кубов с помощью умножения многочленов. -Решали задания и примеры, где нужно было разложить многочлен на множители, при этом пользовались формулами разности и суммы кубов. |
| Домашнее задание (слайд 16) Стр 170 Упражнения: № 905 (б, г, е) № 906 (а, в, д) ИЛИ Самим придумать примеры на применение Формул сокращенного умножения (ФСУ) |
|






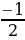 b
b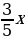
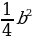
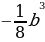


 )
) x2
x2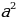 -ab+
-ab+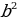 ) =
) = ab+
ab+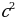 -cd+
-cd+
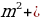 mn+
mn+ и
и 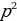 +pq+
+pq+
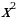 - … = ( ... - 2
- … = ( ... - 2 )(
)(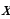 +…)
+…) … … …)
… … …) =… + 4х + …
=… + 4х + … 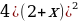 =4 + 4х + x2
=4 + 4х + x2 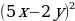 = 25
= 25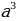 + 27b3 = (a-3b)(
+ 27b3 = (a-3b)( 6ab+9b2)
6ab+9b2)









