Разработка урока геометрии в 7 классе по теме «Медианы, биссектрисы, высоты треугольника»
Урок изучения нового материала
Цели урока:
-познакомить с понятиями «медианы, биссектрисы, высоты треугольника», сформировать умения грамотно выполнять алгоритмические предписания и инструкции при построении медианы, биссектрисы, высоты треугольника, научить
-научить распознавать в треугольнике медиану, биссектрису , высоту и применять эти понятия при решении задач;
Познавательные: формулирование проблемы, анализ объектов с целью выделения признаков, самостоятельное выделение- формулирование познавательной цели, проведение сравнений и классификаций по заданным критериям, закрепление, анализ, обобщение
Регулятивные: целеполагание, планирование, прогнозирование, контроль, оценка
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, договариваться и приходить к общему решению в совместной деятельности.
Ход урока
-
Организационный момент.
-
Актуализация опорных знаний.
Ребята, напомните мне, пожалуйста, о какой геометрической фигуре мы говорили с вами на прошлом уроке? (О треугольнике)
Сейчас, используя структуру МОДЕЛЬ ФРЕЙЕР (обучающая структура, помогающая учащимся понять и осознать изучаемые понятия и концепции.) запишите понятия, связанные с треугольником.
Как вы думаете это все известные людям понятия, связанные с треугольником? (Ответ учащихся)
Предположите, чем мы с вами сегодня будем заниматься на уроке? (Ответ учащихся)
Правильно, сегодня мы познакомимся с 3 замечательными отрезками, живущими в треугольнике. А как они называются, вы узнаете, разгадав ребусы. Вам знакомы эти понятия? Сформулируйте, пожалуйста, тему и цель урока. (Ученики записывают тему в тетрадь.)
В начале, прежде чем приступить к изучению темы, предлагаю вам выполнить небольшой тест по усвоению геометрических понятий. Вам предложены два- три варианта определения для каждого понятия. Вам необходимо выбрать верный и команда должна записать шифр, состоящий из номеров ответов. На выполнение задания Вам отводится 3 минуты .
Выполните вы этот тест с помощью структуры РАУНД ТЕЙБЛ. (обучающая структура, в которой учащиеся по очереди выполняют письменную работу по кругу на одном (на команду) листе бумаге.) (Проверка шифров.)
Выберите правильный ответ
-
Середина отрезка - это:
-
Точка, делящая отрезок на два отрезка.
-
Точка, делящая отрезок пополам, т.е. на два равных отрезка.
2) Биссектриса угла – это:
-
Отрезок, исходящий из начала угла и делящий его на два равных угла.
-
Прямая, делящая угол пополам.
-
Луч, исходящий из вершины угла и делящий его на два равных угла.
-
Перпендикуляр – это:
-
Отрезок АН , проведенный из точки А к прямой а, если прямые АН и а перпендикулярны.
-
Отрезок АН, проведенный из точки А к прямой a, если АН и a пересекаются.
-
Первый признак равенства треугольников:
-
Если две стороны одного треугольника равны двум сторонам другого треугольника, то такие треугольники равны.
-
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
-
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
-
Этап усвоения новых знаний.
Для того, чтоб выяснить что такое медиана, биссектриса, высота треугольника, предлагаю каждой группе выполнить практическую- исследовательскую работу, а кто-то может предположить, что такое медиана, высота, биссектриса треугольника
Н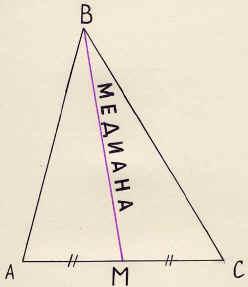 ачертите треугольник АВС и найдите середину стороны АС – точку М.
ачертите треугольник АВС и найдите середину стороны АС – точку М.
Что называется серединой отрезка? (Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка).
Запись на доске: АМ=МС.
Соедините точку М с вершиной В. Отрезок ВМ называется медианой треугольника.
Сможете дать определение данному понятию? Сравните его с определением в учебнике.
Определение. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Сколько вершин у треугольника? (3).
Сколько у него сторон? (3).
Как вы думаете, сколько медиан можно провести в треугольнике?(3).
-
“Проведите” три медианы треугольника.
-
Что вы заметили? Какое свойство медиан сможете сформулировать?
В любом треугольнике все медианы пересекаются в одной точке.
Эта точка называется центром тяжести треугольника.
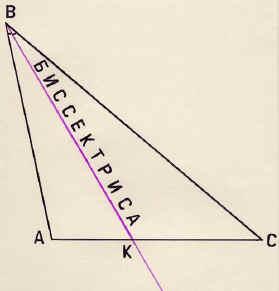
В начале урока мы повторили определение «биссектриса угла». Постройте биссектрису угла В треугольника АВС с помощью транспортира. Она пересечёт отрезок АС в точке К.
Отрезок ВК называется биссектрисой угла В треугольника АВС.
Ребята, сможете дать определение биссектрисы угла треугольника?
Определение. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.
Покажите все три биссектрисы на своем треугольнике.
Сформулируйте свойство биссектрис треугольника.
В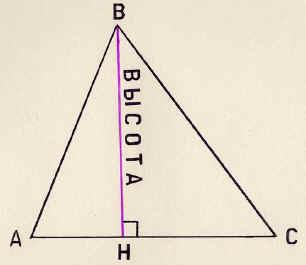 любом треугольнике биссектрисы пересекаются в одной точке.
любом треугольнике биссектрисы пересекаются в одной точке.
Дан треугольник АВС. С помощью чертёжного угольника из вершины В треугольника АВС проведём перпендикуляр ВН к стороне АС. Он называется высотой треугольника.
Сможете сформулировать самостоятельно определение?
Как вы думаете будут обладать высоты треугольника таким же свойством как медианы и биссетрисы?
Далее, учитель создает проблемную ситуацию.
Начертите треугольник АВС, у которого угол В – тупой. С помощью чертёжного угольника проведите его высоты.
Некоторые учащиеся будут испытывать затруднение при выполнении этого задания. Учитель предлагает выполнить это задание каждой группе с помощью структуры ФИНК-РАЙТ-РАУНД РОБИН («подумай-запиши-обсуди в команде». Во время выполнения данной структуры ученики ОБДУМЫВАЮТ задание или ответ на какой – либо вопрос, ЗАПИСЫВАЮТ и по очереди ОБСУЖДАЮТ свои ответы в команде).
После учитель проверяет решения учащиеся и показывает правильный вариант ответа.
Решение.
ВН1 АС, АН2
АС, АН2 ВС, СН3
ВС, СН3  АВ.
АВ.
Вывод. Высоты или их продолжения пересекаются в одной точке.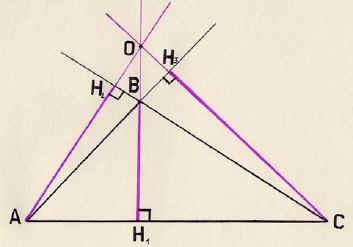
Эта точка называется ортоцентром.
Ребята, ваше ранее сформулированное определение было не точным. Сможете его исправить? Сравните его с определением в учебнике.
Определение. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.
-
Физкультминутка.
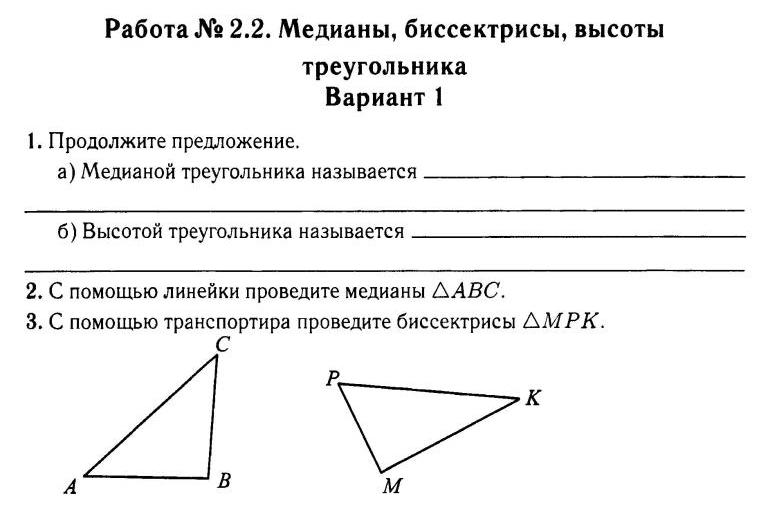
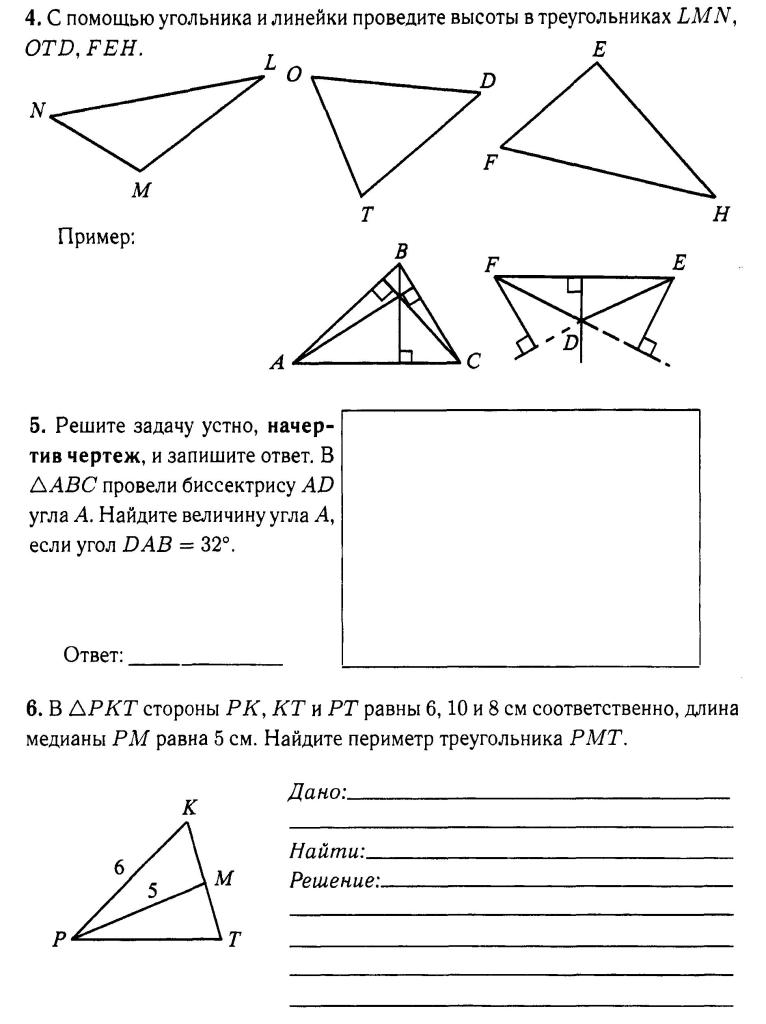
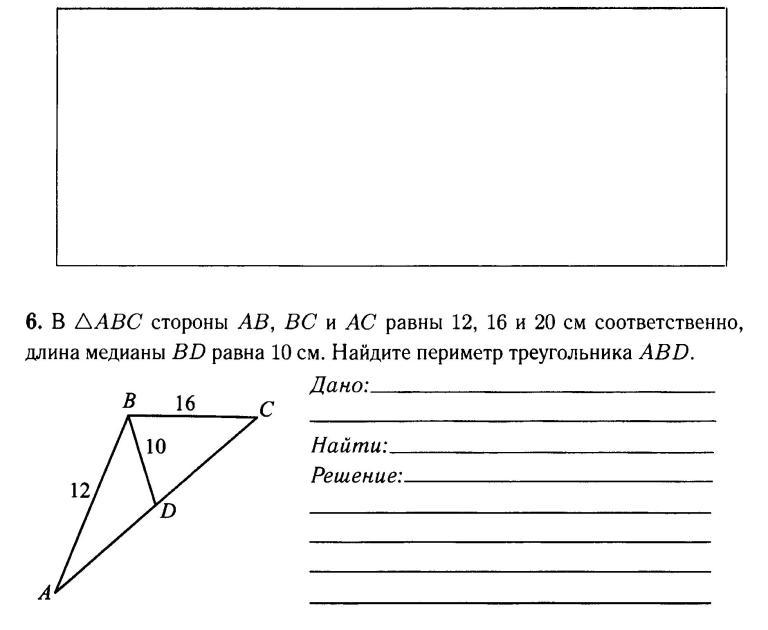
5) Первичное закрепление знаний. Найдите медианы, биссектрисы и высоты треугольников.
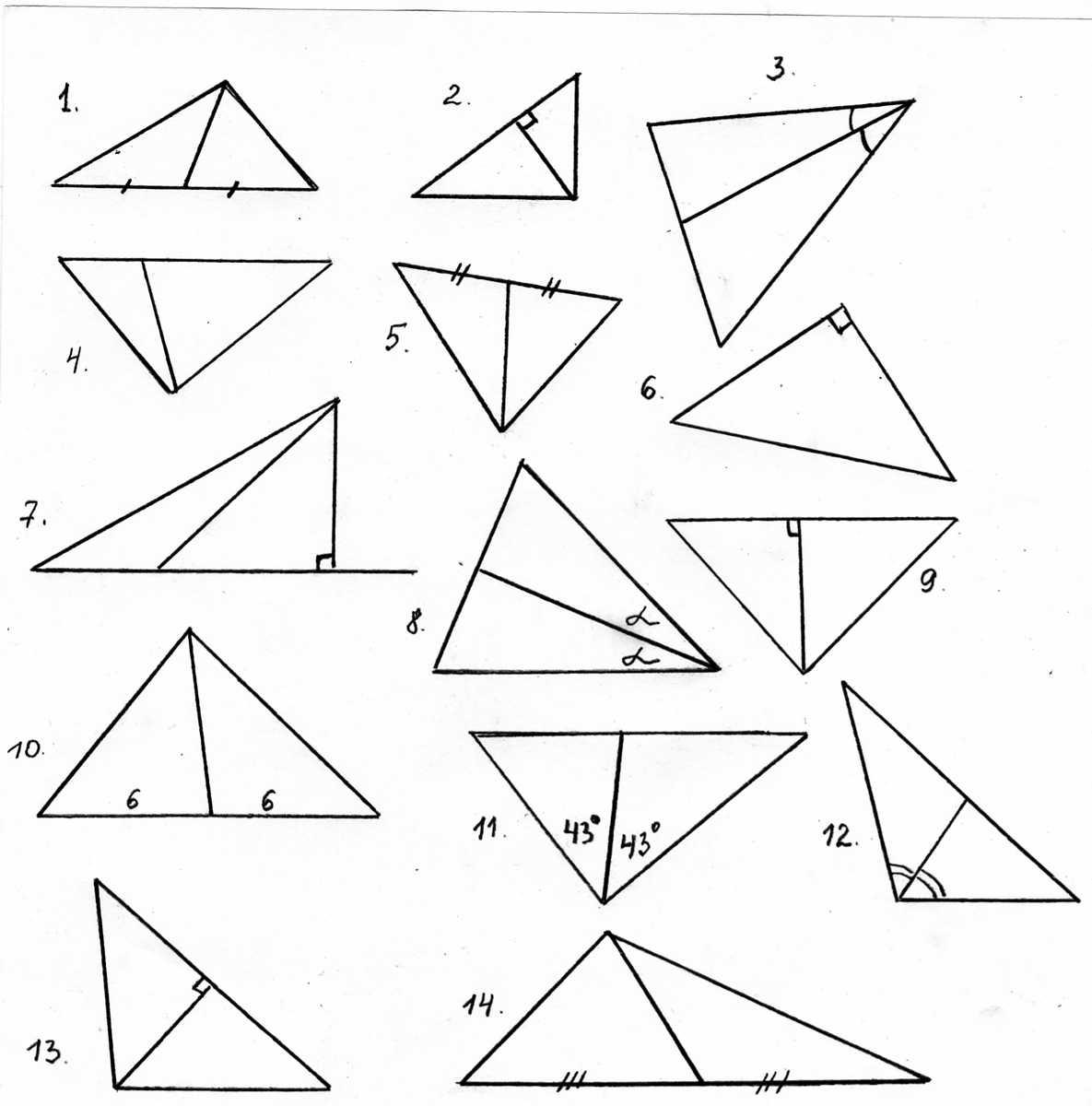
Д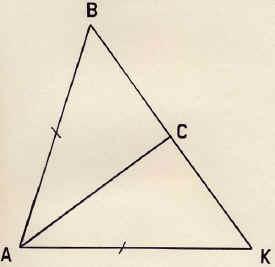 ано:
ано:  АВК
АВК
Доказать:  АВС=
АВС= АКС.
АКС.
Доказательство: АС – биссектриса угла А.
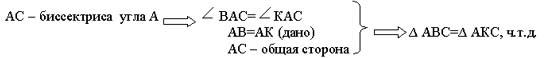
Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана треугольника».
На рисунке изображён треугольник ABC, при этом AD – медиана ∆ABC продолжена за сторону BC, так что AD = DE.
Докажем, что треугольники ABD и CED равны.
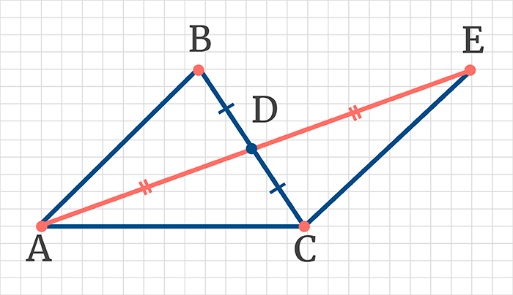
Дано:
АD – медиана ∆ABC.
AD = DE.
Доказать:
∆ABD = ∆CED.
Доказательство:
По условию в треугольниках ABD и CED: сторона AD равна стороне DE. Т. к. АD – медиана ∆ABC, то, по определению медианы, BD = DC.
∠ADB = ∠CDE (по свойству вертикальных углов).
Следовательно, ∆ABD = ∆CED (по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны).
Что и требовалось доказать.
Разбор решения заданий тренировочного модуля.
Задача 1.
В треугольнике ABC проведены биссектрисы AD и BM, которые пересекаются в точке O. Найдите углы треугольника ABO, если ∠BAC = 50°, ∠ABC = 80°, а сумма углов треугольника ABO равна 180°.
Р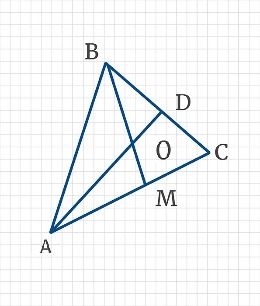 шение:
шение:
1.Нарисуем рисунок по условию задачи.
2.По условию AD и BM – биссектрисы ∆ABC.
∠BAC = 50°, ∠BAC = 2∠BAO =50° → ∠BAO = 25°
∠ABC = 80°, ∠ABC= 2∠ABO = 80°→∠ABO = 40°
3.Т. к. сумма углов треугольника ABO равна 180°, то ∠ABO + ∠BAO + ∠AOB = 180°.
4.25° + 40° + ∠AOB = 180°.
5.∠AOB = 180° – (25° + 40°) = 115°.
Ответ: ∠BAO = 25°, ∠ABO = 40°, ∠AOB = 115°.
Задача 2.
В треугольнике COD: ∠O = 90°. Найдите ∠МОВ, если ОА – биссектриса угла ∠СОM, при этом ∠COА = 20°, а ВО– биссектриса ∠МОD.
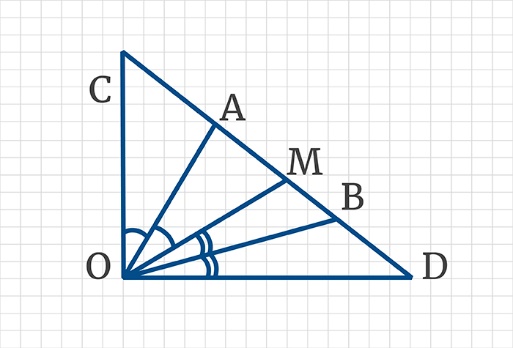
Решение:
1.По условию ∠СОD = 90°.
Кроме того, ОА – биссектриса угла ∠СОM → ∠МОА = ∠СОА = 20°.
2.ВО – биссектриса ∠МОD→∠ВОD = ∠МОВ.
3. ∠СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 20° + 20° + 2∠МОВ = 40° + 2∠МОВ = 90°.
4. 40° + 2∠МОВ = 90°.
∠МОВ = (90° – 40°):2 = 25°.
Ответ: ∠МОВ = 25°.
6.Рефлексия.
– Какая цель стояла перед вами?
- Достигли ли мы этой цели?
- Что нового узнали на уроке?
- Осталось ли что-то непонятным?
Далее ученики отвечают на вопросы, поднимая при этом столько пальцев руки, на сколько они сами себя оценили.
Как вы поняли новый материал урока?
Понравилось ли вам как прошел урок?
На сколько каждый из вас был активен на уроке?
7 . Домашнее задание. П.17, № 101,102,106. Выполнить творческую работу.






 ачертите треугольник АВС и найдите середину стороны АС – точку М.
ачертите треугольник АВС и найдите середину стороны АС – точку М.
 любом треугольнике биссектрисы пересекаются в одной точке.
любом треугольнике биссектрисы пересекаются в одной точке.

 ано:
ано: 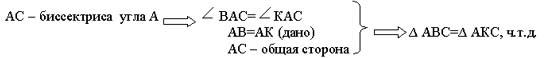

 шение:
шение:





















