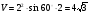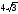| II. Постановка цели Сегодня на уроке мы повторим свойства объемов, следствие из теоремы об объеме прямоугольного параллелепипеда, какой многогранник называется призмой, какая призма называется прямой, какая призма называется правильной, изучим теорему об объеме прямой призмы, научимся решать задачи на вычисление объёма призм. | 1 | Сообщает дату проведения урока, тему урока, цель урока.
| Записывают в тетради.
|
| III Актуализация знаний. а)Какой многогранник называется призмой? (слайд презентации №2). б)Какая призма называется прямым? в)Какая призма называется правильной? г)Что является основанием правильной треугольной призмы? д) Чем являются боковые грани призмы? Прямой призмы? Правильной призмы? Выберите неверное утверждение: а)За единицу измерения объемов принимается куб, ребро которого равно единице измерения отрезков; б)тела, имеющие равные объемы, равны; в)объем прямоугольного параллелепипеда равен произведению трех его измерений; г)объем куба равен кубу его ребра; д)объем прямоугольного параллелепипеда равен произведению площади основания на высоту. (слайды презентации №3,4). е) Сформулируйте свойства объемов? Как вычислить объем прямоугольного параллелепипеда? Найдите объем прямоугольного параллелепипеда, если его длина равна 6 см, ширина — 7 см, а диагональ — 11 см.а) 252 см3; б) 126 см3; в) 164 см3; г) 462 см3; д) 294 см3.(слайд презентации №5). Решите устно: Измерения прямоугольного параллелепипеда равны 3 см, 18 см, 4 см. Найти ребро куба объем которого равен объему данного параллелепипеда (слайд презентации №6). Сформулируйте следствие из теоремы об объеме прямоугольного параллелепипеда, в основании которого прямоугольный треугольник. (слайд презентации № 7). | 5 | Проводит беседу.
Проверяет решение задач
| 1 ученик работают у доски по карточке, остальные принимают активное участие в устном опросе. Карточка №1 Решить задачу №653(д/з) Диагональ прямоугольного параллелепипеда равна 18 см и составляет угол в 30° с плоскостью боковой грани и угол в 45° с боковым ребром. Найдите объем параллелепипеда
|
| IV. Изучение нового материала. Докажем теорему. Объём прямой призмы равен произведению площади основания на высоту. (слайд № 8) Сначала докажем эту теорему для треугольной призмы, а затем – для произвольной.
Часть I (слайд № 9) Дано: ABCA1B1C1 – прямая призма. Доказать: V = Sосн ·h Доказательство. Проведем высоту BD┴АС, которая делит ∆АВС на два прямоугольных треугольника и плоскость (BDD1)┴ (ABC). Получим две призмы, основания которых прямоугольные треугольники, и они прямые, для вычисления объёма применим следствие 2
2) V1 и V2 их объемы V1 = SABD ·h, V2 = SDBC ·h, V= V1 + V2 = SABD ·h + SDBC ·h =h · (SABD+ SDBC) = h · SABC = Sосн ·h
II часть (слайд № 10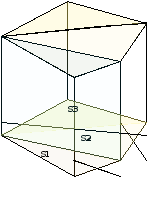 Рассмотрим n-угольную произвольную призму. Ее можно разбить на (n -2) прямые призмы (рис. 1). Объём каждой треугольной призмы можно вычислить, применяя I часть теоремы
V= V1+V2+ V3+…+ Vn-2 =S1 ·h +S2 ·h+S3 ·h+…+ Sn-2 ·h = = h · (S1 + S2 +S3 +…+Sn-2 )= = Sосн ·h
Т. о. V= Sосн ·h
рис. 1)
| 8
| Объясняет, используя презентацию. (слайды презентации №8, №9 и №10). |
Внимательно слушают объяснение учителя и записывают в тетрадь.
|
| V. Формирование умений и навыков учащихся
Решение задач по готовым чертежам (слайды презентации №11 и №12).
№1. В основании прямой призмы лежит прямоугольный равнобедренный треугольник АВС, ∠АСВ =90°, АС=СВ, точка N делит гипотенузу пополам. Отрезок С1N составляет угол 45° с плоскостью основания Боковое ребро равно 6 см/ Найти объём призмы.
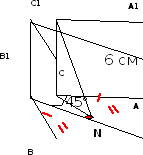
Дано: ABCA1B1C1- прямая призма, AC=BC, ∠АВС=90°, BN=NA, ∠CNC1= 45°, СС1=6 см. Найти: V 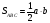 Решение. Решение. V= Sосн ·h, CN=CC1=6 cм, 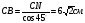
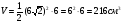
Ответ: 216 см3
№2. Основанием прямой призмы является ромб, острый угол которого 60°.Боковое ребро равно 2. Меньшая диагональ призмы составляет с плоскостью основания угол 45°. Найти объём призмы. Дано: ABCDA1B1C1D1- прямая призма, ABCD – ромб, ∠ВАD=60°, BB1=2, ∠B1DВ= 45°.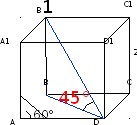 Найти: V 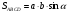 Решение. V= Sосн ·h Решение. V= Sосн ·h
∆ABD – равносторонний, AB=BD=2, т. к. ∆B1BD - равнобедренный 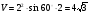
 Ответ:
VI. Самостоятельная работа
Решить задачу: Наибольшая диагональ правильной шестиугольной призмы равна 8 см и составляет с боковым ребром угол в 30°. Найти объём призмы. (слайд № 15) 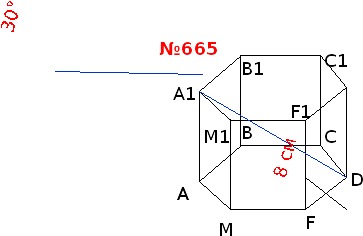
![]()
| 12
(6)
(6)
7
| Следит за верностью рассуждений учащихся. Демонстрирует на слайдах верное решение.
Задает наводящие вопросы: Что представляет собой правильная шестиугольная призма? (Слайд №13) Какая диагональ в этой призме является наибольшей? (Слайд №14) | Рассуждают устно, делая промежуточные записи в тетради.
Проверяют верно ли они решили задачи.
Самостоятельно решают задачу
Проверяют решение
|
| VII. Итог урока. Ответить на вопросы: а) Как вычисляется объем прямой призмы, основанием которой является прямоугольный треугольник? б) Как вычисляется объем правильной треугольной призмы? в) Как вычисляется объем правильной четырехугольной призмы? | 3 | Слайд № 16 Подводит итог урока, выставляет оценки.
|
Отвечают на вопросы
|
| IX. Домашнее задание. №659(а), №663(а, б), п.65 | 2 | Слайд № 18 Поясняет, какие формулы планиметрии понадобятся при выполнении домашнего задания | Внимательно прослушав пояснение учителя, записывают домашнее задание. |












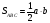 Решение.
Решение.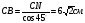
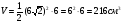

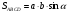 Решение. V= Sосн ·h
Решение. V= Sосн ·h