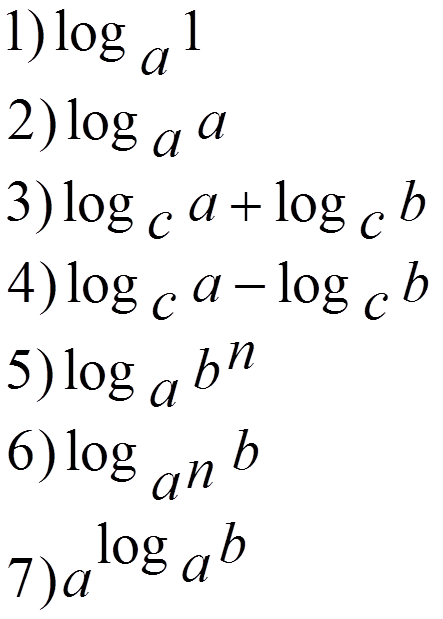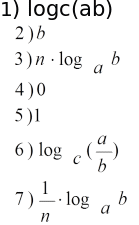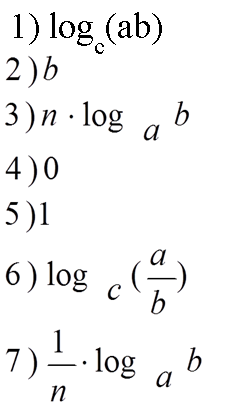МИНИСТЕРСТВО ОБРАЗОВАНИЯ КРАСНОЯРСКОГО КРАЯ
краевое государственное автономное профессиональное
образовательное учреждение
«Красноярский многопрофильный техникум имени В.П. Астафьева»
Урок по теме
«Логарифмические уравнения и методы их решения»
Преподаватель математики:
Федорова Елена Александровна
г.Красноярск 2023г.
Тема: Логарифмические уравнения и методы их решения
Цель: 1. Познакомить учащихся с методами решения логарифмических
2. Закрепить навыки решения логарифмических уравнений
Задачи:
Образовательные:
- повторить определение и свойства логарифмов;
- сформировать, обобщить и систематизировать знания и умения учащихся по применению методов решения логарифмических уравнений.
Развивающие:
- выработать умение мыслить, делать выводы, применять теоретические знания для решения задач;
- развивать самостоятельность, мышление, познавательный интерес.
Воспитательные:
- воспитание устойчивого интереса к математике;
- воспитание готовности и способности к самостоятельной творческой деятельности
- воспитаниецелеустремленности в поисках и принятии решений.
Тип занятия: изучение нового материала
Методы обучения: информационно-развивающий, наглядно-иллюстративный, проблемно-поисковый, групповой
Оборудование: интерактивная доска, компьютер, разноцветные фишки (красные, желтые, зеленые), магниты, карточки-задания для работы, индивидуальные карты, презентация.
План занятия:
I. Организационный момент
II. Создание проблемной ситуации. Подготовка учащихся к формулировке темы урока
III. Актуализация опорных знаний учащихся. Подготовка учащихся к активному и сознательному усвоению нового материала. Устная работа
IV. Изучение нового материала
V. Проверка понимания учащимися нового материала. Первичное закрепление материала
VII. Задание на дом. Подведение итогов
VIII. Рефлексия.
Ход занятия.
I. Организационный момент.

II. Создание проблемной ситуации. Подготовка учащихся к формулировке темы урока.
Учитель: Как вы успели заметить, на доске не записана тема сегодняшнего урока. Вам предстоит самим определить ее. Вы видите равенства, содержащие переменную (они заранее записаны на доске):
| log 4 (5𝑥 + 1) = −2 | log4(4x + 3) = log4 (x -11) | lg2x – 2lgx = 3 | lg(3x – 11) + lg(x – 27) = 3 |
Что общего у них?
Как называют эти равенства? ( Дается время на обдумывание).
Учащиеся отвечают: Эти равенства содержат переменную под знаком логарифма и называются логарифмическими. (Та группа, которая первая верно ответила на поставленные вопросы, с помощью магнита прикрепляет фишку своего цвета на доску.
Учитель: Итак, тема нашего урока «Логарифмические уравнения».
Сегодня на уроке мы повторим и обобщим наши знания о логарифмах и их свойствах, а также познакомимся с логарифмическими уравнениями и их решениями.
III. Актуализация опорных знаний учащихся. Подготовка учащихся к активному и сознательному усвоению нового материала. Устная работа
Учитель: Какие знания будут нам необходимы для решения логарифмических уравнений? (Каждому дается время на осмысление, после чего группы поочередно начинают выдвигать свои версии, причем каждый последующий ответ может быть лишь дополнением предыдущего).
Учащиеся отвечают: Чтобы решить логарифмические уравнения нужно знать:
1. Определение логарифма;
2. Формулы и свойства логарифмов;
3. Методы решения логарифмических уравнений.
(Все ответы преподаватель записывает на доске. Каждый верный ответ – фишка).
Учитель: И так давайте вспомним определение логарифма. Вам необходимо заполнить пропуски в предложении. Возьмите карточки № 1

Слайд 3
Учитель: Какие свойства логарифма мы можем использовать при решении логарифмических уравнений?
Чтобы ответить на этот вопрос, попытайтесь восстановить соответствие между элементами ряда 1 и ряда 2. (Возьмите карточки №2)
С лайд 4
лайд 4
(Каждое верное соответствие – фишка).
А теперь обменяйтесь карточками и проверьте, верно ли восстановлены соответствия. Но будьте внимательны, если вы исправите правильный ответ, то ваша команда лишится одного бала, а если найдете ошибку, то заработаете дополнительные баллы.
Учитель: Используя свойства и определение логарифма вычислите устно (задания проецируются на доску с помощью проектора).

Слайд 5
(Каждый верный устный ответ – фишка, причем выслушиваются версии каждой группы).
IV. Изучение нового материала.
Учитель: Молодцы. А теперь вернемся к теме нашего занятия. У вас на столе лежат карточки № 3 с уравнениями, вам необходимо распределить эти уравнения на группы (дается время на обдумывание).

Слайд 6.
Учитель:
1. Сколько групп выделили ?
2. Какие уравнения вошли в каждую группу.
3. Кратко прокомментируйте и аргументируйте по каким признакам были распределены уравнения.
Вспомните, какие методы решения уравнений вы знаете и какие из них можно применить для решения логарифмических уравнений. (Дается время на обдумывание, каждая группа записывает все возникшие идеи).
С лайд 7
лайд 7
Учащиеся называют методы решения, кратко комментируют сущность каждого и аргументируют возможность применения того или иного метода для решения логарифмических уравнений:
- по определению;
- метод потенцирования;
- преобразование уравнения по формулам;
- введение новой переменной;
Учитель: Замечательно. Но сегодня мы с вами остановимся только на некоторых из перечисленных вами методов.
С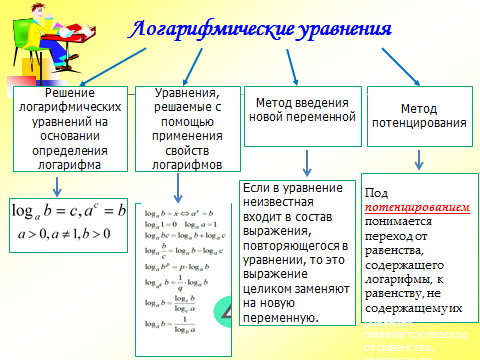 лайд 8
лайд 8
Каждый слайд комментируется преподавателем, а учащиеся фиксируют в своих тетрадях полученную информацию.
V. Проверка понимания учащимися нового материала. Первичное закрепление материала.
Учитель: Сейчас мы с вами просмотрели и записали информацию со слайдов.
Учитель: Как вы думаете, можно ли было бы как-то видоизменить первоначальную формулировку темы нашего занятия?
Учащиеся: Да, тема урока точнее будет звучать так: «Логарифмические уравнения и методы их решения».
Учитель: Совершенно верно.
С лайд 9
лайд 9
Учитель: Кто может сказать, что общего во всех методах и что необходимо знать, чтобы решить логарифмическое уравнение?
Учащиеся отвечают: (Учитель дописывает на доске)
1. Определение логарифма;
2. Формулы и свойства логарифмов;
3. Методы решения логарифмических уравнений;
4. Алгоритм решения
Учитель: Ребята, давайте попробуем составить алгоритм решения любого, независимо от вида и метода решения, логарифмического уравнения. На осмысление у вас есть 2 минуты.
Учащиеся отвечают:
Записать условия, задающие ОДЗ.
Выбрать метод решения.
Решить уравнение.
Проверить получившиеся корни, подставив их в условия ОДЗ.
При записи ответа исключить посторонние корни.
(Верный ответ – фишка).
С лайд 10
лайд 10
Учитель: А теперь давайте решим уравнения. (При выполнении решения уравнения каждое действие проговаривать).
VI. Домашняя работа
У вас на парте лежат карточки с домашним заданием, задания разноуровневые.
| I уровень на «3»: |
| а) 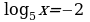 ; ; б) 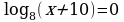 ; ; |
| II уровень на «4»: |
| а) 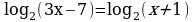 ; ; б) 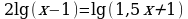 ; ; |
| III уровень на «5»: |
| а) 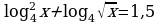 ; ; б) 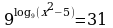 ; ; |
VII. Рефлексия.
Учитель: Давайте подведем итоги сегодняшнего занятия. Какие уравнения мы сегодня решали и какие знания нам помогали их решать?
Рефлексия. Выбрать смайлик, соответствующий настроению после урока.
| I уровень на «3»: |
| а) 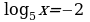 ; ; б) 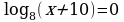 ; ; |
| II уровень на «4»: |
| а) 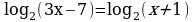 ; ; б) 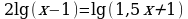 ; ; |
| III уровень на «5»: |
| а) 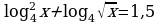 ; ; б) 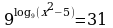 ; ; |
| I уровень на «3»: |
| а) 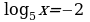 ; ; б) 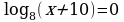 ; ; |
| II уровень на «4»: |
| а) 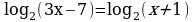 ; ; б) 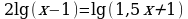 ; ; |
| III уровень на «5»: |
| а) 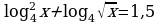 ; ; б) 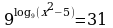 ; ; |
| I уровень на «3»: |
| а) 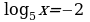 ; ; б) 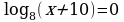 ; ; |
| II уровень на «4»: |
| а) 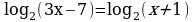 ; ; б) 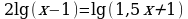 ; ; |
| III уровень на «5»: |
| а) 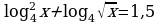 ; ; б) 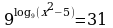 ; ; |
| I уровень на «3»: |
| а) 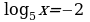 ; ; б) 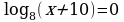 ; ; |
| II уровень на «4»: |
| а) 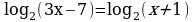 ; ; б) 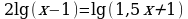 ; ; |
| III уровень на «5»: |
| а) 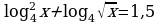 ; ; б) 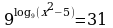 ; ; |
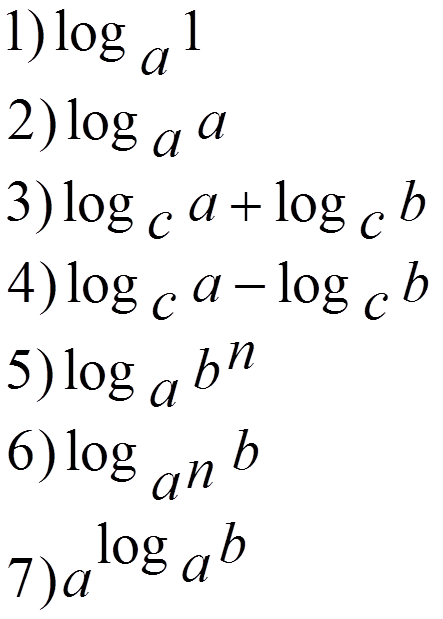

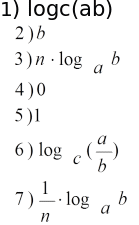
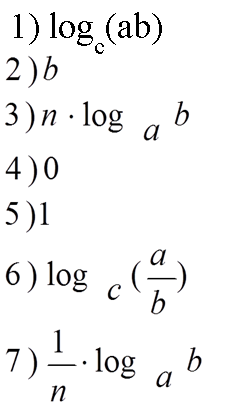
| 1. log3(1 – 2x) = 1 2. lg (x – 1) + lg (x + 1) = 3lg2 + lg (x – 2) 3. log3 (x – 12) = 2 4. log4(x + 3) – log4 (x – 1) = 2 – log4 8 5. log4(4x + 3) = log4 (x -11) 6. log2(5x + 3) – log2(3x – 1) = 2 7. log3(x2 – 5x + 7) = 1 8. log32x + log3x = 2 9. lg(x2 – 17) = lg(x +3) 10. lg(3x2 – 17x + 2) = lg(x2 – 6x + 1) 11. log32x – 3log3x – 10 = 0 12. 2log32x – 7log3x + 3 = 0
| 1. log3(1 – 2x) = 1 2. lg (x – 1) + lg (x + 1) = 3lg2 + lg (x – 2) 3. log3 (x – 12) = 2 4. log4(x + 3) – log4 (x – 1) = 2 – log4 8 5. log4(4x + 3) = log4 (x -11) 6. log2(5x + 3) – log2(3x – 1) = 2 7. log3(x2 – 5x + 7) = 1 8. log32x + log3x = 2 9. lg(x2 – 17) = lg(x +3) 10. lg(3x2 – 17x + 2) = lg(x2 – 6x + 1) 11. log32x – 3log3x – 10 = 0 12. 2log32x – 7log3x + 3 = 0
|
| 1. log3(1 – 2x) = 1 2. lg (x – 1) + lg (x + 1) = 3lg2 + lg (x – 2) 3. log3 (x – 12) = 2 4. log4(x + 3) – log4 (x – 1) = 2 – log4 8 5. log4(4x + 3) = log4 (x -11) 6. log2(5x + 3) – log2(3x – 1) = 2 7. log3(x2 – 5x + 7) = 1 8. log32x + log3x = 2 9. lg(x2 – 17) = lg(x +3) 10. lg(3x2 – 17x + 2) = lg(x2 – 6x + 1) 11. log32x – 3log3x – 10 = 0 12. 2log32x – 7log3x + 3 = 0
| 1. log3(1 – 2x) = 1 2. lg (x – 1) + lg (x + 1) = 3lg2 + lg (x – 2) 3. log3 (x – 12) = 2 4. log4(x + 3) – log4 (x – 1) = 2 – log4 8 5. log4(4x + 3) = log4 (x -11) 6. log2(5x + 3) – log2(3x – 1) = 2 7. log3(x2 – 5x + 7) = 1 8. log32x + log3x = 2 9. lg(x2 – 17) = lg(x +3) 10. lg(3x2 – 17x + 2) = lg(x2 – 6x + 1) 11. log32x – 3log3x – 10 = 0 12. 2log32x – 7log3x + 3 = 0
|
|
1. Логарифмом числа b по …………… а называется …………….. степени, в которую нужно……………. основание а, чтобы получить число b. 2. Основание и число, стоящее под знаком логарифма, должны быть…………. 3. Если основание а =….., то такой логарифм называется десятичным и обозначается lg b.
|
|
1. Логарифмом числа b по …………… а называется …………….. степени, в которую нужно……………. основание а, чтобы получить число b. 2. Основание и число, стоящее под знаком логарифма, должны быть…………. 3. Если основание а =….., то такой логарифм называется десятичным и обозначается lg b.
|
|
1. Логарифмом числа b по …………… а называется …………….. степени, в которую нужно……………. основание а, чтобы получить число b. 2. Основание и число, стоящее под знаком логарифма, должны быть…………. 3. Если основание а =….., то такой логарифм называется десятичным и обозначается lg b.
|
|
1. Логарифмом числа b по …………… а называется …………….. степени, в которую нужно……………. основание а, чтобы получить число b. 2. Основание и число, стоящее под знаком логарифма, должны быть…………. 3. Если основание а =….., то такой логарифм называется десятичным и обозначается lg b. |









 лайд 4
лайд 4

 лайд 7
лайд 7 лайд 8
лайд 8 лайд 9
лайд 9 лайд 10
лайд 10 ;
; ;
; ;
;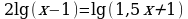 ;
;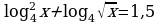 ;
;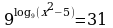 ;
;