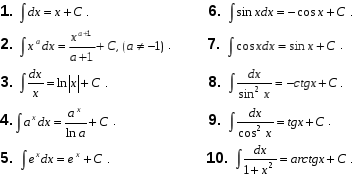Разработка урока по теме "Первообразная. Неопределенный интеграл".

Министерство образования и науки Республики Казахстан

Открытое занятие

по дисциплине «Математика»

на тему «Первообразная. Неопределенный интеграл, его свойства»

Разработал: преподаватель

Тасмагамбетова К.Ж.

Тақырыбы:

Тема: Первообразная. Неопределенный интеграл, его свойства.

Сабақтың мақсаты:

Цель занятия: ввести понятие первообразной, неопределенного интеграла, отработать навыки использования свойств неопределеного интеграла и таблицы интегралов.

Негізгі ұғымдар:

Основные понятия: первообразная, неопределенный интеграл, функция, подинтегральное выражение, интегрирование и т.д.

Сабақтың әдістемелік жағынан қамтамасыз етілуі:

Методическое обеспечение: А.Н. Колмогоров «Алгебра и начала анализ» 10-11 кл,

Сабақтың типі:

Тип занятия: комбинированный

Сабақтың әдіс-тәсілдері:

Методы и приемы: рассказ, беседа, конспект

Сабақ жоспары:

План занятия:

1. Ұйымдастыру кезеңі:

Организационный момент:

Приветствие, проверка присутствующих, проверка готовности аудитории к занятию, сообщение темы, цели и хода занятия.

2. Оқушылардың білімдерін тексеру:

Проверка знаний учащихся:

Сообщение оценок за самостоятельную работу по закреплению пройденного раздела «Производная и ее приложение».

3. Жаңа материалды оқыту:

Изучение нового материала:

Сегодня мы перейдем к изучению нового раздела «Первообразная и интеграл», которая непосредственно взаимосвязана с предыдущем разделом «Производная и ее приложение».

Известно, что каждому математическому действию соответствует обратное ему действие. На прошлых занятиях вы научились находить производные функций, т. е. дифференцировать функции. Для дифференцирования существует обратное действие – интегрирование: нахождение функции (восстановление функции) по заданной ее производной или дифференциалу. Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной.

Определение. Функция F(х) называется первообразной для функции f(х) на заданном промежутке, если для всех х из этого промежутка справедливо равенство F′(x)=f(x).

Примеры. 1)

Доказать что, функция F(x)=х³ первообразной для f(x)= 3x². По определению найдем производную от первообразной, (х³)′=3х².

Значит, функция F(x)=х³ – первообразная для функции f(x)= 3x².

Пример. 2)

(sin2x)′=2cos2x. Значит, первообразной для функции f(x)=2cos2x является функция F(x)=sin2x.

Дифференцирование функции – однозначная операция, т. е. если функция имеет производную, то только одну! Интегрирование, как и всякое обратное действие, неоднозначно! Смотрите сами: в первом примере функция F(x)=x³ являлась первообразной для функции f(x)=3x² потому что F′(x)=(x³)′=3x²=f(x).

Но ведь и (x³+4)′=3x², значит и функция F(x)=x³+4 будет первообразной для функции f(x)=3x², да и любая другая функция вида F(x)=х³+С будет служить первообразной для f(x)=3x², так как F′(x)=(x³+C)′=3x²=f(x).

Т.е всякая функция вида х³ + С, где С – некоторое число, является первообразной функции 3х².

Теорема. Если функция f(х) имеет на промежутке первообразную F(х), то для любого числа С функция F(х)+ C также является первообразной для f(х) . Иных первообразных функция f(х) на Х не имеет.

Доказательство

Т.к. F(х)- первообразная для f(х) на промежутке Х, то F(x)=f (x) для всех х Х. Тогда для х Х для любого С имеем : (F(x)+C)=f(x).Это значит, что F(x)+C – тоже первообразная f(х) на Х. ч.т.д.

Определение Совокупность всех первообразных F(x)+C функции f(x) на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом ∫f(x)dx,

Где

∫ - знак интеграла

f(x)-подынтегральная функция,

f(x)dx-подынтегральное выражение,

х-переменная интегрирования.

Пример 1) можно записать так: ∫3х²dx=x³+C.

Исходя из определений первообразной и неопределенного интеграла, рассмотрим основные формулы и свойства неопределенного интеграла.

Свойства неопределенного интеграла

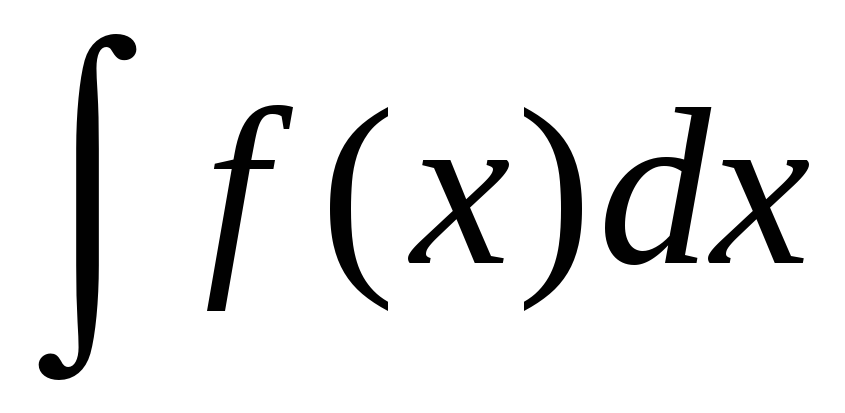1. ( )^’ = f (x) производная неопределенного интеграла равно подынтегральной функции.

2. Постоянный множитель можно вынести за знак интеграла.

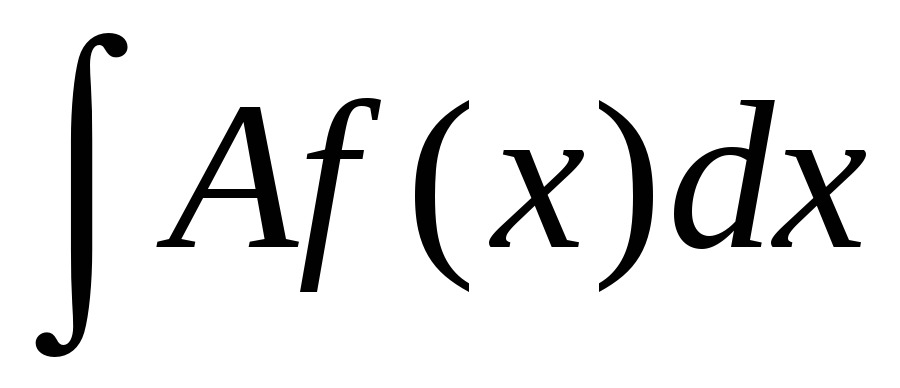= A .

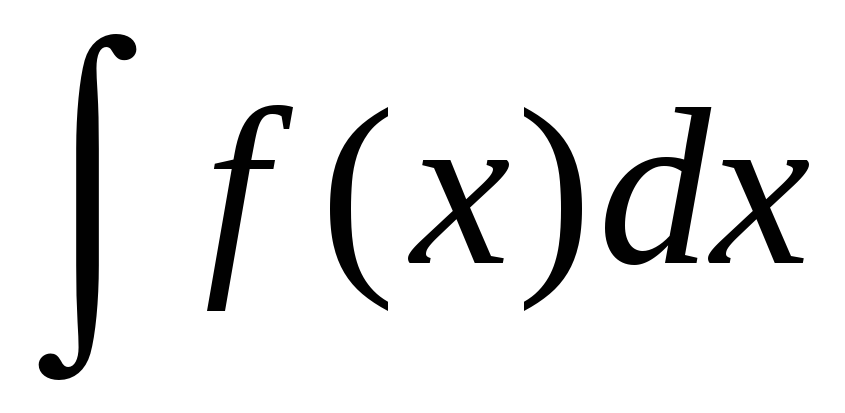1. Интеграл суммы равен сумме интегралов слагаемых.

= + .

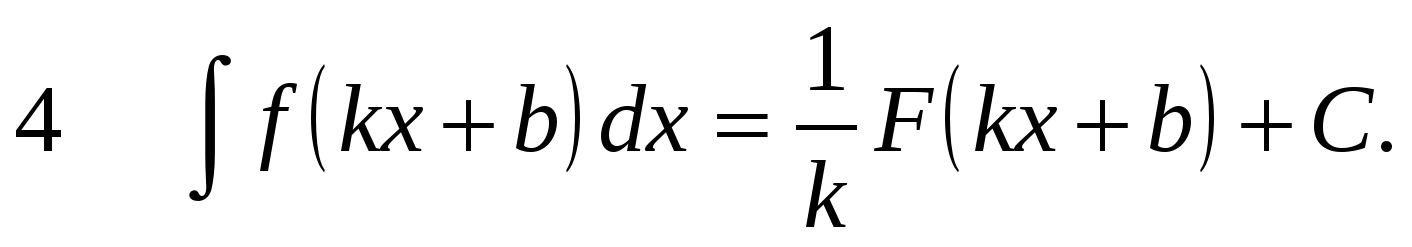
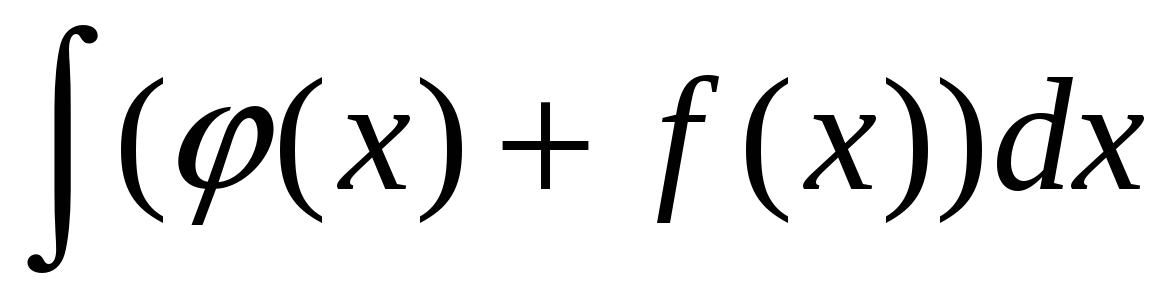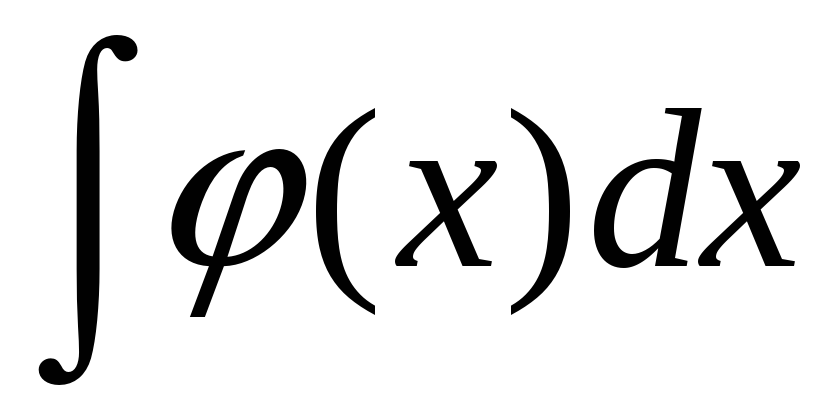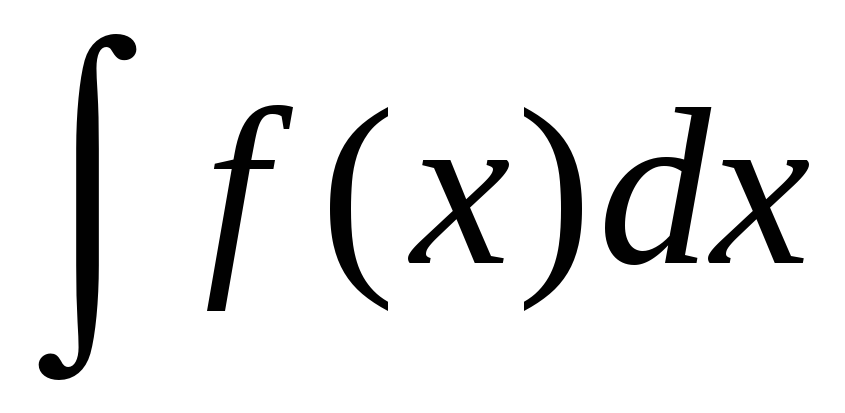Таблица первообразных или основные формулы интегрирования

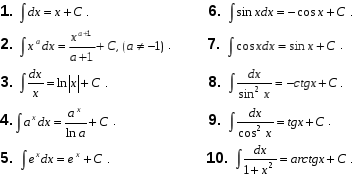
Пример. 3)

Найти общий вид первообразной для функции .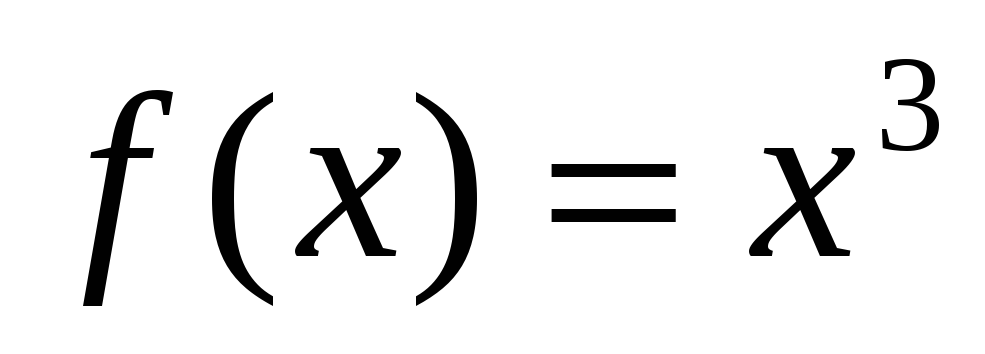

Т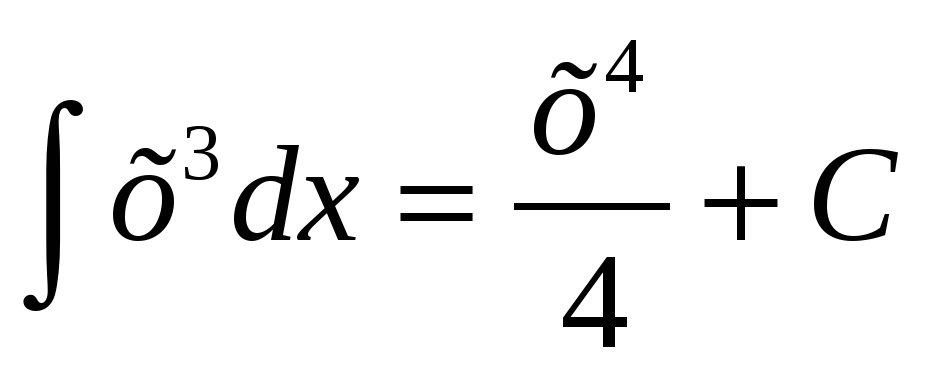.е. необходимо воспользоваться определением неопеределнного интеграла,

и 2 формула в таблице интегралов. проверка

Пример. 4)

Найти общий вид первообразной для функции .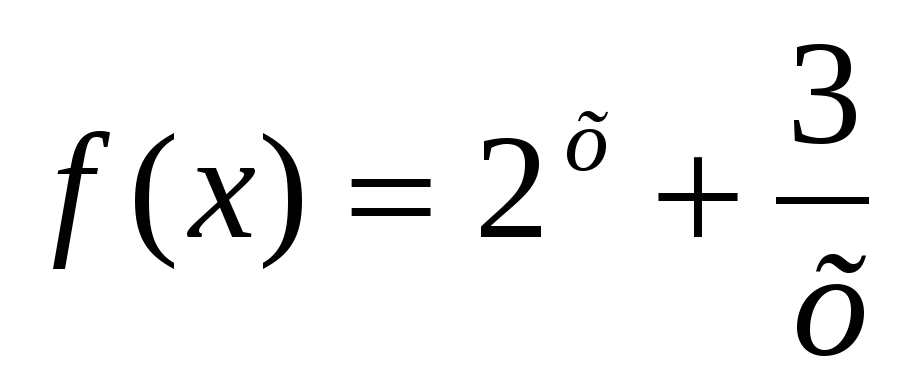

Т.е. необходимо воспользоваться определением неопеределнного интеграла,

с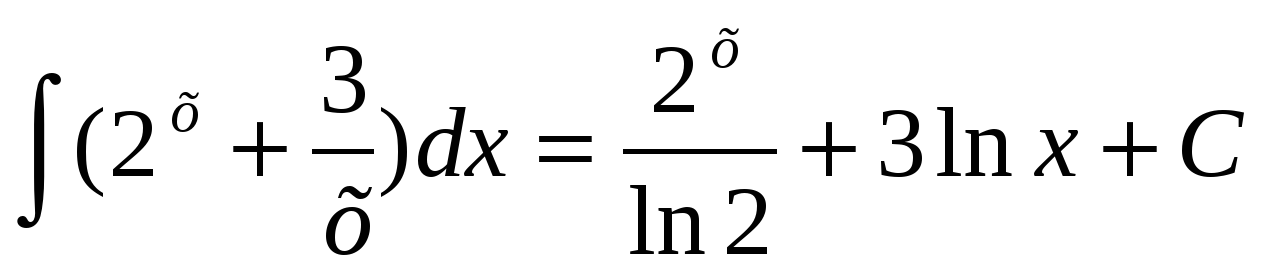войство 3 и формула 3 и 4 по таблице первообразных. Проверка

Пример. 5)

Найти общий вид первообразной для функции .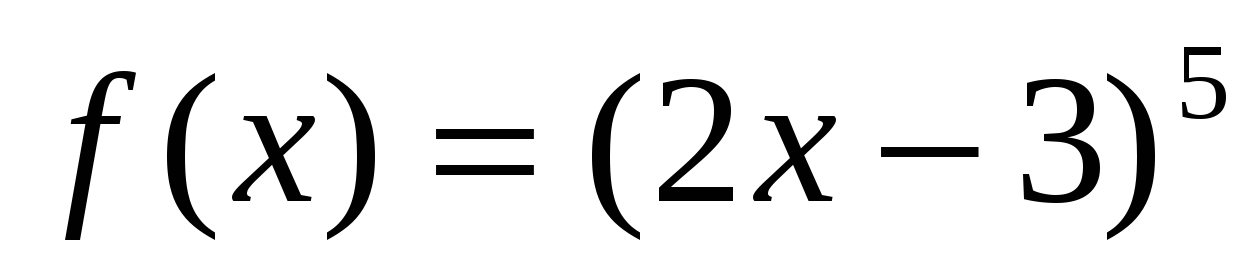

Т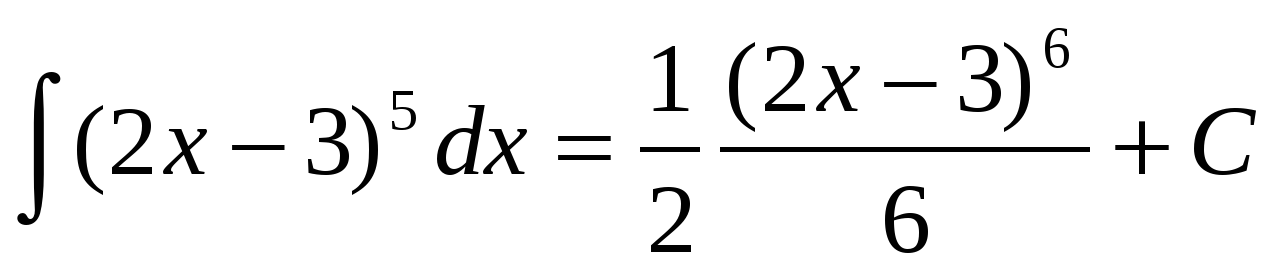.е. необходимо воспользоваться определением неопеределнного интеграла,

свойство 5 и формула 2

4. Тақырыптың негізгі ұғымдарын бекіту бойынша жұмыс:

Работа по закреплению основных понятий темы:

Решить задания № 327(а,б), №335(а,б) по закреплению нового материала.

5. Қорытынды жасау:

Выводы:

Устный опрос изученного теоретического материала.

1. Что называется интегрированием?

2. Объясните понятие первообразной функции.

3. Что подтверждает существование нескольких первообразных?

4. Что мы называем определенным интегралом?

5. Какие существуют свойства неопределенного интеграла?

6. Таблица производных?

Выставление оценок.

6. Үй тапсырмасын беру:

Задание на дом:

Выучить конспект определения, теорему и таблицу неопределенных интегралов. Выполнить задание № 327 (в,г), №336(а,б) по Колмогорову А.Н.

.