Разработка урока по теме "Координатная плоскость"

17.05.2016

Урок в 6 а классе по теме

«КООРДИНАТНАЯ ПЛОСКОСТЬ»

Учитель математики

Прус И.И.

Цели урока:

• познакомить учащихся с новыми понятиями: “координатная плоскость”, “система координат”, “прямоугольная система координат”, их использование в практических целях и в жизни человека;

• научить учащихся пользоваться системой координат, находить координаты заданных точек, и по заданным координатам точки определять ее положение на координатной плоскости;

• закрепить полученные навыки на практике при решении отдельных примеров и задач;

• активизировать внимание учащихся с помощью применения мультимедийных средств;

• воспитывать интерес к предмету.

Задачи:

- обучающие: 1) ввести понятие координатной плоскости;

2) научить учащихся строить точки на координатной плоскости;

3) научить учащихся определять координаты точек, построенных на координатной плоскости.

- развивающие: развитие логического и математического мышления, четкости и аккуратности выполнения.

- воспитательные: развитие интереса к предмету.

Тип урока: изучение нового материала

Оборудование: рабочая тетрадь, линейка, карандаш, мультимедийный проектор, презентация к уроку, карточки с заданием.

Ход урока

1. Организационный момент. Сообщение темы, целей и задач урока. Проверка всех нужных инструментов и учебных пособий для урока.

Учащиеся записывают дату проведения урока, тему урока «Координатная плоскость».

Вопросы для повторения:

1) какие две прямые называются перпендикулярными?

2) Как расположена прямая, перпендикулярная горизонтальной прямой (вертикальной прямой)?

3)

2. Объяснение нового материала.

Общаясь друг с другом, люди часто говорят: "Оставьте свои координаты". Для чего?...Чтобы человека было легко найти. Это могут быть: номер телефона, домашний адрес, место работы, Е-mail. Главное здесь в том, что по этим данным человека можно найти.

Суть координат или системы координат состоит в том, что это правило, по которому определяется положение объекта.

Системы координат окружают нас повсюду, пронизывают всю практическую жизнь человека. Кроме почтовых адресов и номеров телефонов, вспомним с какими системами координат вы знакомы?

• При посещении театра: чтобы правильно занять свое место в кинотеатре нужно знать две координаты - ряд и место;

• При поездке в поезде: чтобы найти свое место в поезде сначала мы ищем свой вагон, затем номер своего места;

• При игре в шахматы : вертикали – цифры, горизонтали – латинские буквы.

• При игре в морской бой: каждая клетка на игровом поле определялась двумя координатами - буквой и цифрой;

На уроках географии: система географических координат (широта - параллели и долгота - меридианы);

• Взрослые используют это понятие для определения местоположения объектов:

• такого рода “клеточные координаты” обычно используются на военных, геологических картах.

• с помощью координатной сетки летчики, моряки определяют местоположение объектов;

• применяются на туристических схемах для поиска достопримечательности или нужной улицы;

• при астрономических наблюдениях координатная сетка накладывается на небесный свод с Землей в центре

Термин “координаты” произошел от латинского слова и означает – упорядоченный.

Исторический материал

- Как давно системы координат пронизывают практическую жизнь человека? Идея координат зародилась еще в древности.

Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.

Во II веке н.э. знаменитый древнегреческий астроном Клавдий Птолемей уже пользовался долготой и широтой в качестве географических координат.

Но эти понятия впервые были систематизированы в 17 веке Рене Декартом.

Рене Декарт (1596-1650) - французский философ, естествоиспытатель, математик. Автор координатной плоскости. В 1637 году Рене Декарт впервые опубликовал изложение метода координат, поэтому прямоугольную систему координат часто называют «декартовой системой координат».

Координатная плоскость

При изучении темы “Координатная прямая”, мы научились находить по координате положение точки на прямой.

- Как задаются координаты на прямой. (На прямой выбирают начало отсчёта, положительное направление и единичный отрезок). После этого любая точка прямой получает свою собственную координату. Например, точки А,В,С, имеют соответственно координаты А(-2), В(3), С(-4)).

- Таким образом, координата точки указывает, её место на координатной прямой.

Постановка проблемного вопроса.

А как указать положение точки на плоскости?

Наводящие подсказки (морской бой, шахматы, чем отличается шахматная доска от плоскости, повторить определение плоскости).

- Таким образом, сколько координат нужно задать, для того чтобы указать положение точки на плоскости?

- Вы уже догадались, что для того, чтобы определить положение какой-либо точки на плоскости необходимо знать две ее координаты. Для этого на плоскости строится система координат.

.

Координатная плоскость. Рассмотрим ее составляющие:

• две перпендикулярные прямые - оси координат:

• вертикальная ось – ось абсцисс (ось X), горизонтальная ось – ось ординат (ось Y), стрелки осей указывают положительные направления,

• начало координат- точка О-  точка пересечения прямых,

• на прямых, вводят обычные координаты, которые согласованы между собой.

Плоскость, на которой задана система координат, называется координатной плоскостью.

Термины «абсцисса» и «ордината» (лат. «отсекаемый» и «упорядоченный») были введены в 70-80 годы XVIв. нем. математиком Вильгельмом Лейбницем.

Нахождение координат точек.

Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса (х) и ордината (у). И наоборот, каждой паре чисел (х; у) соответствует единственная точка на плоскости. Координаты точки записывают в скобках через точку с запятой, причем первой всегда записывается координата х, второй координата у. Из точки опускаем перпендикуляр на ось X получаем абсциссу x; опускаем перпендикуляр на ось Y получаем ординату y.

Применим изученный материал на практике:

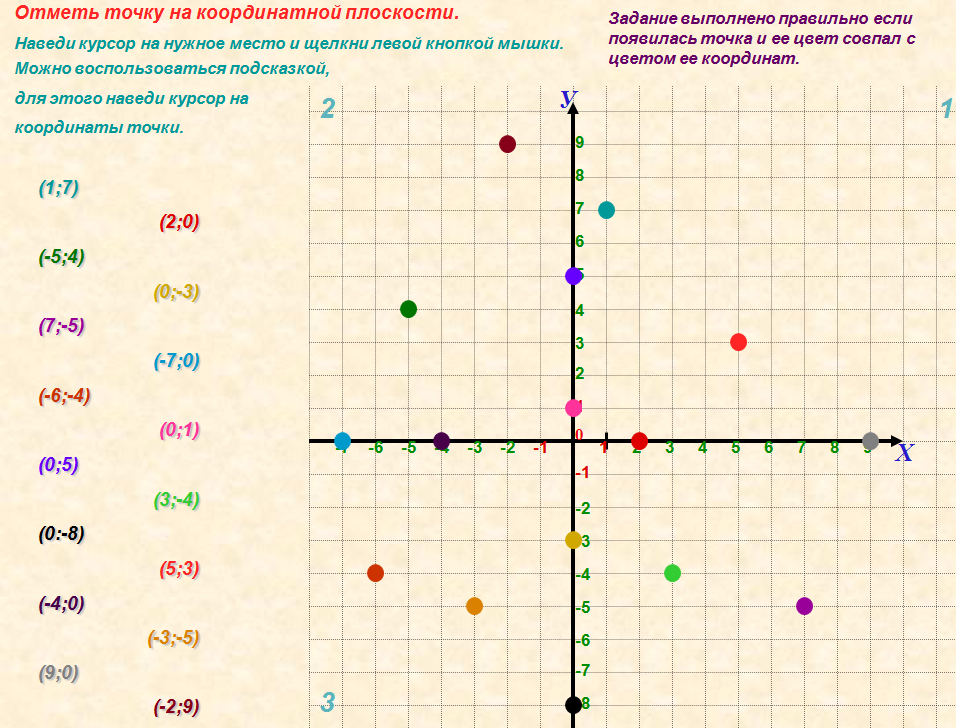
Задание: по рис. определите координаты точки (карточки с заданиями раздаются)

А(2;2) В(4;1) С(2;-2) D(-4;2) E(-2;-4) F(-1;4) G(-2;-2) M(3;0) P(0;3) N(-2;0) O(0;-2) K(4;-2)

Построение точек на плоскости по заданным координатам.

Построим точки А (3;5), B(-3;-2), C (0;4), D (-3;0), K (1; -2), L (-3; 5).

Координатные четверти. Выполнить рис на доске. (Если позволит время)

Плоскость, на которой задана система координат, называется координатной плоскостью. Оси координат разбивают ее на 4 координатные четверти. Нумеруются они против часовой стрелки.

Если точка лежит в 1 четверти, то имеет положительные абсциссу и ординату.

Если во 2 четверти, то имеет отрицательную абсциссу и положительную ординату.

Если во 3 четверти, то имеет отрицательную абсциссу и ординату.

Если во 4 четверти, то имеет положительную абсциссу и отрицательную ординату.

Задание: по координате точки определить в какой координатной четверти она расположена

(-5;-3) - III четверть

(-7;3) – II четверть

(10;-2) - IV четверть

(-6;0) - граница II и III четвертей

(5;0) - граница I и IV четвертей

(0;-7) - граница III и IV четвертей

(9;3) – I четверть

(-5;0) - граница II и III четвертей

(0;-1) – граница III и IV четвертей

(7;4) – I четверть

(0;10) – граница I и II четвертей

(-5;-3) – III четверть

(9;0) –граница I и IV четвертей

(-5;7) – II четверть

(0;3) – граница I и II четвертей

4. Закрепление изученного материала

Тест «Координаты на плоскости» (либо фронтальная работа по ответам на вопросы)

1. Под каким углом пересекаются координатные прямые, образующие систему координат на плоскости?

• под острым углом

• под прямым углом

• под тупым углом

• под развернутым углом

1. Как называется горизонтальная прямая?

• аппликата

• ордината

• абсцисса

• биссектриса

1. Как называется вертикальная прямая?

• ордината

• абсцисса

• аппликата

• биссектриса

1. Как называют точку пересечения этих прямых?

• начало всех начал

• середина

• начало отсчета

• разделитель

1. Как называют пару чисел, определяющих положение точки на плоскости?

• координаты точки

• числа на плоскости

• числа для точки

• показатели точки

1. Что показывают стрелки на координатных прямых?

• что прямые можно продолжить

• положительное направление

• отрицательное направление

• ничего не показывают

1. В какой координатной четверти может находиться точка, имеющая координаты с разными знаками?

• в 1 или во 2

• только во 2

• во 2 или в 3

• во 2 или в 4

1. Как правильно записываются координаты?

• (х;у)

• (у;х)

• х,у

• в любом порядке

5. Итог урока.

В ходе урока мы научились отмечать точки с заданными координатами на координатной плоскости и наоборот определять координаты точек заданных на координатной плоскости.

Учитель: А знаете ли вы, что в координатной плоскости можно не только отмечать точки с заданными координатами, но также можно создавать различные картинки? (Показать папку). Для этого необходимо отметить точки с заданными координатами и последовательно соединить их отрезками.

Домашнее задание. п. 44. Карточки с заданиями: По заданным координатам нарисовать картинки. На следующем уроке устроим выставку.