Разработка урока по теме Линейная функция и её график. Свойства линейной функции.

Дата: 3.04.2017 год

Предмет: математика

Класс: 6 урок №160

Сабақ тақырыбы/Тема урока: «Линейная функция и её график. Свойства линейной функции».

Сабақ мақсаты/цели урока:

Білімділік/образовательные: Ввести определение линейной функции. Научить строить график линейной  функции. Познакомить учащихся со свойствами линейных

функций.

Дамытушылық/развивающие: Учить обобщению, систематизации знаний,  делать выводы, сравнивать, анализировать.

Тәрбиелік/воспитательные: Воспитывать аккуратность, наблюдательность, самостоятельность.

Сабақ барысы:/ Ход урока:

1.Организационный момент.

    Здравствуйте,  ребята. Садитесь.                          

2. Постановка цели и мотивация.

Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:

             - Что есть больше всего на свете? – Пространство.

             - Что быстрее всего? – Ум.

             - Что мудрее всего? – Время.

             - Что приятнее всего? – Достичь желаемого.

Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.

3. Актуализация опорных знаний.

Как называется переменная х, и переменная у?

 Сколько координат имеет точка на координатной плоскости?

 Постройте на координатной плоскости точки: А(2;-3), В(-4;0), С(-2;5), Т(1;4). В каких четвертях лежат эти точки?

 Чтобы провести прямую, сколько точек нужно знать?

4. Изучение нового материала.

а) Понятие функции первоначально возникло из решения задач. Давайте и мы решим несколько задач.

Задача 1. Мама купила несколько конфет (d) по 5 рублей за конфету и одну шоколадку за 65 рублей. Сколько она заплатила за всю покупку (n)?

От чего зависит стоимость всей покупки?

Составьте выражение.

Задача 2. На шоссе расположены пункты А и В, удаленные друг от друга на  20 км. Мотоциклист выехал из пункта В в направлении, противоположном А, со скоростью 50км/ч.

На каком расстоянии S(км) от пункта А будет мотоциклист через t часов?

От чего зависит S от А до места нахождения мотоциклиста, если  его скорость постоянная?

б) В обеих задачах была зависимость одной величины от другой. Такую зависимость называют функцией. В общем виде её можно записать так: у=кх+b, где к и b некоторые числа, х – независимая переменная, у – зависимая переменная. Такая зависимость называется линейной функцией. Независимая переменная называется аргументом, зависимая – значением функции. Функцию обозначают у или f(x).

Примеры записи линейной функции: (назвать значения к и b, зависимую и независимую переменные)

У=2х-1;      у=0,5х+3;   f(x)=х-0,3;   f(x)=-2,5х.

в) Вопрос учащимся: Как вы думаете, какие значения можно брать для значений аргумента? Предполагаемый ответ (положительные, отрицательные и нуль) . 

А какие при этом будут получаться значения функции? Ответ аналогичный.

Вывод: Значит, значения аргумента, и значения функции могут принимать любые значения.

Все значения аргумента функции, при которых она имеет смысл, называют областью определения функции и обозначают D(y). Все значения функции называют областью значений функции и обозначают Е(у). Так как значения аргумента и значения функции для линейной зависимости могут быть любыми числами, то и D(y) и  E(y) любые числа.

Сегодня на уроке мы установим, какой вид имеет график линейной функции, и научимся его строить.

Построим график линейной функции y = 2x – 1. Для этого составим таблицу значений функции с шагом 1 при -3 ≤ x ≤ 3.

    (ученики заполняют таблицу самостоятельно, а затем проверяют результаты вычислений).

Отметим в координатной плоскости точки, координаты которых указаны в таблице.

Чтобы построить график функции, надо найти координаты точек этой функции, отметить их в координатной плоскости и провести через них линию, которая является данной функции.

Соединим точки линией и получим отрезок. Работа по графику: свойства линейной функции.

Вывод: (учащиеся делают сами) были даны разные линейные функции, но в каждом примере её графиком является прямая, поэтому для построения графика линейной функции можно найти координаты двух точек.  Графиком функции является прямая.

Линейной функцией называется функция вида y=kx+b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.

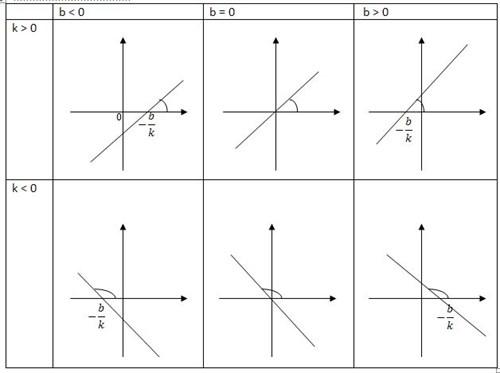
В уравнении функции y=kx+b коэффициент k отвечает за наклон графика функции:

• если k>0 , то график наклонен вправо;
• если k<0 , то график наклонен влево.

Коэффициент b отвечает за сдвиг графика вдоль оси OY:

• если b>0 , то график функции y=kx+b получается из графика функции y=kx сдвигом на b единиц вверх вдоль оси OY;
• если b<0 , то график функции y=kx+b получается из графика функции y=kx сдвигом на b единиц вниз вдоль оси OY.

Графики линейных функций, заданных формулами вида y=kx+b, пересекаются, если коэффициенты при x различны, и параллельны, если коэффициенты при x одинаковы.

Взаимное расположение графиков функции

5.  Первичное закрепление нового материала.

1. Найдите точку пересечения графика функции y=13x+1 с осью OX.
2. Найдите точку пересечения графика функции y=5x+10 с осью OY.
3. График функции y=kx+b проходит через точки A(–4;3) и B(4;9). Найдите значения k и b.
4. Найдите точку пересечения графиков функций y=5x−3 и y=3x+1.
5. При каком значений аргумента функция y=23x будет равна -4?

6. Физкультминутка.

Что ж, пора немного отдохнуть. Приглашаю всех на разминку.

Сядьте ровно. Покажите мне руками маленькую окружность. А теперь представьте, что наша окружность раздувается, становится все больше и больше. Показываем, вот какая получилась окружность. А теперь поднимаем эту окружность над собой и держим над головой. Представим, что подул ветер и наша окружность наклоняется сначала влево, потом вправо. А теперь представим, что окружность превратилась в воздушный шарик и отпускаем ее. Молодцы!

7. Работа с учебником.

№ 1327, №1328(устно), №1330, №1331, №1333(5,6) решение у доски с комментарием.

7. Подведение итогов.  Домашнее задание. Рефлексия.

П.8.4, Решить № 1332, №1333(1-4)

•  Какой формулой задается линейная функция?
•  Что является графиком линейной функции?
•  Перечислите, какие свойства линейной функции мы рассмотрели на уроке?
•  Что нужно знать, чтобы построить график линейной функции?
•  Как определить, не выполняя построения, проходит ли заданная прямая через заданную точку?

Прежде, чем мы окончим урок, я хочу узнать, что же изменилось или сохранилось в вашем настроении в течение урока.  И поэтому попрошу вас ответить на вопросы:

• Я научился…
• Было трудно…
• Сегодня я узнал…
• У меня получилось…
• Теперь я могу…

Спасибо за урок до свиданье!