Разработка урока по теме: « Теорема Виета»
Никогда не теряй терпенья – это
последний ключ, который открывает
двери.
Антуан де Сент-Экзюпери.
Описание работы:
Конспект урока предназначен для педагогов, работающих по учебнику Алгебра, 8 Ю.Н. Макарычев, Н.Г.Миндюк под редакцией С.А. Теляковского. В ходе проведения урока учащиеся проведут небольшую исследовательскую работу на установление зависимости между корнями приведенного квадратного уравнения. На данном уроке учащиеся познакомятся с теоремой Виета и будут учиться ее применять при нахождении корней квадратных уравнений.
Образовательные цели урока:
- повторить решение квадратных уравнений;
- раскрытие связей между корнями квадратного уравнения и его коэффициентами;
- изучить теорему Виета;
- рассмотрение различных заданий на применение теоремы Виета.
Развивающие цели урока:
- .Развивать и совершенствовать умения применять учащимися знания и умения в новой ситуации;
- развивать умения делать выводы и обобщения.
Воспитательные цели:
- Воспитание интереса к предмету через познавательные сюжеты из истории математики:
- воспитывать самостоятельность.
Тип урока: урок усвоения новых знаний
Ход урока
1.Организационный момент
Проверка готовности к уроку. Приветствие. Мы с вами изучаем квадратные уравнения и способы их решения. Сегодня мы познакомимся с еще одним методом решения квадратных уравнений.
2. Актуализация опорных знаний
- Какое уравнение называется квадратным?
- Какие существуют виды квадратных уравнений?
- Что значит решить уравнение?
- Сколько корней может иметь квадратное уравнение?
- От чего зависит наличие действительных корней квадратного уравнения?
4. Формирование новых знаний.
Задание.
Решить уравнение х2 + 5х + 6 = 0 х=-2, х=-3
Найти сумму и произведение корней уравнения: (-2)+(-3)=-5, а (-2)*(-3)=6
– Какое квадратное уравнение вы решили?
– Какую зависимость между корнями и коэффициентами вы заметили?
(Учащиеся делают выводы)
Да, действительно, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение – свободному члену. Вот в этом и заключается теорем Виета.
Впервые зависимость между корнями и коэффициентами квадратного уравнения установил
знаменитый французский ученый Франсуа Виет (1540-1603)
Если х1, х2 – корни квадратного уравнения аx2 + bx + c = 0,
то х1 + х2 = -- ; х1 ∙ х2 = .
; х1 ∙ х2 = .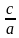 .
.
Франсуа Виет (1540-1603) – крупнейший французский математик XVI века. Юрист по образованию. Виет увлекался астрономией и занимался усовершенствованием тригонометрических таблиц. Он был советником короля Генриха III,которому помог в расшифровке переписки его врагов с испанским двором, он раскрыл тайну шифра, состоявшего из 500 знаков. Свои алгебраические идеи Виет изложил в сочинении «Введение в аналитическое искусство», в котором предложил преобразовать алгебру в мощное математическое исчисление. Виет ввел систему алгебраических символов, разработал основы элементарной алгебры, он был одним из первых, кто числа стал обозначать буквами, что существенно развило теорию уравнений.
А чтобы лучше запомнить, необходимо выучить стихотворение:
Теорема Виета
Поэтом по праву должна быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого-
Умножишь ты корни и дробь уж готова:
В числителе с, в знаменателе а
И сумма корней тоже дроби равна,
Хоть с минусом дробь та, но что за беда:
В числителе в, в знаменателе а.
Доказательство теоремы Виета.
Для приведенного квадратного уравнения, х2 + pх + g = 0, где x₁ + x₂ = - p, а x₁ * x₂= g. Применяя теорему Виета, результат запишем в таблицу:
| Алгоритм | Доказательство |
| 1.Записать формулы для нахождения x₁ и x₂ | x₁ =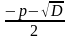 , x₂ = , x₂ = 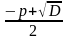 , D= , D=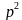 -4q -4q |
| 2.Найти сумму корней: x₁+ x₂;
| x₁+ x₂ =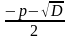 + + 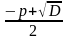 = -p = -p |
| 3.Найти произведение корней: x₁· x₂ | 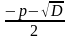 . . 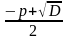 = =  = q = q
|
Справедливо утверждение обратное теореме Виета. Сформулируйте это утверждение
5. Формирование умений и навыков.
1. (Устно) Выберите среди данных уравнений приведенные квадратные уравнения:
а) 2х2 + 3х – 1 = 0 б) х2 – х – 6 = 0 в) 3х2 + 5 = 0 г) х2 + 7х + 6 = 0
2. (Устно) Чему равны сумма произведения корней уравнения:
а) х2 + 7х + 6 = 0 б) х2 – 8х + 12 = 0 в) х2 – х – 6 = 0
3. Пусть х1 и х2 – корни квадратного уравнения:
а) х1 = 4; х2 = -3 в) х1 = -3; х2 = -6
б) х1 = 5; х2 = -6 г) х1 = 8; х2 = 12
Применяя теорему Виета составьте квадратные уравнения по их корням.
4. Определите корни квадратного уравнения, пользуясь теоремой, обратной теореме Виета
а) х2 + 7х + 6 = 0
б) х2 – 8х + 12 = 0
в) х2 – х – 6 = 0
5. Самостоятельная работа по вариантам. После окончания работы решения проверяются с помощью проектора.
Вариант I.
1. Пусть х1 и х2 – корни квадратного уравнения. Решите уравнения (а – к), запишите корни уравнения в указанном порядке (при решении там, где это удобно, пользуйтесь теоремой, обратной теореме Виета).
а) х2 – 25 = 0, (5;-5)
б) х2 – 3х = 0, (0;3)
в) х2 – 5х + 6 = 0, (3;2)
г) х2 – 12х + 35 = 0, (7;5)
д) х2 – 6х = 0, (0;6)
е) х2 – 2х – 35 = 0, (7;-5)
ж) х2 – х – 6 = 0, (3;-2)
з) х2 + 3х =0, (0;-3)
и) х2 + 10х + 25 = 0, (-5;-5)
к) х2 + 10х = 0, (0;-10)
2. Один из корней уравнения х2 + рх – 35 = 0 равен 7. Найдите другой корень уравнения и коэффициент р.
Вариант II.
1. Пусть х1 и х2 – корни квадратного уравнения (х1 2). Решите уравнения (а – к), запишите корни уравнения в указанном порядке (при решении там, где это удобно, пользуйтесь теоремой, обратной теореме Виета).
а) х2 – 4х – 21 = 0, (-3;7)
б) х2 – 10х + 21= 0, (3;7)
в) х2 – 7х + 12 = 0, (3;4)
г) х2 – 6х = 0, (0;6)
д) х2 + 4х – 32 = 0, (-8;4)
е) х2 + 6х – 55 = 0, (-11;5)
ж) х2 + 16х + 55 = 0, (-11; -5)
з) х2 + 12х + 32= 0, (-8; -4)
и) х2 + 6х =0, (-6; 0)
к) х2 – х – 12 = 0, (х1; х2)
2. Один из корней уравнения х2 – 13x + q = 0 равен 12,5. Найдите другой корень уравнения и коэффициент q.
6.Подведение итогов:
Рефлексия.
Ответьте на вопросы:
– Какие уравнения мы сегодня рассмотрели?
– Чему равна сумма корней квадратного уравнения?
– Чему равно произведение корней квадратного уравнения?
Продолжите фразы:
– Сегодня на уроке я узнал …
– Сегодня на уроке я научился …
– Сегодня на уроке я познакомился …
– Сегодня на уроке я повторил …
– Сегодня на уроке я закрепил …
7.Домашнее задание.
Решить №582, 584(б),586(а,г)
8. Творческое задание
Решить уравнение: 4х2 - 5х + 1 = 0
Написать квадратное уравнение, корни которого равны: а) х1+ 1 и х2 + 1; б) х1- 2 и х2 – 2.


























