ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ДОПОЛНИТЕЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНЕЦКИЙ РЕСПУБЛИКАНСКИЙ ИНСТИТУТ
ДОПОЛНИТЕЛЬНОГО ПЕДАГОГИЧЕСКОГО ОБРАЗОВАНИЯ»
ВЫПУСКНАЯ РАБОТА
Развитие творческих способностей учащихся
на уроках математики
Ковалева Ирина Вадимовна
учитель математики МОУ «Школа № 2 города Донецка»
код курсов 9.4
Тема курсов: Современный урок с учетом требований новых государственных образовательных стандартов
Руководитель курсов:
Полищук Ирина Валерьевна
Методист отдела математики, старший преподаватель кафедры естественно - математических дисциплин и методики преподавания
2017
СОДЕРЖАНИЕ
Вступление…...………………………………………………………3
Развитие творческих способностей школьников …………………7
О математическом творчестве………………………………..7
Развитие творческих способностей учащихся
на уроках математики……………………………………..…..9
Развитие творческих способностей учащихся с применением интерактивных методов обучения …………12
Развитие творческих способностей
на факультативных занятиях по математике………….…..16
Применение теоретических наработок в практической
деятельности учителя……….……………………………………..18
Заключение ………..……………………………………………….30
Литература ………………..………………………………………..21
ВСТУПЛЕНИЕ
В настоящий момент происходит реформирование системы образования Донецкой Народной Республики в соответствии в Государственными Образовательными Стандартами. Реформирование касается и новых образовательных стандартов, и обновления учебных программ, и содержания учебников, и новых методов и форм обучения. Целью реформ является принципиально новый подход к учебно-воспитательному процессу. Результатом учебной деятельности учащихся должна стать не сумма приобретенных знаний, умений, навыков, а компетентность ученика, которая не ограничивается содержанием определенной школьной дисциплины. Результатом учебной деятельности ученик должна стать не просто информация, а умение ее применять, использовать в определенных ситуациях, решать различные практические и теоретические задачи, ориентироваться в конкретных жизненных ситуациях, сотрудничать и работать в команде, решать конфликты, умение применять информационные и коммуникационные технологии. Именно поэтому понятие компетентности является очень важным. Важно осознать, что должно стать результатом обучения, и как этого достичь.
Творческий труд в нашем сложном и многогранном деле начинается там, где загорается искра живой, трепетной мысли, ищущей ответ на вопрос, который выдвигает жизнь. Вопрос, зажигающий искру творчества, возникает тогда, когда мы хотим видеть итог своих многодневных стараний, хотим видеть результаты своего труда лучшими, чем они есть в настоящее время, когда не дает покоя мысль: почему учения не приводят к тому, к чему они, казалось бы, должны привести? Почему большой проблемой подростка является охлаждение, часто равнодушие к учебе, а то и просто нежелание учиться? Одна из главных причин этого явления – отсутствие или убогость творческого начала в духовной жизни. Подростку уже мало мех стимулов, которых было достаточно для младшего школьника: выполнения воли и желания дорогого человека, похвалы, поощрения. Подросток стремится выразить себя, и выразить не только в результатах своей учебы, но и во внутреннем духовном мире. Ему уже не хочется быть пассивным потребителем духовных благ и ценностей. Он хочет быть творцом. Творческое равновесие трудом, создающим какие-то духовные ценности, является важнейшим условием полноты его духовной жизни. Творческое вдохновение – человеческая потребность, в которой личность находит счастье. Переживая духовное удовлетворение от того, что он творит, человек по-настоящему ощущает, что он живет. Творчество начинается там, где интеллектуальные и эстетические богатства, освоенные, добытые раньше, становятся средством познания, освоения, преобразования мира, при этом человеческая личность словно сливается со своим духовным достоянием.
Важнейшим первоисточником творчества как самовыражения и самоутверждения личности является слово. И творческое вдохновение, которое переживается уже в детские годы, начинается с того, что слово как духовное богатство личности становится строительным материалом, из которого ребенок что-то создает. Задача учителя – увидеть и развить эти творческие порывы учеников. В наше время кардинального изменения и учителя и ученика необходимо помочь детям в развитии творческого подхода к приобретению знаний и духовного развития.
Актуальность проекта:
Актуальным для каждого учителя сегодня является вопрос: “Как учить?” Как включить учеников в учебно-познавательную творческую деятельность, чтобы они сами “открывали” новые свойства и отношения, а не получали их от учителя в готовом виде.
Важность проблемы – развитие творческого потенциала учащихся – обусловлена двумя основными причинами:
- первая из них – падение интереса к учебе. Уже к концу десятилетнего обучения, как показывают различные психологические опросы, интерес к учебе сохраняют от 20 до 40% учащихся,
- вторая причина в том, что даже те ученики, которые, казалось бы, успешно справляются с программой, теряются, как только оказываются в нестандартной учебной ситуации. Поэтому свою цель как учитель математики я вижу не только и не столько в том, чтобы передать ученикам определенный объем знаний, но главное – в развитии их творческих способностей.
Главным критерием деятельности учителя является конечный результат: смогли ли мы дать ученику определенную сумму знаний по предмету или удалось ли нам сформировать личность, готовую к творческой деятельности и саморазвитию. Только тогда, когда учебная деятельность, направленная на овладение основами наук и на развитие личностных качеств, сформирована на более высоком уровне, начинает ясно проявляться ее творческая сторона. Очень важно развивать у учащихся творческие способности, независимо от того, хорошо ребенок учиться или не очень. А такие способности есть у каждого ученика. Задача учителя – вовремя заметить и поощрить стремление ребят к творчеству и развитию способностей, изначально заложенных природой.
Цели проекта:
- Поддерживание интереса к предмету;
- Развитие качеств творческой личности: познавательной активности, усидчивости, упорства в достижении цели, самостоятельности;
- Формирование и дальнейшее развитие мыслительных операций: анализа и синтеза, сравнения, обобщения;
- Развитие мышления вообще и творческого в частности;
- Подготовка учащихся к творческой деятельности;
- Умение переносить знания в незнакомые ситуации.
Поэтому развитие инициативы, творческих начал является первейшей задачей каждого педагога. Преподавание математики в школе было всегда сопряжено со многими проблемами. Выявление и развитие потенциала каждого ученика, раскрытие его творческих способностей требуют учета индивидуальных особенностей мышления учащихся в процессе обучения математике. Для учителя важна максимальная ориентация на творческое начало в учебной деятельности учащихся в частности, на потребность и умение самостоятельно находить решение не встречавшихся ранее учебных задач. Важнейшим элементом в его деятельности является работа над содержанием, которая включает глубокое продумывание учебного материала и выявление существенных связей не только внутри одной темы, раздела, но и по всему курсу школьного математического образования. Возникает потребность усиления гуманистической, общечеловеческой направленности математики, обеспечения активного творческого включения учащихся в процесс освоения математического материала. Учителю нужно стараться замечать и поощрять малейшие успехи детей, не подвергать осуждению, критике их неудачи и промахи.
Задачи проекта:
поддерживать и развивать интерес к предмету;
прививать навыки учебно-исследовательской работы;
развивать логическое мышление, пространственное воображение учащихся;
учить основам самообразования, работе со справочной и научной литературой, с другими современными источниками информации;
показывать практическую направленность знаний, видеть роль и место математики в повседневной жизни, ее связь с другими науками.
РАЗВИТИЕ ТВОРЧЕСКИХ СПОСОБНОСТЕЙ ШКОЛЬНИКОВ
. О математическом творчестве.
Прогресс человечества неразрывно связан с творчеством, с созданием нового, с возникновением идей, позволяющих взглянуть на, казалось бы, хорошо известные явления с неожиданных позиций. Творчество необходимо во всех областях деятельности, а не только в науке, проектировании, литературном и художественном труде. Те, кто сейчас учится в школе, через несколько лет вступят в самостоятельную жизнь и начнут работать в различных отраслях народного хозяйства. На и плечи ляжет обязанность не только поддерживать достижения экономики, науки и культуры, но и способствовать их совершенствованию. Для этих целей понадобится не только умение трудиться и увлеченность делом, но и расцвет талантов и творческих способностей. Но для того, чтобы потенциальные творческие таланты пробудить к жизни, необходимо систематически воспитывать учащихся в стремлении поиска лучших путей для выполнения порученного дела, творчески овладевать содержанием курса школьного обучения.
Что такое творчество? Как проявляются творческие способности? В 1959 году американский психолог Фромм предложил следующее определение понятия творчества: “Это способность удивляться и познавать, умение находить решения в нестандартных ситуациях, это нацеленность на открытие нового и способность к глубокому осознанию своего опыта”.
Воспитывать вдумчивого, творчески мыслящего, заинтересованного в своем труде человека – одна из основных задач, стоящих перед школой. Ошибкой было бы начинать приобщать ученика к творчеству лишь после того, как он овладеет основами наук. Ребенок, обучаясь, должен иметь возможность творить, фантазировать на доступном ему уровне и в известном мире понятий. А если он к тому же свободен от боязни ошибиться, то всё это станет залогом успеха начинающейся творческой деятельности.
Многие крупные мыслители полагают, что некоторые лица обладают специфическими творческими задатками, и что успех человека в той или иной сфере деятельности во многом зависит именно от наличия этих задатков. В связи с этим можно привести небольшую цитату из статьи А.Н.Колмогорова: «Талант, одаренность, скажем, в области математики, физического эксперимента, конструирования новых приборов даны от природы не всем. Никакой упорный труд не может заменить эту природную одаренность. Он дает действительно ценные плоды в науке лишь в соединении содаренностью, как, конечно, и одаренность окажется бесплодной без упорного и сосредоточенного труда».
В то же время следует сказать ,что математическая одаренность встречается не так редко, как это многим кажется. Но эта творческая жилка проявляется у разных лиц по-разному и в различных направлениях. Одни находят обобщение ранее полученных результатов и тем самым расширяют поле их применимости. Другие умеют найти совсем новые объекты для исследования. Третьи сильны в логическом совершенствовании теории. Четвертые находят решения глубоких прикладных проблем и открывают пути решения многочисленных вопросов в разнообразных областях знания. Следует принимать во внимание многообразие форм математического творчества и не пропустить ни одну из них. Отсутствие какой-нибудь одной из них еще не означает, что данное лицо полностью лишено творческих математических способностей.
Развитие творческих способностей требует длительного воздействия и должно быть предметом внимания педагогического коллектива. Каждый предмет школьного курсов способен внести свою долю воздействия на творческий облик учащегося. Математика представляет для этого исключительные возможности. Поиск решений нестандартных задач, нестандартных путей решения традиционных задач, размышления над парадоксами, поиск ошибок в рассуждениях, анализ содержания теорем и сути их доказательств, беседы о творческих лабораториях известных ученых – все это составляет важные слагаемые на пути развития способностей и духа творческого горения. Зачастую потенциально способный человек не имеет увлекательной и действительно важной задачи. Ему неоткуда ее получить, поскольку рядом нет коллектива, способного выдвинуть и развить полезную тематику. Способствующую прогрессу науки, производства, культуры. В результате у него нет объективной возможности проявить свои творческие способности.
В конце прошлого века прославила себя петербургская математическая школа в тот период, когда в Петербургском университете работал выдающийся ученый П.Л.Чебышев. Он охотно делился нерешенными задачами с молодежью, увлеченной наукой. И совсем не случайно Чебышев был как бы центром притяжения для способной молодежи, им была создана обстановка, благоприятствующая развитию талантов. Он предлагал им проблемы,которые увлекали их на долгие годы напряженной работы, интересовался их результатами, поддерживал их настроение.
В процессе воспитания творческого начала исключительно велика роль учителя, который способен направить учащихся на путь исканий, вызвать в них страсть поиска. Именно учитель помогает войти в атмосферу творчества, в круг идей,дающих большие возможности для самостоятельного поиска и для новых научных находок.
Развитие творческих способностей учащихся на уроках математики
Преподавание математики в школе было всегда сопряжено со многими проблемами. Выявление и развитие потенциала каждого ученика, раскрытие его творческих способностей требуют учета индивидуальных особенностей мышления учащихся в процессе обучения математике. Для учителя важна максимальная ориентация на творческое начало в учебной деятельности учащихся, в частности, на потребность и умение самостоятельно находить решение не встречавшихся ранее учебных задач. Важнейшим элементом в его деятельности является работа над содержанием, которая включает глубокое продумывание учебного материала и выявление существенных связей не только внутри одной темы, раздела, но и по всему курсу школьного математического образования. Возникает потребность усиления гуманистической, общечеловеческой направленности математики, обеспечения активного творческого включения учащихся в процесс освоения математического материала.
Процесс обучения должен строиться как совместная исследовательская деятельность учащихся — математическая истина (определённое правило, теорема, свойство) не сообщается ученикам “в готовом виде”, а открывается ими самими. Этот процесс начинается с наблюдений, высказывания догадок, суждений о возможном способе решения, о возможном содержании теоремы, правила, после чего следует проверка, поиски дедуктивного обоснования выводов, обобщение, анализ прикладных возможностей. Исследовательская или проблемная структура изучения математики хорошо отвечает развивающим целям обучения. Без определённой подготовки надеяться включить учащихся в успешную многоэтапную творческую поисковую деятельность нереально. Этот успех надо готовить.
В качестве примера рассмотрим работу по конструированию определения четырехугольника.
По заранее подготовленным на доске рисункам учащимся предлагается ответить на вопросы.





![]()







![]()

Вопросы классу:
Из скольких точек и отрезков состоит каждая из данных фигур?
Какая из этих фигур является четырехугольником?
Почему фигуру, изображенную на первом рисунке, нельзя назвать четырехугольником?
Почему не является четырехугольником фигура, изображенная на третьем рисунке?
Почему четырехугольником нельзя считать фигуру, изображенную на четвертом рисунке?
Очевидно, что не на все вопросы учащиеся сумеют дать точные ответы. В этом случае учитель сам дает нужные объяснения. Особенно это касается четвертого рисунка. Рассматривая фигуру, изображенную на этом рисунке, учащиеся могут обратить внимание на то, что у нее в точке В сходятся три отрезка, тогда как у четырехугольника в каждой из его точек сходятся только два отрезка. Комментируя этот факт, учитель поясняет, что если одну из данных точек соединить отрезком с другой, а затем эту вторую точку - с некоторой третьей, третью – с четвертой и т.д., то в этом случае говорят, что отрезки последовательно соединяют данные точки. После этого учащимся предлагается по аналогии с определением треугольника перечислить признаки, которыми должен обладать четырехугольник. При необходимости вносятся уточнения в ответы учащихся. Выясняется, что четырехугольник - это фигура, которая удовлетворяет следующим условиям:
Состоит из четырех точек и четырех отрезков;
Никакие три из этих точек не лежат на одной прямой;
Отрезки последовательно соединяют данные точки;
Эти отрезки не пересекаются;
Составляется определение четырехугольника, которое рекомендуется записать в тетрадь.
Использование таких путей руководства творческой деятельностью учащихся повышает интерес к изучаемому материалу и создает условия, благоприятные для воспитания творческой активности и самостоятельности учащихся
В процессе обучения учитель руководствуется принципами:
формирование и развитие у школьников внутренних мотивов к обучению математике;
практическая направленность обучения, формирование умений решать учебные задачи;
формирование творческого подхода к решению задач;
учет достигнутого уровня обученности и развитости;
планирование конечного результата;
учет психолого-педагогических закономірностей (замечать и поощрять малейшие успехи детей, не подвергать осуждению, критике их неудачи и промахи).
Руководствуясь данными принципами, учитель выделяет следующие задачи обучения математике:
Формирование у школьников базового фонда предметных знаний и умений.
Формирование у школьников устойчивых мотивов к учению.
Развитие творческих способностей через предмет.
Интеллектуальное развитие школьников, обучение школьников основным приемам умственной деятельности.
Нравственное воспитание учащихся через предмет.
Каждый год учитель начинает свою работу с анализа умственного развития учеников. Для этого учитель разговаривает с предыдущими наставниками детей, посещает уроки по другим предметам, пытается выяснить на каком уровне находятся их мыслительные способности, насколько сформированы навыки математических операций, понятийное и рефлексивное мышление.
После этого учитель ставит перед собой принципиальные задачи:
Освоение учащимися способов и приемов репродуктивной деятельности, которые при этом в процессе психического и интеллектуального развития личности ребенка должны им индивидуальным образом сворачиваться и становиться: во-первых, ядром различных видов продуктивной деятельности того же типа (решение примеров, уравнений, задач); во-вторых, психологическим механизмом (базой) формирования более поздних способов мыслительной деятельности.
Освоение учащимися приемов и способов аналогии, анализа, синтеза, обобщения, индуктивного умозаключения, исходя из наглядного, опытного освоения фактов.
Для решения первой задачи берется обычный материал из учебника математики 5 и 6 классов, куда входят: оперирование с положительными, отрицательными и дробными числами (десятичными и обыкновенными дробями), алгебраическими выражениями, решение уравнений с одним неизвестным и задач на составление уравнений, а также элементов геометрии. Проверка этого этапа освоения способов оперирования знаниями и навыками в стандартных условиях осуществляется через регулярную проверку домашних работ, самостоятельные и контрольные работы и диктанты.
Для реализации второй задачи проводятся тренинги, определяющие его как процесс повторения, который дает возможность по-новому посмотреть на уже воспринятый материал, и как процесс для решения стандартных операций, но включенных в новую деятельность решения принципиально новых задач.
О развитии творческих способностей учащихся с применением интерактивного обучения
Учитель считает необходимым использовать все возможности для того, чтобы дети учились с интересом, чтобы большинство из них испытали и осознали притягательные стороны математики, ее возможности в совершенствовании умственных способностей, в преодолении трудностей обучения математике. Поэтому достаточно эффективным является применение нетрадиционных форм проведения уроков или вненсения в урок нетрадиционных элементов, и каждая из них решает свои образовательные, развивающие, воспитательные задачи. Многие нетрадиционные уроки по объему и содержанию рассматриваемого на них материала нередко выходят за рамки школьной программы и предполагают творческий подход со стороны учителя и учащихся. Немаловажно, что все участники нетрадиционного урока имеют равные права и возможности принять в нем самое активное участие, проявить собственную инициативу.
Для учащихся нетрадиционный урок – переход в иное психологическое состояние, это другой стиль общения, положительные эмоции, ощущение себя в новом качестве (а значит, новые обязанности и ответственность); такой урок – это возможность развивать свои творческие способности и личностные качества, оценить роль знаний и увидеть их применение на практике, ощутить взаимосвязь разных наук; это самостоятельность и совсем другое отношение к своему труду.
Для учителя нетрадиционный урок, с одной стороны, - возможность лучше узнать и понять учеников, оценить их индивидуальные особенности, решить внутриклассные проблемы (например, общения); с другой стороны, это возможность для самореализации, творческого подхода к работе, осуществления собственных идей.
Развитие творчества у школьников напрямую связано с реализацией интерактивного обучения, поскольку интерактивное обучение обладает большими потенциальными возможностями для выполнения социального заказа современного общества.
Основой реализации интерактивных подходов к содержанию обучения является разработка и использование интерактивных заданий и упражнений, которые будут выполняться учащимися. Основное отличие интерактивных упражнений и заданий от обычных в том, что они направлены не только и не столько на закрепление уже изученного материала, сколько на изучение нового.
В настоящее время существует множество видов интерактивных заданий, но каждый из видов содержит в той или иной мере элемент творчества. Именно поэтому каждое интерактивное задание – это творческое учебное задание, которое требует от учащихся не простого воспроизводства информации, а содержит больший или меньший элемент неизвестности и имеет, как правило, несколько подходов. Кроме того, это задание должно быть практическим и полезным для учащихся; связано сих жизнью, должно вызывать интерес у учащихся и максимально служит целям обучения.
Творческое задание – основа любого интерактивного метода обучения, т.к. интерактивные методы — это методы, предполагающие усиленное педагогическое взаимодействие, взаимовлияние всех участников педагогического процесса. Суть различий пассивных, активных и интерактивных методов в форме взаимодействия учителя и обучающихся.
Например, при организации работы с теоретическим материалом в 5 классе я использую методический прием «составление закладок».
Закладка – листок бумаги шириной 4-5 см и длиной чуть больше страницы учебника (например, формата А4), который кладется справа от текста страницы и на которой ребенок в зависимости от задания помечает то, на что он обратил внимание.
Основная дидактическая цель составления закладок – создание условий для формирования навыков осознанного чтения математических текстов (такой способ работы с текстом чаще всего используется в качестве домашнего задания как способ организации предваряющего чтения).
Учащиеся получают задание одного из видов:
прочитать учебный текст и выбирать наиболее важные с точки зрения математического содержания предложения и абзацы (фрагменты текста);
выбранные фрагменты в краткой форме зафиксировать на закладке именно в том месте, где они встретились в тексте. прочитать учебный текст и разделить его на смысловые части; горизонтальными линиями указать начало и конец той или иной смысловой части; к каждой части предлагается придумать заголовок или поставить вопрос. |
|
На уроке осуществляется обсуждение результатов в группе (или с соседом по парте), поиск ответов на составленные учащимися и поставленные друг другу вопросы и т.п. Элемент творчества проявляется в оформлении закладок, в образности или точности и лаконичности комментариев к тексту.
В методе основным является характер заданий, а форма организации деятельности лишь определяет внешнее проявление общения, возможность группового, коллективного обсуждения полученного продукта, сформулированной мысли, доказательства своей точки зрения.
В зависимости от охвата обучающихся, интерактивные технологии обучения делятся на следующие формы организации деятельности:
парами (работа обучающегося в паре с обучающимся, учителем и т.д.);
фронтальная (учитель обучает одновременно группу учащихся или весь класс);
групповая или кооперативная (все учащиеся активно обучают один другого);
индивидуальная (самостоятельная работа учащихся).
Анализируя организацию работы на таком уроке, ученые пришли к выводу, что коэффициент работы учеников на отдельных уроках составляет 40-60%. Поэтому учителя, стараясь овладеть новыми педагогическими приемами, обратились к групповой форме работы, а учены е начали разрабатывать рекомендации для внедрения в практику активных методов обучения.

О развитии творческих способностей на факультативных занятиях
Факультативные занятия – форма учебной работы, состоящая в развитии способностей и интересов учащихся в сочетании с общеобразовательной подготовкой; зарождении интереса к математике на первичном уровне.
Целью организации факультативных занятий является расширение кругозора учащихся, развитие математического мышления, формирование активного познавательного интереса к предмету, привитие школьникам интереса к самостоятельным занятиям, воспитание и развитие инициативы и творчества, воспитание мировоззрения и ряда личностных качеств средствами углублённого изучения математики.
Основная задача факультативных занятий: учитывая интересы и склонности учащихся, расширить и углубить знания по предмету, обеспечить усвоение ими программного материала, ознакомить школьников с некоторыми общими идеями современной математики, раскрыть приложения математики на практике.
Факультативные курсы должны включать в себя самостоятельные исследования – упражнения, перед которыми ставится задача «открытия» незнакомого учащимся факта или способа действия. При этом учащиеся должны наблюдать, сравнивать, выдвигать гипотезы и проверять их. Огромно значение эмоционального фактора как в творчестве ученого, изобретателя, так и в творческой познавательной деятельности учащегося. Именно интерес к изучаемому материалу может побудить учащихся к активной фантазии и положительному отношению к изучаемому материалу. Учитель, который создает такие условия обучения, при которых учащиеся открывают для себя усваиваемые знания и действия, может с полным правом сказать, что он не только сообщает ученикам знания, но и развивает их творческие способности.
Факультативные занятия играют большую роль в совершенствовании школьного, в том числе математического образования. Они позволяют производить поиск и экспериментальную проверку нового содержания, новых методов обучения, в широких пределах варьировать объём сложности изучаемого материала. Примечательной особенностью факультативного курса является то, что программа курса для каждого класса составлена из ряда основных тем, содержание которых непосредственно примыкает к общему курсу математики. Однако содержание учебной работы учащихся на факультативных занятиях определяется не только математическим содержанием изучаемых тем и разделов, но и различными методическими факторами:
характером объяснения учителя;
соотношением теории и учебных упражнений;
содержанием познавательных вопросов и задач; сочетанием самостоятельной работы и коллективного обсуждения полученных каждым учащимся результатов.
При выборе методов и приёмов обучения на факультативных занятиях необходимо учитывать содержание факультативного курса, уровень развития и подготовленности учащихся, их интерес к тем или иным разделам программы. Одним из важнейших требований к методам является активизация мышления учащихся, развитие самостоятельности в различных формах её проявления. На факультативных занятиях могут использоваться разнообразные формы проведения занятий: лекции, практические работы, обсуждение заданий по дополнительной литературе, доклады учеников, составление рефератов, экскурсии. На практических занятиях проводится целенаправленная работа по выработке у учащихся умений и навыков решения основных типов задач. Полезная форма работы - подготовка рефератов. Выполнение таких заданий важно прежде всего в отношении развития навыков самообразования, удовлетворение индивидуальных интересов учеников. Одновременно индивидуальное задание должно иметь ценность для всех участников факультативной группы.Очень большое значение для успешности усвоения материала имеет подбор задач.
Хотелось ещё отметить, что факультативные занятия должны быть интересными, увлекательными. Хорошо известно, что занимательность изложения помогает раскрытию содержания сложных научных понятий и проблем. Занимательность поможет школьникам освоить факультативный курс, содержащиеся в нём идеи и методы математической науки, логику и приёмы творческой деятельности. В этом отношении цель учителя – добиться понимания учениками того, что они подготовлены к работе над сложными проблемами, но для этого необходима заинтересованность предметом, трудолюбие, владение навыками организации своей работы.
ПРИМЕНЕНИЕ ТЕОРЕТИЧЕСКИХ НАРАБОТОК В ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ УЧИТЕЛЯ
Если на уроке хоть 5 минут я трачу на элементы творчества, то ощущаю, что уже это приносит свои плоды. Какие же элементы творчества можно внести в урок математики? Это могут быть задания, которые требуют творческого отношения к работе, своего личного суждения, мнения, отношения, позволяющего делать выводы:
составление тестов;
составление кроссвордов, ребусов, чайнвордов на основные понятия;
составление опорных конспектов;
составление плана ответа на доказательство теоремы;
нахождение оригинального способа решения задачи;
составление задачи, используя данные;
нахождение ошибок, допущенных в формулировке задания;
В зависимости от возраста, уровня развития и уровня подготовки класса можно предложить детям задачи на смекалку, задачи-шутки, задачи с геометрическим содержанием, задачи на раскрашивание, логические упражнения со словами, игры, фокусы, шарады. Время проведения таких «разминок» - около 10минут. А проверить выполнение задания можно путем самопроверки или взаимопроверки. Задания даются всему классу. При их выполнении оценивать следует только успех.
Приведу пример диктанта, в который включены вопросы не только математического содержания. Такого рода диктант стимулирует мыслительную деятельность учащихся, дает возможность сосредоточиться. Его можно провести как в начале урока в качестве небольшой разминки, так и в конце, чтобы «взбодрить» уставших учеников.
Какое сегодня число?
Какой день недели по счету был вчера?
Части 8 и 2. Найди целое.
У стола 4 угла. 2 угла отпилили. Сколько осталось?
Какое время суток сейчас?
Какая буква вторая в слове «воробей»?
15 уменьши на 6. Запиши ответ.
Сколько дней в неделе?
На уроке не удается давать много творческих задании, а использовать занимательность на самых разных его этапах представляется возможным. Это могут быть:
занимательные задания на повторение учебного материала;
занимательные задания для осознания, осмысления нового учебного материала;
занимательные задания на формирование алгоритма действий, умений;
занимательные задания для творческой самостоятельной работы;
занимательные задания в игровой форме;
занимательные задания повышенного уровня сложности и трудности.
Приведу некоторые примеры использования занимательных заданий
1) Расшифруйте фамилию математика, который впервые использовал термин функция. Для этого в квадратиках впишите букву, соответствующую графику заданной функции. В оставшийся квадратик впишите букву Ц. Дополните чертеж графиком соответствующей функции.
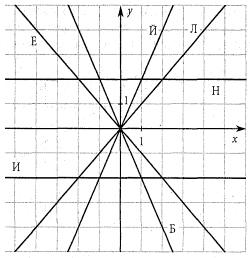

2) Расшифруйте имя греческого математика который, широко использовал правила умножения и деления положительных и отрицательных чисел. Для этого выполните умножение. Выберите буквы, соответствующие найденным ответам, и запишите в таблицу. Свободный столбец заполните, учитывая результат
Т3,4 · (0,5) =
Ф 2,7· (10) =
Н-4 · 4,2 =
И 6,2 · (-5) =
Е-2,5 · 0,4 =
Д
О-24,8 · 
 =
=
А
| -40 | -31 | 12,4 | -27 | -0,5 | -16,8 |
| | | | | | |
В устной работе на уроке, выполняя задания с историческими фактами развития математики, учащиеся пополняют свои знания фактами, справками из истории математики и жизни ученых математиков, при этом происходит развитие интереса к математике как науке и как к предмету. Такие занимательные задания могут иметь продолжение при написании рефератов о жизни ученых математиков, об открытии тех или иных фактов науки математики.
3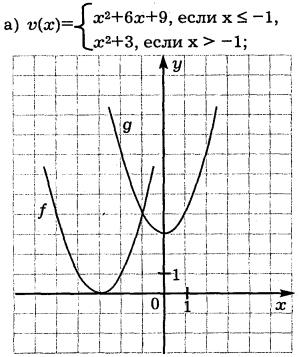 ) Используя данные графики а) и б), создайте (обведите цветным карандашом) графики заданных формулами функций.
) Используя данные графики а) и б), создайте (обведите цветным карандашом) графики заданных формулами функций.
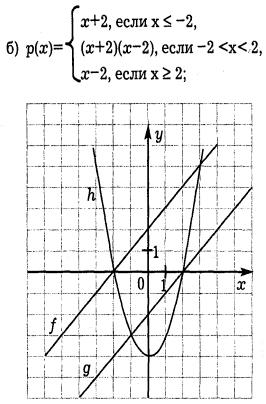
1) Зачеркните все пары противоположных чисел и соответствующие им буквы. Оставшиеся буквы позволят вам прочитать, как раньше назывались положительные и отрицательные числа.
| 1 | 5 | 5,4 | 3 | -5 | 2,5 | 1,5 | -0,75 | -5 | 8 | -1 | 
|
| Д | С | М | О | К | Л | А | У | С | Г | Т | Ж |
| -0,25 | 5 | 8 | 
| 
| 1,25 | 64 | -1 | -32 | -65 | 6 | 32 | 1 | 1 | 0,6 |
| Р | И | М | Ф | У | З | Щ | А | Ю | Е | С | Б | Т | В | О |
2) Знаете ли вы, какие открытия и изобретения были сделаны Декартом? Заполните таблицу координатами точек, используя данный чертеж.
3) При повторении противоположных чисел, при изучении координатной плоскости можно предложить задание, с исторической справкой. Замечено, что после чтения или рассказа без деятельности самих учащихся исторические факты стираются из памяти гораздо быстрее либо не запоминаются совсем, нежели когда учащиеся получают данные сведения в ходе выполнения конкретного задания. Занимательные задачи могут быть связаны с любыми интересными фактами.
Задача. Однажды ученые нашли в Индии древнюю математическую рукопись. Их заинтересовала одна запись:
Впоследствии выяснилось, что индийцы-математики так записывали пропорцию. Запишите ее в современном виде и проверьте, верна ли она.
4) В восточных странах Китае, Корее, Вьетнаме, Японии и других люди едят при помощи палочек. Часто их делают из бамбука, древесины, слоновой кости и металла. В Китае такие палочки называются “Куайцзы”.
Узнайте, как палочки для еды называются в Японии. Для этого выполните задания, учитывая, что (а) - арифметическая прогрессия. Зачеркните в таблице буквы, соответствующие найденным ответам.
а1=20, d = 4.Найдите а 5а5 = ...
а1= 1,7, d = -0,2.Найдите а 8 а8 = ....
- 8; - 6,5; ...Найдите а 4а 4 =…
а1=- 14,5, a10= 0,2. Найдите dd =...
| -3,5 | 3,5 | 36 | 0,3 | 33 | -2,5 | 2,5 | 0,7 |
| Г | Х | У | Ф | А | С | Е | И |
5)Заполните ячейки квадрата
6) Заполните четвертый квадрат.





![]()
![]()




![]()


![]()
![]()
![]()
![]()
![]()






7) Расставьте в пустые клетки недостающие цифры так, чтобы их сумма по всем направлениям была равна девяти (цифры могут повторяться)
Занимательные задания на формирование умений применять алгоритм действий, закрепление знаний.
1) Упражнение “Стрела”. Найдите сумму выражений 5х - 3у и -2х + у и результат запишите в третью клетку. Найдите сумму двух последних выражений и запишите результат в следующую клетку и т.д. Какое выражение будет записано в 7-й клетке?
3) Упражнение “Простая ромашка”.
а) Запишите простые числа в лепестках ромашки так, чтобы произведение всех чисел равнялось 120.
б) Нарисуйте “простую ромашку” для числа 136. Сколько у нее будет лепестков?
в) Можно ли нарисовать “простую ромашку” для числа 67? Обоснуйте свой ответ.
г) Выберите какое-нибудь свое число, нарисуйте для него “простую ромашку”, если это возможно.
В ходе урока это задание можно обыграть. Этапы а), б), в) можно использовать как небольшое соревнование. В зависимости от целей урока упражнение “Простая ромашка” можно использовать для повторения, для закрепления умений использовать алгоритм разложения числа на простые множители.
1) Задание с продолжением.
а) Запишите функцию, графиком которой является парабола,
б) и ее ветви опущены вниз,
в) и она проходит через точку (-1; -8).
2) Постройте график квадратичной функции, если известно, что он проходит через точки (-4; -4), (-2; -3), (0; 4).
3) Придумайте задачу о прямоугольнике, решение которой приводит к системе уравнений
4) У школьников спрашивают: «Как, пользуясь тремя карточками с цифрами 9, 2, 9 и используя два математических знака «+» изобразить сумму 20?
9
+
2
+
9
5)По какому признаку можно объединить следующие числа:
121, 40, 31, 22 ?
2, 9, 20 ?
1, 5, 7 ?
6)Проанализируйте следующие ряды чисел, выявите закономерность и продолжите их запись:
1, 3, 4, 7, 11, 18…
2, 8, 3, 7, 4, 6…
7) Найдите принцип, по которому расставлены числа, и вставьте пропущенное: 4 8 6 9 4 1
6 2 4 6 6 2
8 6 ? 1 9 ?
Задание «Найди ошибку»: втакого рода заданиях можно ввести какого-либо математического героя. При рассмотрерии ситуаций, в которые попадает указанный герой, у учащихся формируются такие качества, как внимательность .осознанность в поиске решения, умении решать задачу несколькими способами, выбирать рациональное решение
1) В теме “Решение линейных уравнений” найди ошибку в решении уравнения
2- (Зх + 7) - 3 = 17;
6х + 14 - 3 = 17;
6х = 17 - 3 - 14;
6х = 0;
х = 0.
2) Верно ли Витя Верхоглядкин выделил квадрат двучлена в каждом случае:
а) х2+ 8 х - 10 = (х + 4)2 + 16 - 10 = (х + 4)2 + 6,
б) х2-2х = (х-2)2 + 4?
3) Функция задана формулой у = 2 х + 7. Найдите значение функции при значении аргумента, равного 1; - 20; 43.
Занимательная форма задания (игровой момент).
Ученик вызывается к доске, ему выдается карточка, на которой записана формула функции у = 2х + 7. Учащимся класса эта формула неизвестна. Требуется эту формулу определить в процессе работы: учащиеся поочередно задают значения х, а ученик у доски по этим значениям находит каждый раз значения функции по заданной формуле и заполняет таблицу, которая есть на доске.
4)Используя шрифт, узнайте название кривой
1) В теме “Признаки делимости” на 4 делятся числа, которые оканчиваются двумя нулями или у которых две последние цифры составляют число, делящееся на 4.
1935212 делится нацело на 4, так как две последние цифры составляют 12.
Ответьте на вопросы:
а) Делятся ли на 4 следующие числа и почему: 135668, 109845876, 257000, 50000055014?
б) Будут ли делиться на 4 числа, если вместо * поставить любые цифры **32, ** 76, **24, **30, **51, **20?
в) Придумайте многозначные числа, которые будут делиться на 4.
2) В теме “Одночлены и многочлены” разложите на множители многочлен 35а2 - 21ab + 30ас - 18с.
а) Если изменить знак каждого коэффициента на противоположный, получится многочлен
- 35а2 + 21ab –30ас + 18хс. Можно ли его разложить на множители?
б) Если изменить все знаки, кроме одного. Можно ли его разложить на множители?
в) Если изменить только два знака. Можно ли разложить этот многочлен на множители?
Таким образом, занимательные задания разных типов позволяют эмоционально представить учебный материал, сделать деятельность учащихся на уроке творческой. Нередко занимательно сформулированная учителем проблема направляет учащихся на самостоятельный поиск решения, самостоятельное выдвижение новых математических идей.
Инструментом для развития творческого мышления, творческого воображения, которые ведут к формированию творческой деятельности школьника, являются задачи "на соображение", "на догадку", головоломки, нестандартные задачи, логические задачи, творческие задачи. Их можно успешно использовать на уроках в качестве дополнительного пути для формирования элементов творческой деятельности. Для решения заданий характере процесс поисковых проб, появляется догадка, которая свидетельствует о развитии у школьников качеств умственной деятельности, как смекалка и сообразительность. Поэтому целесообразным считаю применение заданий для развития умений выделять существенное, сравнивать и обобщать.
Задание №1.
Прочитай. Выбери задание, которое не относится к теме. "Нахождение периметра".
Измерь стороны прямоугольника.
Измерь длину ломаной, изображенной на рисунке.

Найди сумму длин сторон прямоугольника.
Объясни, почему выбранное задание лишнее.
Задание №2.
Распредели задания на две группы.
Начерти тупой угол.
Начерти угол, который не является ни острым, ни тупым.
Начерти угол больше прямого.
Начерти угол, который образуют верхняя и правая стороны твоего листа.
Докажи правильность своего распределения.
Задание №3.
Установи соответствия. Соедини линией геометрическую фигуру и ее название.
Т очка
очка
П
 рямоугольник
рямоугольник
К

 руг
руг
П рямая
рямая
Квадрат
О трезок
трезок
Задание №4
Нарисовать картину с помощью 20 геометрических фигур: 4 больших и 4 малых квадрата, 3 больших и 3 малых треугольника, 2 больших и 2 малых круга, 1 большой и 1 малый прямоугольник, лист основы (формат А4), клей. Цвет фигур – произвольный. Задание выполняется в три этапа: 1) создание картины; 2) подбор названия и составление рассказа по картине; 3) описание хода работы по созданию картины.
К заданиям креативного типа относятся задания: создать словесный портрет в различных жанрах, сочинить сказку, составить кроссворд, игру, сценарий праздника, оживить число, придумать образ – рисуночный, двигательный, музыкальный.
Выбор сочетания форм при выполнении творческих заданий зависит от целей выполнения этих заданий и уровня сложности. В процессе выполнения этих заданий создается атмосфера творчества. Ребята более глубоко проникают в изучение предмета, понимают значимость и величие науки. Обучающиеся сами создают творческие задания, которые отличаются разработанностью и оригинальностью. Это исследовательские работы, рефераты, сказки, шарады, головоломки, кроссворды. Уроки становятся интересными, насыщенными и увлекательными. Учащиеся ждут с интересом нового.
ЗАКЛЮЧЕНИЕ
На основе разносторонней характеристики возрастных и индивидуальных особенностей развития творчества школьников творчество рассматривается как познавательная деятельность, направленная на усвоение учащимися знаний, выработанных человечеством в ходе общественного развития. Овладение знаниями рассматриваются как активный процесс углубления в сущность изучаемых явлений, в раскрытии их свойств, связей и отношений. Этот процесс требует овладения способами действий, аналитико-синтетическими операциями, характер которых определяется содержанием той области знаний, на усвоение которой они направлены.
Если рассматривать творчество с точки зрения новизны и оригинальности решаемых задач, то можно выделить творчество творческое (продуктивное) и воспроизводящее (репродуктивное). Творчество направлено на создание новых идей, его результатом является открытие нового или усовершенствование решения той или иной задачи. В ходе творчества возникают новообразования, касающиеся мотивации, целей, оценок, смыслов внутри самой познавательной деятельности. Необходимо отличать создание объективно нового, то есть того, что еще никем не было сделано, и субъективно нового, то есть нового для данного конкретного человека. В качестве препятствий развитию творчества может выступать излишняя критичность, внутренняя цензура, желание найти ответ немедленно, стремление пользоваться старыми знаниями, боязнь выделиться и стать смешным для окружающих.
Формирование творчества на уроках математики, через решение определенного типа задач, в форме увлекательных игр, обогащает педагогический процесс, делает его более содержательным, влияет на развитие ребенка, как на творческую личность.
ЛИТЕРАТУРА
Развитие творческой активности школьника.
Под ред. А.Н. Матюшкина. М., Педагогика, 2003 г
Учим творчески мыслить на уроках математики. Шуба М.Ю. М., Просвещение, 2012г.
Дидактические игры на уроках математики. В.Г.Коваленко. М., Просвещение, 1990г.
Воспроизводящая и творческая деятельность учащихся в обучении.
Под ред. И.Т.Огородникова М., 2002 г.
Проблемные ситуации в мышлении и обучении. Матюшкин А.М. М., 2003 г.
Развитие творческих способностей учащихся на факультативных занятиях по математике, Н.Н.Иванова
Как реализовать компетентностный подход на уроке и во внеурочной деятельности. М., «Аркти», 2009 г.
Математическая шкатулка. Ф.Ф.Нагибин.
Интернет ресурсы


























 ) Используя данные графики а) и б), создайте (обведите цветным карандашом) графики заданных формулами функций.
) Используя данные графики а) и б), создайте (обведите цветным карандашом) графики заданных формулами функций.










