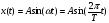Тема урока:
Моделирование в среде табличного процессора. Величины, характеризующие колебательное движение.
Цели урока по физике:
Ввести понятия амплитуды, периода и частоты колебаний; сформировать представление о гармонических колебаниях.
Цели урока по информатике:
Сформировать и развить исследовательские навыки учащихся; освоить технологию моделирования в среде табличного процессора.
Ход урока
Проверка домашнего задания, повторение
По информатике
- Назовите два основных типа постановки задач моделирования. (Что будет, если? и Как сделать, чтобы?)
- Назовите основные этапы моделирования
- По каким причинам компьютер широко используется в моделировании?
- Назовите известные вам инструменты компьютерного моделирования.
- Что такое компьютерный эксперимент? Приведите пример.
- Что такое тестирование модели?
- Какие ошибки встречаются в процессе моделирования? Что надо делать, когда ошибка обнаружена?
- В чем заключается анализ результатов моделирования?
По физике
Приведите примеры колебательных движений.
Как вы понимаете утверждение о том, что колебательное движение периодично?
Что такое период колебаний?
Какие колебания называются свободными?
Что такое смещение, амплитуда?
Что такое колебательные системы?
Что называется маятником?
Какие тела входят в колебательную систему, называемую пружинным маятником? Нитяным (математическим) маятником?
II. Новый материал
Информатик
Ни у кого не вызывает сомнений, что электронные таблицы являются наиболее подходящей средой для моделирования. Мы уже использовали их для выполнения численных расчетов и быстрого пересчета значений при изменении исходных данных на примере задачи о склеивании коробки. Табличный процессор предоставляет более удобную среду для выполнения таких расчетов, чем среда программирования.
Особенности постановки задач и их вычислительная направленность позволяют провести в среде табличного процессора полномасштабный компьютерный эксперимент
Сегодня на уроке основу выполнения расчетов будет составлять математическая модель, представленная физической формулой, связывающей параметры моделируемых объектов. На этапе разработки математическая модель преобразуется в компьютерную.
Физик
Каждое движение характеризуется своими величинами.
Какими величинами характеризуется равномерное прямолинейное движение? (Постоянной скоростью, координатой. Существует уравнение зависимости координаты от времени х = х0 + vxt.)
Какими величинами характеризуется прямолинейное движение? (Постоянным ускорением, координатой.)
Какими же величинами характеризуется колебательное движение?
Период колебаний
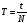 На прошлом уроке уже отмечалось, что колебательное движение - периодическое. Период Т- время одного полного колебания:
На прошлом уроке уже отмечалось, что колебательное движение - периодическое. Период Т- время одного полного колебания:
где t - все время движения, N- количество колебаний.
В СИ период колебаний выражается в секундах: [T] = с.
Частота колебаний
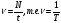 Частота v - число полных колебаний за единицу времени:
Частота v - число полных колебаний за единицу времени:
где N- количество колебаний, t - время движения. В СИ частота выражается в герцах: [v] = с-1 = Гц. Колебательное движение характеризуются также циклической частотой: 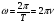
Амплитуда колебания
Амплитуда х (или А) - наибольшее смещение от положения равновесия, измеряется в метрах (м). Можно измерять в единицах плоского угла (для математического маятника).
Графическое представление колебательного движения
Так как в процессе колебаний положение тела меняется, то очень удобно изменение смещения тела от положения равновесия во времени представлять графически. Подготовив установку, предложенную, в учебнике на стр. 97, демонстрируем вид траектории движения. Полученная кривая называется синусоидой.
Периодические изменения во времени физической величины происходящие по закону синуса или косинуса, называются гармоническими колебаниями.
Закон изменения смещения х от времени t имеет вид:
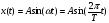
Рассмотрим на конкретной задаче график зависимости смещения х от времени и определим амплитуду, период и частоту колебаний.
Информатик
Для этого построим компьютерную модель в среде табличного процессора.
I этап: Постановка задачи Описание задачи
Нам необходимо решить физическую задачу:
Координата колеблющегося тела изменяется по закону: х(t) = 0,1sin(2,5pt)Чему равны амплитуда, период и частота колебаний, если в формуле все величины выражены в единицах СИ?
Цели моделирования
Определить амплитуду, период и частоту колебаний.
Построить график функции.
Формализация задачи
Формализация задачи проводится в виде поиска ответов на вопросы:
| Вопрос | Ответ |
| Что моделируется? | Колебания маятника |
| Что известно? | х(t) = 0,1sin(2,5pt) |
| Как определить максимальное смещение координаты? | Проследить, как изменяется максимальное смещение координаты при изменении времени t |
| Как изменяется время? | Увеличивается от нуля с заданным шагом |
| Какой шаг изменения времени? | Так как колебания происходят достаточно быстро, возмем шаг 0,1 с |
II этап. Разработка модели
Информационная модель
При формализации задачи мы получаем следующие объекты моделирования и их параметры:
| Объект моделирования | Параметры |
| Обозначения | Значения |
| Время | t | исходные |
| Смещение координаты | х | расчет |
По какой формуле из исходных данных получить желаемый результат.
х(t) = 0,1sin(2,5pt)
Компьютерная модель
При составлении компьютерной модели обращаем внимание на несколько моментов.
Во-первых, электронная таблица для решения задачи должна включать две области: исходные данные; результаты.
Во-вторых, таблица должна включать различную пояснительную ин-формацию: название задачи, названия областей и параметров и т. д.
В-третьих, очень большое значение имеет правильное использование относительных и абсолютных ссылок.


Физик
- Определим по графику амплитуду колебаний, период и частоту.(А=0,1м, Т=0,8с, n=0,25 Гц)
- Где будет находиться маятник через 2с после начала колебаний?(В начальном положении (отвесном).
Информатик
III этап. Компьютерный эксперимент План эксперимента
Тестирование: провести тестовый расчет компьютерной модели.
Эксперимент 1: проследить, как с уменьшением амплитуды в формуле изменится график колебаний.
Эксперимент 2: проследить, как с увеличением амплитуды в формуле изменится график колебаний
Эксперимент 3: проследить, как с увеличением периода в формуле изменится график колебаний.
Эксперимент 4: проследить, как с уменьшением периода в формуле изменится график колебаний.
Закрепление
Задача 1
Координата колеблющегося тела изменяется по закону: х = 5 cos л t. Чему равны амплитуда, период и частота колебаний, если в формуле все величины выражены в единицах СИ? (Ответ: А = 5м; Г= 2 с; v = 0,5 Гц.)
Задача 2
Математический маятник длиной 2,45 м совершил 100 колебаний за 314 с. Определить ускорение свободного падения для данной местности. (Ответ:
g = 9,8 м/с2.)
Задача 3
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с2. (Ответ: / = 0,16 м.)
Домашнее задание
по информатике:
Устно: стр. 153, вопросы 1-12.
по физике:
Выучить §26, 27;







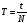 На прошлом уроке уже отмечалось, что колебательное движение - периодическое. Период Т- время одного полного колебания:
На прошлом уроке уже отмечалось, что колебательное движение - периодическое. Период Т- время одного полного колебания: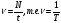 Частота v - число полных колебаний за единицу времени:
Частота v - число полных колебаний за единицу времени: