Реализация межпредметных связей для развития познавательных УУД обучающихся на уроках математики

Реализация межпредметных связей для развития познавательных УУД обучающихся на уроках математики

Вряд ли кто-либо в настоящее время станет отрицать тот факт, что стремительные изменения в обществе требуют от человека абсолютно новых качеств личности. В изменившемся мире ценными становятся не только знания, но и умения, связанные с их поиском, интерпретацией, использованием.

По своей сути, образовательный процесс должен быть ориентирован на формирование, освоение и развитие способов деятельности — универсальных учебных действий.

Медведева Алла Юрьевна

учитель математики

МКОУ С(К)ШИ № 116

Основные ориентиры развития учебно-познавательной деятельности

Уровни образования

Ориентир

Начальное общее образование

Умение учиться

Основное общее образование

Умение учиться сообща

Среднее общее образование

Умение учиться самостоятельно

Логика системы универсальных учебных действий в начальном общем, основном общем и среднем (полном) общем образовании напрямую связана с основными ориентирами развития учебно-познавательной деятельности по уровням образования. Она раскрывается следующим образом (см. табл.).

Функции универсальных учебных действий

№

Функция универсальных учебных действий

1

Ключевая характеристика

Обеспечение возможностей обучающегося самостоятельно осуществлять деятельность учения, ставить учебные цели, искать и использовать необходимые средства и способы их достижения, контролировать и оценивать процесс и результаты деятельности

2

3

Создание условий для гармоничного развития личности и ее самореализации на основе готовности к непрерывному образованию, необходимость которого обусловлена поликультурностью общества и высокой профессиональной мобильности

Самостоятельность обучения

Самореализация

Обеспечение успешного усвоения знаний, умений и навыков и формирование компетентностей в любой предметной области

Успешность в освоении знаний

Наиболее полно понятие «универсальные учебные действия» рассматривается в одном из базовых документов системы Федеральных государственных образовательных стандартов — Фундаментальном ядре содержания общего образования.

Там же перечислены функции универсальных учебных действий (то есть то, для чего они нужны). Первая из них связана с тем, чтобы обеспечить обучающемуся возможность самостоятельно учиться, вторая — с созданием условий для самореализации ученика, а третья — с созданием ситуации успеха в освоении знаний.

коммуникативные

познавательные

• учебное сотрудничество
• действия разрешения конфликтов
• умение с достаточной полнотой и точностью выражать свои мысли

• общеучебные универсальные действия 
• логические универсальные действия 
• постановка и решение проблемы

личностные

регулятивные

• действия самоопределения
• действия смыслообразования
• действия нравственно- этического оценивания

• действия целеполагания
• действия планирования
• составление плана и последовательности действий
• действия контроля
• Коррекция
• действия оценки
• волевой саморегуляции

Фундаментальное ядро содержания общего образования определяет четыре группы универсальных учебных действий: личностные предполагают, прежде всего, личностное развитие обучающегося, регулятивные — организационные умения (в том числе и саморегуляцию), познавательные УУД — общеучебные умения, а коммуникативные — речевое развитие и социальную адаптацию.

Таким образом, задача формирования универсальных учебных действий, позволяющих достигать метапредметных результатов (регулятивных, коммуникативных, познавательных) приобретает особую актуальность.

И одним из способов достижения метапредметных результатов можно считать внедрение в урок различного вида заданий.

На уроках математики это могут быть: реальные задачи; задачи, содержащие исторические факты; задачи на оперирование с различными видами представления информации и перевод информации из одного вида информации в другой (таблица, текст, диаграммы, график, рисунок, схема и др.); задачи с межпредметным содержанием, практические задачи.

В классе 30 человек. Решив уравнение,

учащиеся разделились во мнениях, чему равен корень уравнения. Ответы были следующие: 7, -7 и нет корней.

На диаграмме показано количество учеников, выбравших один из ответов. Согласен ли ты с мнением большинства?

Если нет, приведи свой вариант ответа. Ответ обоснуй.

При выполнении данного задания формируется познавательное учебное действие – умение считывать информацию с диаграммы и выбирать наиболее рациональный способ решения.

1. В классе 30 человек. Решив уравнение , учащиеся разделились во мнениях, чему равен корень уравнения. Ответы были следующие: 7, -7 и нет корней.

На диаграмме показано количество учеников, выбравших один из ответов. Согласен ли ты с мнением большинства? Если нет, приведи свой вариант ответа. Ответ обоснуй.

Ответ: не согласен, число 7 не является корнем уравнения, так как при подстановке его в уравнение не получаем верное числовое равенство. Корнем уравнения является число -7, так как при подстановке его в уравнение получаем верное числовое равенство -15= - 15. *

* Еще один возможный вариант: ученик начнет сам решать уравнение и придет к верному ответу, но это уже не будет наиболее рациональным способом решения.

Арка Звезды в Париже 1806-1836 гг.

1) Выберете верную математическую модель, которую можно использовать для нахождения высоты Арки Звезды в Париже (возможно несколько верных ответов):

а) ширина арки – x метров, высота арки – (x+5) метров,

отношение ширины арки к высоте – ,

уравнение ;

б) ширина арки – x метров, высота арки – (x+5) метров,

отношение ширины арки к высоте – ,

уравнение ;

в) высота арки– x метров, ширина арки – (x – 5) метров,

отношение ширины арки к высоте – ,

уравнение ;

г) одна часть – x, ширина арки – 9x,

высота арки – 10x, уравнение 10x – 9x = 5.

2 ) На сколько метров Арка Звезды в Париже выше Арки Константина в Риме?

Ширина Арки Звезды в Париже относится к ее высоте как 9:10. Известно, что высота данной Арки на 5 м больше ее ширины. А высота Арки Константина в Риме равна 21 метру.  

При выполнении следующего задания формируется познавательное учебное действие – моделирование (перевод текстовой информации в знаково-символическую форму), анализ и синтез информации.

Арка Константина в Риме 312-315 г. н.э

К новому учебному году тебе нужно купить 24 тетради, 12 ручек и 5 простых карандашей с ластиком. Тетрадь на 2 рубля дешевле карандаша и в 2 раза дешевле ручки. Стоимость всей покупки составляет 593 рубля. Мама дала 750 рублей. Хватит ли тебе денег еще купить набор линеек, если его стоимость на 138 руб. дороже ручки?

Реши задачу, используя данный алгоритм:

1) Принять стоимость одной тетради за x;

2) Выразить стоимость одной ручки и одного карандаша через x;

3) Выразить стоимость 24 тетрадей, 12 ручек и 5 простых карандашей через x;

4) Составить уравнение на основании того, что стоимость всей покупки составила 593 рубля;

5) Решив составленное уравнение, найти стоимость одной тетради;

6) Найти стоимость одной ручки;

7) Найти стоимость набора линеек с учетом того, что он дороже одной ручки на 138 рублей;

8) Найти стоимость всей покупки с учетом набора линеек;

9) Сравнить количество имеющихся денег со стоимостью покупки с учетом набора линеек;

10) Сделать вывод, хватит ли денег на набор линеек или нет.

При выполнении третьего задания формируется регулятивное учебное действие – умение действовать по заданному алгоритму.

Систематическое использование таких задач и заданий, направленных на развитие УУД, расширяет математический кругозор школьников и позволяет более уверенно ориентироваться в закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.

Я предлагаю несколько заданий, которые, на мой взгляд, при включении в урок математики, помогут сформировать и развить у обучающихся метапредметные умения и навыки.

1 вид заданий

Главной отличительной особенностью заданий является то, что большинство имеет занимательную форму. выполнение заданий позволяет расширить кругозор обучающихся в историческом аспекте, пополнить лексический запас новыми терминами, узнать о этимологическом происхождении, получить дополнительную информацию об окружающем мире.

Наряду с формированием математических знаний, задания пособия помогают развивать у детей логическое мышление, интерес к предмету. Занимательная форма заданий привлекает детей, побуждает их к четкой, последовательной и аккуратной деятельности. Могут использоваться на всех этапах урока и во внеурочной деятельности.

Данные задачи способствуют

- развитие интереса к математическому творчеству и математических способностей;

- проявление целеустремленности, креативности, трудолюбия, дисциплинированности, ответственного отношения к учению;

- умение самостоятельно организовать собственную деятельность;

  - умение работать по алгоритму, с памятками, правилами;

-  умение самостоятельно вести поиск информации;

-умение выделять основное содержание прочитанного текста, находить ответы на поставленные вопросы и излагать его.

-умение обобщать и сравнивать результаты;

- умение использовать знаково-символьную запись математических понятий.

-приобретение опыта самостоятельного поиска;

-развитие интереса и способностей учащихся на основе передачи им знаний и опыта познавательной и творческой деятельности.

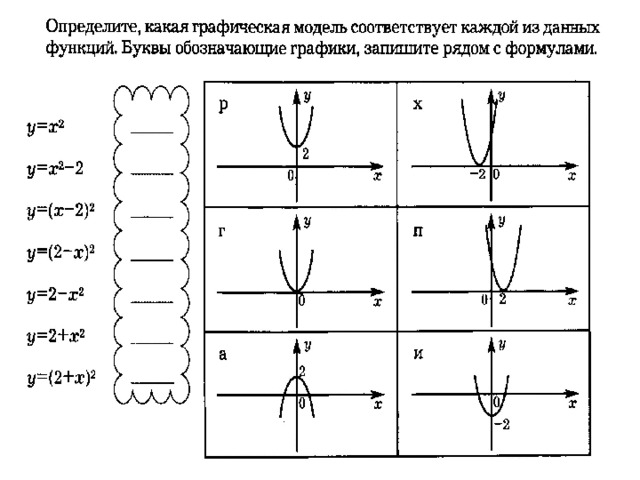
Практические задачи

2 вид задач составлен на основе проблемных ситуаций, связанных с разнообразными аспектами окружающей жизни. Для их решения наряду с математикой необходимо использовать знания, приобретенные при изучении других школьных предметов. Основным метапредметным умением, формируемым при решении таких задач, является умение моделировать, т. е. умение строить и исследовать математические модели.

Задачи расположены в порядке усложнения реальной ситуации, в которой применяется в данном случае геометрия.

Одновременно происходит и усложнение математических моделей, которые строят школьники в процессе решения задач. Задачи подкреплены иллюстрациями, что способствует лучшему пониманию сюжета задачи и позволяет сформировать у школьников математический взгляд на мир.

Прочитайте текст: Вставьте пропущенное число.

Среднее расстояние от Земли до Луны составляет 384 900 км. Почему «среднее»? Потому что Луна вращается вокруг Земли по эллиптической орбите и в какой-то момент она находится дальше, а в какой-то, наоборот, - ближе к нашей планете. Вот почему 384 900 км считается средним расстоянием до Луны или, как говорят астрономы, является «большой полуосью орбиты Луны». Когда Луна находится в самой ближайшей к Земле точке (перигее), нас разделяет всего 363 104 км. А расстояние от самой удаленной точки (апогея) до Земли – 406 696 км. Получается, что расстояние от Земли до Луны – величина непостоянная, она изменяется на ______ км. Именно благодаря этой довольно большой разнице Луна на ночном небе кажется нам разных линейных размеров. В перигее Луна выглядит для нас на 15 % больше, чем в апогее. На самом деле меняется только ее угловой размер.

Коррекционно-развивающие познавательные задания

• Элементы упражнений 7 класс
• Элементы упражнений 8 класс

Упражнения подобраны таким образом, чтобы умственные действия, совершаемые учеником, соответствовали характеру материала и, чтобы выполнение заданий способствовало формированию различных познавательных действий, особенно мыслительных.

Такой подход обеспечивает одновременное коррекционно-развивающее воздействие на внимание, память, наблюдательность, мышление и, как следствие, речевую деятельность. Создаётся возможность самостоятельной умственной деятельности при определении нового слова в сочетании с занимательно-развивающим характером предлагаемых заданий. Опыт работы с детьми позволил апробировать на практике систему коррекционно-развивающих заданий в 7-9 классах. Часть коррекционных упражнений (геометрия, 7, 8 класс) представлена в таблице 1.

Информационные ресурсы

• Универсальные учебные действия в системе ФГОС основного общего образования: понятие, классификация, примеры: практ. пособие / авт.-сост. Т. Ю. Артюгина [и др.]. — Архангельск: изд-во АО ИОО, 2014. —30 с.
• Организация интегрированных уроков с использованием ИКТ в процессе обучения математике. Кизелевич И.Е., Фоменко Е.В (науч.рук.: к.ф.-м.н., доцент Багачук А.В.) ФГБОУ ВПО «Красноярский государственный педагогический университет им. В.П. Астафьева»
• Математика 5 класс. Тетрадь 1. Задания для обучения и развития учащихся./ Лебединцева Е. А., Беленкова Е. Ю. – М.: Интеллект-Центр, 2013 – 104 с.
• Математика 5 класс. Тетрадь 2. Задания для обучения и развития учащихся./ Лебединцева Е. А., Беленкова Е. Ю. – М.: Интеллект-Центр, 2013 – 104 с.
• Математика 6 класс. Тетрадь 1. Задания для обучения и развития учащихся./ Лебединцева Е. А., Беленкова Е. Ю. – М.: Интеллект-Центр, 2013 – 160 с.
• Математика 6 класс. Тетрадь 2. Задания для обучения и развития учащихся./ Лебединцева Е. А., Беленкова Е. Ю. – М.: Интеллект-Центр, 2013 – 176 с.
• Алгебра 7 класс. Задания для обучения и развития учащихся. Учебное пособие/ Лебединцева Е. А., Беленкова Е. Ю . – М.: Интеллект-Центр, 2013 – 152 с.
• Алгебра 8 класс. Задания для обучения и развития учащихся. Учебное пособие/ Лебединцева Е. А., Беленкова Е. Ю . – М.: Интеллект-Центр, 2013 – 176 с.
• Алгебра 9 класс. Задания для обучения и развития учащихся. Учебное пособие/ Лебединцева Е. А., Беленкова Е. Ю . – М.: Интеллект-Центр, 2011 – 104 с.
• Лукичева Е.Ю., Бунтова Ю.В., Сарамуд И.А. «Метапредметные задачи для занятий математикой в 5-6 классах: методическое пособие». – СПб.: СПб АППО, 2016. – 66 с.
• Методические разработки Концур А.В. https://nsportal.ru/node/3053742
• Глазков Ю. А. Тренажер по геометрии: 7 класс. К учебнику Л. С. Атанасяна и др. «Геометрия. 7-9 классы». ФГОС (к новому учебнику)/ Ю.А.Глазков, М. В. Егупова. _ М.: Издательство «Экзамен», 2019
• Глазков Ю. А. Тренажер по геометрии: 8 класс. К учебнику Л. С. Атанасяна и др. «Геометрия. 7-9 классы». ФГОС (к новому учебнику)/ Ю.А.Глазков, М. В. Егупова. _ М.: Издательство «Экзамен», 2019