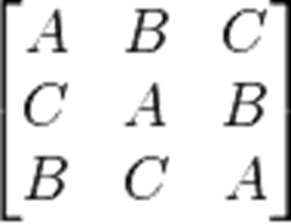Реферат на тему "Удивительный квадрат"

Министерство образования и науки

Луганской Народной Республики

ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ

«ЛУГАНСКИЙ ЛИЦЕЙ ИНОСТРАННЫХ ЯЗЫКОВ»

Кафедра естественно-математических дисциплин

Реферат на тему:

Удивительный квадрат

Учениц 8-В класса

Гончаровой Анастасии

Шикун Олеси

Научный руководитель

Богомолова Наталья Николаевна

Луганск

2017

СОДЕРЖАНИЕ

ВВЕДЕНИЕ ……………………………………………………………………………...3

РАЗДЕЛ 1. ОБЩЕЕ ПРЕДСТАВЛЕНИЕ О КВАДРАТЕ

1. Свойства квадрата ........................................................................................4

2. Исторические сведения ................................................................................4

РАЗДЕЛ 2. ПРИМЕНЕНИЕ СВОЙСТВ УДИВИТЕЛЬНОГО КВАДРАТА

2.1. Магические квадраты ………………………………………………………...5

2.2. Квадрат Пифагора …………………………………………………………….6

2.3. Квадрат в квадрате ...………………………………………………………….7

2.4. Совершенное квадрирование ………………………………………………...8

2.5. Латинские квадраты …………………………………………………………..9

2.6. Квадрат Малевича …………………………………………………………...11

РАЗДЕЛ 3. ГОЛОВОЛОМКИ

1. Задачи со спичками …………………………………………………….12

2. Оригами …………………………………………………………..…….15

ВЫВОДЫ………………………………..………………………………………………20

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ……………………………….21

ВВЕДЕНИЕ

Мы решили подготовить реферат на тему «Удивительный квадрат», так как считаем её увлекательной и познавательной. Мы изучили литературу и собрали самую интересную информацию для вас. Казалось бы, квадрат – одна из самых простых геометрических фигур. Но на самом деле и она имеет множество до сих пор, не разгаданных до конца тайн. В этом реферате были собраны все самые интересные факты о квадрате, а также его история, которая, как и сама фигура полна загадок.

Мы ставим перед собой цели: показать, насколько удивительна такая простая фигура как квадрат и показать разнообразие применения квадрата через решение различных задач.

Актуальность темы: формирование познавательного интереса к предмету математики и её истории, развитие любознательности и логического мышления. Квадрат имеет неотъемлемое значение в нашей жизни. Его используют везде и повсюду: в строительстве, в интеллектуальных играх, таких как судоку, кроссворды, крестики-нолики, морской бой и др. Тетрадь в клетку состоит из множества квадратиков. Шахматная доска имеет форму квадрата и поделена на 64 квадрата двух цветов. Квадратную форму имеет боксёрский ринг, площадка для игры в квадрат. Многие культуры называли квадрат одной из самых совершенных фигур. У римлян даже был специальный термин для гармоничного человека, по-латински, Homo quadratus, человек квадратный, человек гармоничный, построенный по высшим канонам, основанным на квадрате.

РАЗДЕЛ 1. ОБЩЕЕ ПРЕДСТАВЛЕНИЕ О КВАДРАТЕ

1. Свойства квадрата

Как всем давно известно, квадрат – это прямоугольник, у которого две смежные стороны равны или ромб, у которого все углы прямые. Перечислим основные свойства квадрата:

1. Все углы квадрата — прямые, все стороны квадрата — равны.

2. Диагонали квадрата равны и пересекаются под прямым углом.

3. Диагонали квадрата делят его углы пополам.

Укажем два практичных свойства квадрата:

1. Периметр квадрата меньше периметра любого равновеликого ему прямоугольника;

2. Площадь квадрата больше площади любого прямоугольника с тем же периметром.

1. Исторические сведения

Квадрат, как и любая геометрическая фигура, имеет свою историю. В древнем мире квадрат обычно означает четыре стороны света. И в Ассирии, и в древнем Перу четыре стороны света, четыре направления, то есть квадрат это и есть ВЕСЬ МИР. В сознании индейцев Северной Америки Вселенная – квадрат, разделенный на четыре части. Египтяне обожествляли квадрат. Греки описали его силами математики, хотя Пифагор считал все четные числа женскими и слабыми, квадрат же равно как и цифра четыре в силу их делимости и превращения ни во что были описаны лишь отрицательными характеристиками. В Исламе Кааба – пуп земли тоже кубической формы. У кельтов вселенная это три квадрата, один вложенный в другой, из центра текут четыре реки. Рассмотрим подробнее историю квадрата в других странах [https://uchiuroki.ru/teenager/interestingfact/kvadrat/].

РАЗДЕЛ 2. ПРИМЕНЕНИЕ СВОЙСТВ УДИВИТЕЛЬНОГО КВАДРАТА

1. Магические квадраты

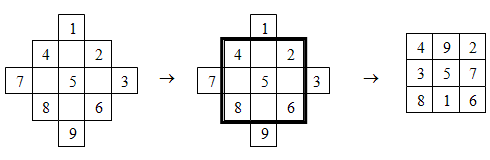
Рис. 1.2

В магическом квадрате сумма чисел в каждом вертикальном и горизонтальном рядах и по каждой из диагоналей одна и та же.

В давние времена, научившись считать и выполнять арифметические действия, люди с удивление обнаружили, что числа имеют самостоятельную жизнь, удивительную и таинственную. Складывая различные числа, располагая их друг за другом или одно под другим, они иногда получали одинаковую сумму. Наконец, разделив числа линиями так, чтобы каждое оказалось в отдельной клетке, увидели квадрат, любое из чисел которого принимало участие в двух суммах, а те, что расположены вдоль диагоналей – даже в трех, и все суммы равны между собой! Недаром древние китайцы, индусы, а вслед за ними и арабы приписывали таким конструкциям таинственные и магические свойства.

Магические квадраты появились на Древнем Востоке еще до нашей эры. Одна из сохранившихся легенд повествует о том, что когда император Ю из династии Шан (2000 г до н.э.) стоял на берегу Ло, притоке Желтой реки, вдруг появилась большая рыба (в других вариантах – огромная черепаха), у которой на спине был рисунок из двух мистических символов – черных и белых кружочков, который был осознан затем как изображение магического квадрата порядка 3.

Первое специальное упоминание о таком квадрате найдено около 1 века до н.э. Вплоть до 10 века н.э. магические квадраты были воплощены в амулетах, заклинаниях. Они использовались в качестве талисманов по всей Индии. Их рисовали на кувшинах удачи, медицинских кружках. До сих пор они используются у некоторых восточных народов как талисман. Их можно встретить на палубах больших пассажирских судов как площадку для игры.

Итак, под магическими будем понимать квадраты, в которых суммы чисел, стоящих в любом столбце или в любой строке, а также по диагоналям, одинаковы.

До сих пор вы использовали магические квадраты чаще всего для устного счета. При этом несколько чисел, в том числе и центральное, уже расставлены по клеткам квадрата. Требуется расставить остальные числа так, чтобы в любом направлении получилась определенная сумма [http://festival.1september.ru/articles/565187/].

1. Квадрат Пифагора

Квадрат Пифагора – это очень мощный аналитический инструмент. Он позволяет выявить основные особенности личности, обусловленные датой рождения. Сохранившиеся исторические источники свидетельствуют, что знаменитый математик Пифагор долго учился потаенным знаниям у египетских жрецов. У них, говорят, в племени дагонов сохранились фрагменты наук о предыдущей цивилизации. Возможно, от Атлантиды (подробнее про Атлантиду – в статье «Магия – наука древних о развитии человека«).

Пифагор в воображении художников (обратите внимание - на столе, на чертеже нарисованы Пифагоровы штаны)

Пифагор изучил в Египте, а потом привез в Европу цифровые матрицы, известные ранее только узкому кругу избранных. В адаптированном варианте тайные таблицы дошли до наших дней и ныне известны как квадрат Пифагора [http://interesko.info/kvadrat-pifagora/].

1. Квадрат в квадрате

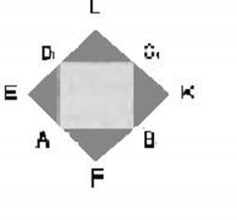
Рис. 2.2.

У квадрата, вписанного в квадрат, есть некоторые особенности. Если соединить последовательно середины сторон квадрата АВСD отрезками, то получится новый квадрат ЕFКL, площадь которого составляет половину площади данного квадрата АВСD.

Если отрезать четыре прямоугольных треугольника, расположенных по углам квадрата АВСD. Сумма их площадей также составляет половину площади квадрата АВСD. Если принять площадь квадрата АВСD за единицу, то сумма площадей отрезанных треугольников равна Ѕ.

Если в оставшийся квадрат ЕРКL таким же образом вписать квадрат A B C D и опять отрезать четыре треугольных уголка. Сумма площадей отрезанных треугольников составит Ѕ площади квадрата

ЕFKL и, значит, ј площади квадрата АВСD. Повторяя этот приём, получается еще четвёрка треугольников, сумма площадей которых составит ⅛ площади квадрата АВСD.

Применяя этот приём любое число раз, будет получаться всё новые четвёрки прямоугольных треугольников, которыми снова можно выложить первоначальный квадрат. Суммы площадей четвёрок треугольников представляют бесконечный ряд чисел.

Ѕ, ј ,⅛…

1. Совершенное квадрирование

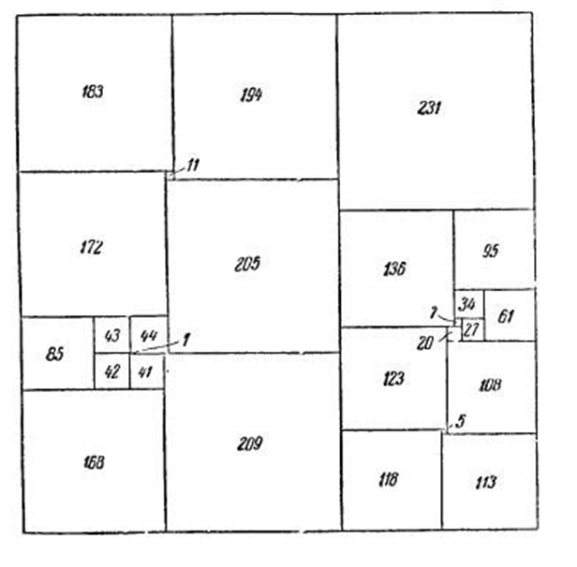Рис. 3.2.

Эта любопытная задача долгое время не была решена, и многие думали, что её решить невозможно.

По содержанию это задача о составлении квадрата из нескольких квадратов, но на этот раз без разрезания их на части и усложнённая ещё требованием, чтобы стороны квадратов выражались неповторяющимися целыми числами. Число данных квадратов безразлично.

Деление квадрата на конечное число не налегающих друг на друга квадратов, никакие два из которых не равны, называется совершенное квадрирование квадрата, а квадрат, составленный из неповторяющихся квадратов, - совершенным квадратом

Некоторые математики высказывали предположение, что совершенное квадрирование квадрата невозможно. Одним из таких математиков был Г. Штейнгауз, который утверждал в своей книге «Математический калейдоскоп», что «неизвестно, можно ли разбить квадрат на неповторяющиеся квадраты».

Так как это только допускалось математиками, но не было доказано, то поиски решения продолжались, и немногим более десяти лет тому назад в зарубежных математических журналах появились, наконец, квадраты, составленные из неповторяющихся квадратов. В своей книге «Удивительный квадрат» Кордемский Б.А. и Русалев Н.В. представили квадрат, состоящий из 26 неодинаковых квадратов. (Цифры, проставленные на рисунке, означают длины сторон соответствующих квадратов). Кордемский и Русалев пишут, что можно составить квадрат также и из 28 неповторяющихся квадратов и т. д.

Не вполне выясненным остаётся пока ещё вопрос о том, является ли 26 - наименьшим возможным числом квадратов для составления совершенного квадрата [http://www.liveinternet.ru/users/2851019/post164759261].

1. Латинские квадраты

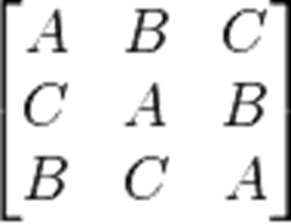
Рис. 4.2.

Латинский квадрат n-го порядка — таблица L=(lij) размеров n × n, заполненная n элементами множества M таким образом, что в каждой строке и в каждом столбце таблицы каждый элемент из M встречается в точности один раз. Пример латинского квадрата 3-го порядка:

В настоящее время в качестве множества M обычно берётся множество натуральных чисел {1,2,…,n} или множество {0,1,…,n-1}, однако Леонард Эйлер использовал буквы латинского алфавита, откуда латинские квадраты и получили своё название. Латинские квадраты существуют для любого n. История исследований латинских квадратов. Впервые латинские квадраты (4-го порядка) были опубликованы в книге «Шамс аль Маариф» («Книга о Солнце Гнозиса»), написанной Ахмадом аль-Буни в Египте приблизительно в 1200 году. Важной вехой в истории исследований латинских квадратов стала работа Эйлера. Он занимался в ней методами построения магических квадратов и предложил метод, основанный на паре ортогональных латинских квадратов. Исследуя такие пары, Эйлер выяснил, что проблема их построения подразделяется на три случая в зависимости от остатка от деления числа n на 4. Он предложил способы построения пар ортогональных квадратов для n, делящихся на 4 и для нечётных n. Очевидно, что при n = 2 таких пар не существует. Ему не удалось построить пары ортогональных латинских квадратов для n = 6, 10 и он высказал гипотезу о том, что не существует пар ортогональных квадратов для n = 4t+2. Для n = 6 он сформулировал «задачу о 36 офицерах»:

Необходимо разместить 36 офицеров шести различных полков и шести различных воинских званий в каре так, чтобы в каждой колонне и в каждом ряду был ровно один офицер каждого полка и каждого воинского звания.

В 1890 году Кэли вывел формулу для числа латинских прямоугольников из двух строк.

В 1900 году гипотеза Эйлера для n = 6 была подтверждена G. Tarry. Он построил все 9408 нормализованных латинских квадратов, разбил их на 17 типов и показал, что при любом их сочетании невозможно построить пару ортогональных квадратов. Таким образом, он отрицательно решил «задачу о 36 офицерах». В 1922 году MacNeish впервые применил теоретико-групповой подход к решению задач относительно латинских квадратов. В частности, он предложил метод конструирования латинских квадратов порядка n1•n2 из латинских квадратов порядков n1 и n2, при этом свойство ортогональности сохраняется. В 1925 году Fisher предложил использовать ортогональные латинские квадраты для планирования сельскохозяйственных экспериментов. В 1920—1930 годы стали интенсивно изучаться неассоциативные алгебраические структуры, что привело, в частности, к созданию теории квазигрупп, тесно связанной с изучением латинских квадратов, так как между латинскими квадратами и таблицами Кэликвазигрупп существует взаимно-однозначное соответствие. В 1959 году Bose и Shrikhande построили 2 ортогональных латинских квадрата для n = 22, а в1960 году они же и Parker построили с использованием ЭВМ минимальный контр пример для n = 10. Таким образом, спустя 177 лет гипотеза Эйлера была опровергнута [https://goo.gl/PwYeks].

1. Квадрат Малевича

Квадрат Малевича. Одна из самых известных картин, которая «прославляет» квадрат. Казалось бы, что может быть проще: на белом фоне черный квадрат. Любой человек, наверное, может нарисовать такое. Но вот загадка: черный квадрат на белом фоне - картина русского художника Казимира Малевича, созданная еще в начале века, до сих пор притягивает к себе и исследователей, и любителей живописи.

Углубимся в историю картины. Рассказывают, что Малевич, написав "Черный квадрат", долгое время говорил всем, что не может ни есть, ни спать. И сам не понимает, что такое сделал. И действительно, эта картина - результат, видимо, какой-то сложной работы. Когда мы смотрим на черный квадрат, то под трещинами видим нижние красочные слои - розовый, зеленый, по-видимому, была некая цветовая композиция, признанная в какой-то момент несостоявшейся и записанная черным квадратом. Художник впоследствии много думал о черном квадрате, писал теоретические работы, связывал его с космическим сознанием. Малевич считал, что "Черный Квадрат" - это вершина всего. Если ты предпочитаешь квадрат всем остальным геометрическим фигурам, то твои отличительные качества - трудолюбие, усердие, потребность доводить начатое дело до конца, упорство в достижении цели. Выносливость, терпение и методичность, как правило, делают тебя высококлассным специалистом в своей области. Ты предпочитаешь раз и навсегда заведенный порядок: всё должно находиться на своём месте и приходить в своё время. Для тебя идеал – жизнь, распланированная и предсказуемая, «сюрпризы» и изменения привычного хода событий тебе не по душе [http://mobile.studbooks.net/1132401/kulturologiya/chyornyy_kvadrat_malevicha].

РАЗДЕЛ 3. ГОЛОВОЛОМКИ

3.1. Задачи со спичками

1.Подобрать ключ Задание. В этой задаче из 10 спичек сложена форма ключа. Передвиньте 4 спички так, чтобы получилось три квадрата.

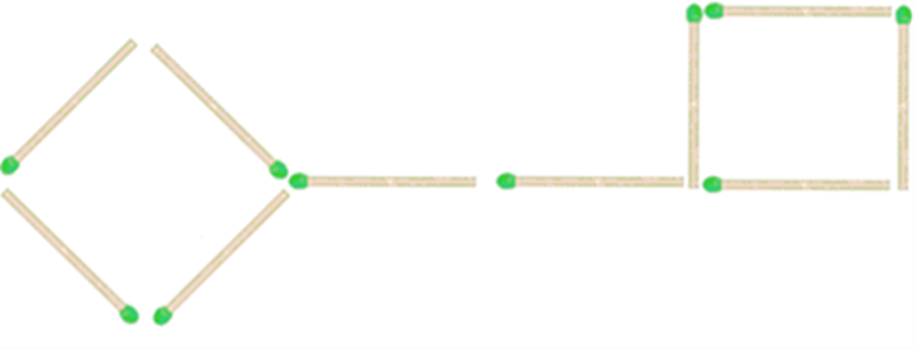
Рис. 5.3.

Ответ. Задача решается достаточно просто. Четыре спички, образующие ту часть ручку ключа, нужно переместить на стержень ключа, так чтобы 3 квадрата были выложены в ряд.

Рис. 6.3.

2. Поле для крестиков-ноликов. Условие. Необходимо переложить 3 спички так, чтобы получить ровно 3 квадрата.

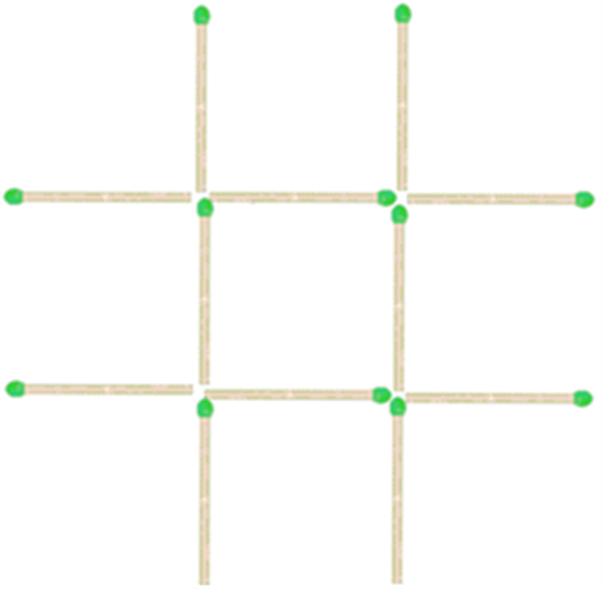
Рис. 7.3.

Ответ. Чтобы получить ровно три квадрата в этой задаче необходимо переместить 2 нижних вертикальных спички вправо и влево соответственно, чтобы они замыкали боковые квадраты. А нижней центральной горизонтальной спичкой нужно замкнуть верхний квадрат.

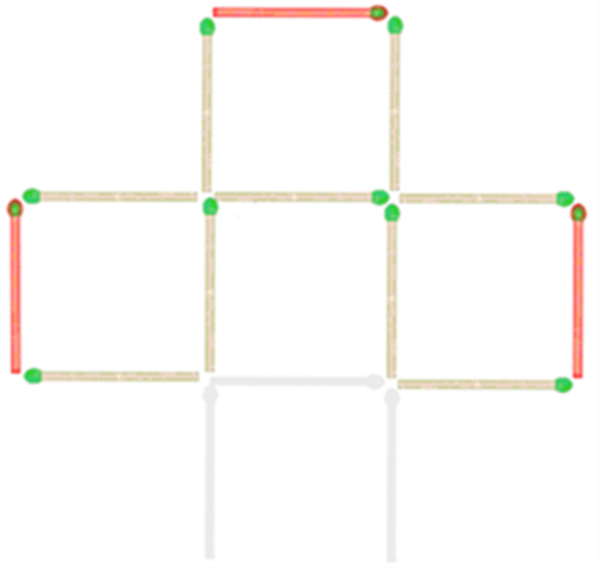
Рис. 8.3.

3.Пять из девяти Условие. Перед Вами девять маленьких квадратов, образованных двадцатью четырьмя спичками. Уберите 8 спичек, не трогая остальных, чтобы осталось всего лишь 2 квадрата.

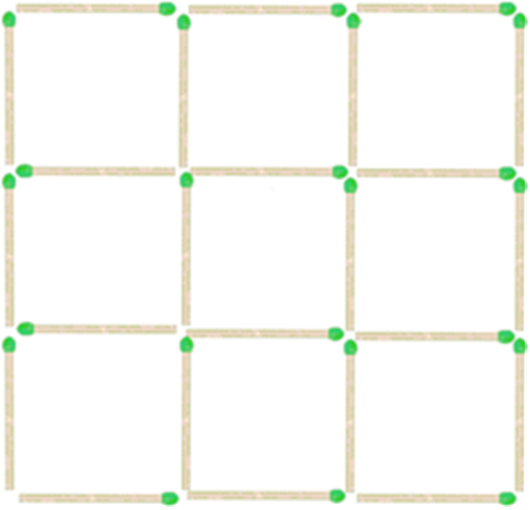
Рис. 9.3.

Ответ. Для этой задачи я нашел 2 способа решения.

Первый способ. Убрать спички так, чтобы остался только самый большой квадрат, образованный крайними спичками и самый маленький квадрат в центре, состоящий из 4 спичек.

Рис. 10.3.

Второй способ. Также оставить самый большой квадрат из 12 спичек, а также квадрат 2 на 2 спички. У последнего квадрата 2 стороны должны образовываться спичками большой квадрата, а 2 другие стороны должны быть в центре.

Рис. 11.3

[https://goo.gl/5meGq9].

1. Оригами

Оригами «Квадрат»

1.Базовая форма "дверь". Разверните.

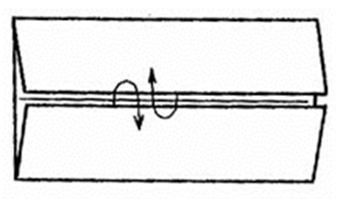
Рис. 12.3.

2.Сложите верхний правый и нижний левый уголки "долиной".

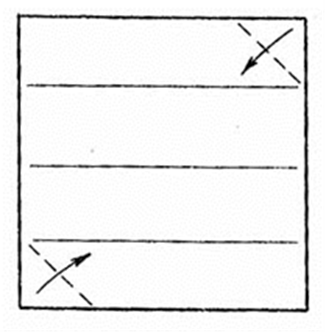
Рис. 13.3.

3.Сложите боковые стороны к центральной линии.

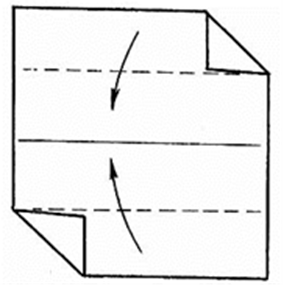
Рис. 14.3.

4.Перегните заготовку по указанным линиям, а потом разверните.

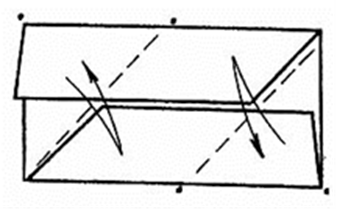
Рис. 15.3.

5. Заправьте нижний правый угол в карман.

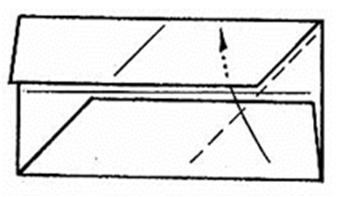
Рис. 16.3.

6.Заправьте верхний левый угол в карман.

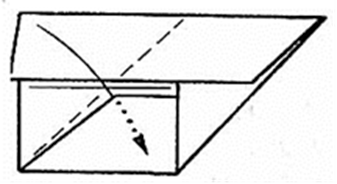
Рис. 17.3.

7.Вот что получилось. Переверните.

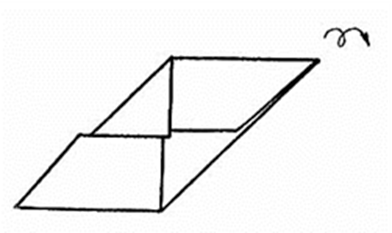
Рис. 18.3.

8.Соедините нижний и верхний правые углы и верхний и нижний левые углы. Переверните.

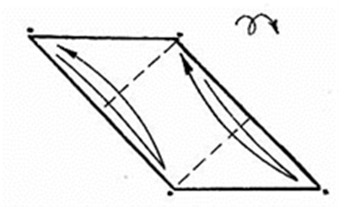
Рис. 19.3.

9. На получившейся заготовке есть два кармана и две вставки. Чтобы собрать кубик, нужно сделать еще 5 таких заготовок, а потом их собрать.

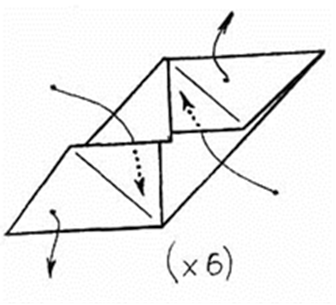
Рис. 20.3.

10. Так соединяются две заготовки.

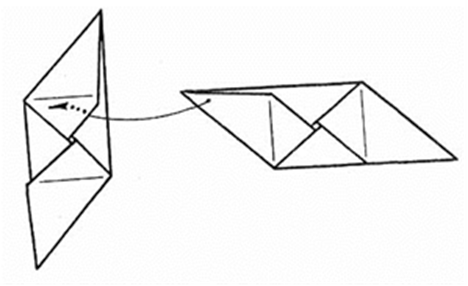
Рис. 21.3.

11.Вот что получилось. Третий модуль нужно вставить в указанный на рисунке карман.

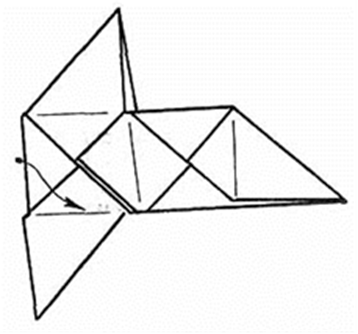
Рис. 22.3.

12.Вот что получилось. Теперь необходимо соединить еще 3 заготовки.

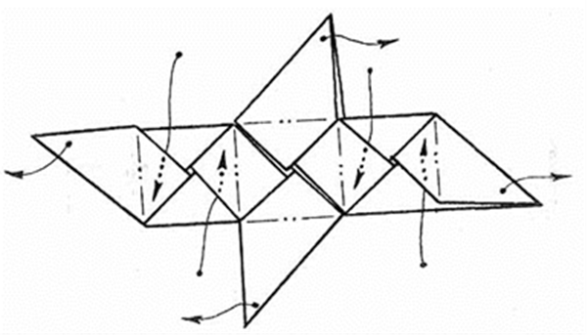
Рис. 23.3.

13.Кубик готов. Раскрасьте его грани яркими красками.

Рис. 24.3.

[http://www.zonar.info/node/72].

ВЫВОДЫ

В своей работе мы показали многие удивительные свойства квадрата, описали востребованность и применение данной фигуры в разных аспектах, а также показали на практике такие интересные задания, как оригами и задачи со спичками. Во время работы над данным рефератом мы изучили полезную литературу и узнали много чего интересного об этой замечательной фигуре. Мы считаем, что поставленные нами цели были достигнуты.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

ИНТЕРНЕТ-РЕСУРСЫ

1. https://uchiuroki.ru/teenager/interestingfact/kvadrat/

2. http://festival.1september.ru/articles/565187/

3. http://interesko.info/kvadrat-pifagora/

4. http://www.new-numerology.ru/lab-kv_p.htm

5. http://www.zonar.info/node/72

6. https://goo.gl/5meGq9

7. http://www.liveinternet.ru/users/2851019/post164759261

8. https://goo.gl/PwYeks

9. http://mobile.studbooks.net/1132401/kulturologiya/chyornyy_kvadrat_malevicha