От абака до компьютера
Оглавление
ВВЕДЕНИЕ 2
ГЛАВА 1. ВРЕМЯ ВЫКЛАДЫВАТЬ КАМУШКИ: АБАК И СЧЕТЫ 3
Абак 4
Счеты 6
ГЛАВА 2. ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА 7
ГЛАВА 3. МЕХАНИЧЕСКИЕ СЧЕТНЫЕ ПРИБОРЫ 8
ГЛАВА 4. ВЫЧИСЛИТЕЛЬНАЯ МАШИНА БЭББИДЖА 11
ГЛАВА 5. ТЕРНИСТЫЙ ПУТЬ К ЭВМ…………………….……………………12
ГЛАВА 6. ПЕРВЫЕ ЭВМ…………………………………………………..………14
ЗАКЛЮЧЕНИЕ……………………………………………………………………...16
СПИСОК ЛИТЕРАТУРЫ………………………………………………………..…17
ВВЕДЕНИЕ
В наше время учиться считать и делать первые вычисления дети начинают очень рано. Пожалуй, едва научившись ходить, ребенок уже различает количество предметов в пределах пяти. А к возрасту 5-6 лет многие дети владеют арифметическими действиями и уж точно знают, для чего нужен калькулятор или компьютер.
Этому способствует информационная среда, окружающая ребенка: общение в семье, развивающие занятия в детском саду и специальные программы быстрого счета для малышей.
Но к такому удивительному результату человечество шло тысячи лет.
Считать, или шире– вычислять люди научились устно, письменно и с помощью специальных инструментов. В разные времена и инструменты использовались разные: счетные доски, абаки, приспособления, приборы, машины и, с середины прошлого столетия – компьютеры.
В моей проектной работе я постаралась проследить развитие счетных устройств от древности до современности.
Цель данной работы: обозначить основные этапы развития вычислительной техники.
Основные задачи проекта:
Рассмотреть историю развития вычислительной техники и выявить моменты времени, в которые были созданы новые вычислительные устройства.
Привести изобретателя и место изобретения устройства.
Обозначить принцип работы рассматриваемого устройства.
Проектный продукт: электронная презентация
План работы:
Выбор наиболее интересной темы
Сбор и анализ информации по теме: работа с литературой и Интернет-ресурсами
Определение основных этапов развития счетных устройств и распределение их в хронологическом порядке
Работа над пояснительным текстом проекта и создание презентации
ГЛАВА 1. ВРЕМЯ ВЫКЛАДЫВАТЬ КАМУШКИ: АБАК И СЧЕТЫ
Самым древним счетным инструментом, который природа предоставила в распоряжение человека – были его собственные руки.
По мнению многих специалистов, изучавших историю развития счета, числа 5 и 10, как основа счета связаны с «пальцевым» счетом. Кисть руки - пясть - синоним и основа числительного «пять» в разных языках мира. А число 10 (количество пальцев на двух руках) – основание десятичной системы счисления.
В этой связи приведу высказывание математика Николая Николаевича Лузина (1883-1950), создателя Московской математической школы. «Преимущества десятичной системы счисления не математические, а зоологические. Если бы у нас на руках было не 10, а 8 пальцев, то человечество бы пользовалось восьмеричной системой счисления»
Как известно, в десятеричной системе счисления значение цифры зависит от позиции и при перемещении на одно место изменяет свое значение в 10 раз. Например, число 135. В нем 1(единица) соответствует одной сотне, 3- трем десяткам, а 5-пяти единицам. Если бы 1(единица) была на втором месте, то соответствовала бы одному десятку (значение цифры уменьшилось в 10 раз).
Еще один вид инструментального счета – это деревянные палочки с зарубками, их еще называли бирками. Еще в древнем Египте на барельефах изобразили бога Тота, который отмечает на пальмовой ветви зарубками время правления фараона. Позже бирки стали использовать для учета и сбора налога. Бирку разрезали на две части так, чтобы зарубки остались на обеих частях сразу. Одна – для сборщика налога, другая – для крестьянина.
В Конго найдена кость с зарубками, которые сделаны около 20 тысяч лет до нашей эры.

Китайцы, жители Индии и американские индейцы пользовались для счета веревками и ремнями с узелками.
В наше время сохранились отголоски тех времен в виде поговорок «Заруби себе на носу» и «Узелок на память»
Абак
Первым счетным устройством (VI—V вв. до н.э.), позволившим сделать счет более удобным и быстрым, можно считать специальную доску для позиционного (поразрядного) счета, названную «абак». От латинского Abacus — доска, покрытая пылью. Примитивный абак, вероятно, таковым и был.
Впервые абак изобрели, возможно, древние вавилоняне. Это была просто деревянная дощечка, посыпанная песком.
На доске острой палочкой проводили линии и в получившихся колонках размещали какие-либо предметы (например, камушки) по позиционному принципу. На рисунке показано как складывались числа 258 и 54 на абаке. Вычитание выполнялось изъятием камушков, умножение и деление – как повторение сложения и вычитания.
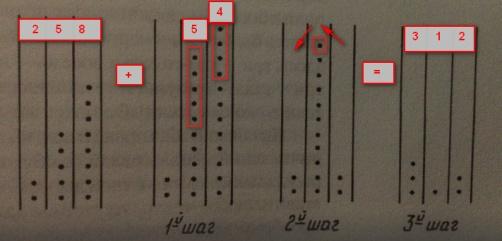
В пятом веке, как свидетельствуют историки, счётная доска благодаря финикийским купцам стала активно использоваться в Египте, Древней Греции и затем в Риме.
«Саламинская плита» - древнегреческий абак на мраморной доске размером 150 X 75 см, найденный на острове Саламин в 1948 году. Ее использовали для подсчета денег. Левые колонки служили для отсчета драхм и талантов; правые - для долей драхмы: оболов и халков. На абаке отложено: 4873 драхмы 2 обола 5 халков.
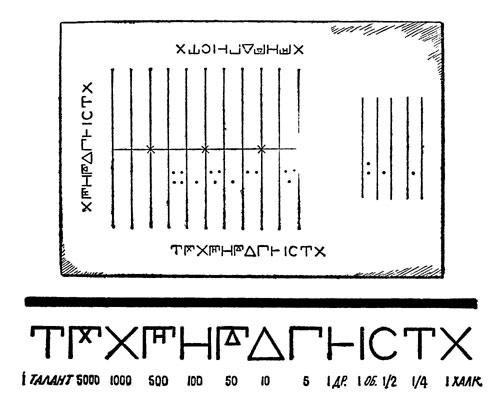
В разных странах существовало несколько видов абака: древнеегипетский (заимствован греками), римский, китайский (суаньпань), японский (соробан).
Египетский абак – это разлинованная дощечка. В ее столбцах размещали камешки. Столбцы пересекала черта, над ней размещали камешек, заменявший пять камешков, расположенных под чертой. Египтяне, в отличие от греков передвигали камешки справа налево, греки же – наоборот.
В древнем Риме абак назывался calculi и изготавливался из бронзы, слоновой кости и цветного стекла. Слово calculus означало «галька», от него позднее произошло слово calculatore (вычислять) и известное нам слово «калькуляция».
Сохранился бронзовый римский абак, на котором галька передвигалась в прорезанных желобках.

Этот инструмент позволял выполнять все 4 действия арифметики и работать с дробями.
В Китае для вычислений использовали бамбуковые палочки, которые в определенном порядке раскладывались на счетной доске.
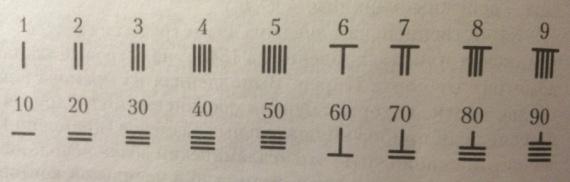

Суаньпань (Китай)
Постепенно абак эволюционировал. В 10-м веке линии счета на абаке были заменены натянутыми веревками с нанизанными на них косточками (или бусинками). Так появился «дощаный счет».
Японский соробан вероятно происходил от китайского суаньпаня, который был завезен в Японию в 15-16 веках. Соробан проще: у него на «небе» и на «земле» на одну косточку меньше. Костяшки сделали заостренными и расстояние между ними и перегородкой уменьшили, что позволило ускорить процесс счета.

Счеты
В конце 16 начале 17 веков появился русский абак – счеты. Долгое время считалось, что счеты, как и японский соробан, ведут свое происхождение от китайского суаньпаня. Но русский ученый И.Г. Спасский в 60-х годах 20 в. доказал русское происхождение этого прибора.
Особенность русских счет – горизонтальное расположение спиц с косточками и использована десятичная, а не пятеричная система счисления. Десятичный принцип счисления был впервые в мире был применен именно в денежном деле России. Елена Глинская, мать Ивана Грозного, провела денежную реформу. С тех пор рубль стал делиться на 100 основных единиц (копеек).


Проще всего на счётах выполнять операции сложения и вычитания. В 19-20 в.в. счеты стали использовать в школах, в качестве учебного пособия при начальном обучении.
ГЛАВА 2. ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
Следующий прорыв в технике вычислений был связан с появлением такого счетного устройства, как логарифмическая линейка.
Развитие экономики стран требовало более сложных вычислений. Умножение, деление, возведение в степень, вычисление квадратных и кубических корней из больших чисел требовало огромного количества времени. Шотландский изобретатель, владелец обширных сельскохозяйственных угодий, Джон Непер, занимался наукой ради удовлетворения жажды знаний, проявил себя как гений математики. Он создал правила, которые каждое умножение и деление превращали в чистое сложение и вычитание. Его идеи признали европейские математики и слово «Логарифм» вошло в словарь математиков. Непер создал первые логарифмические таблицы. Его последователь профессор математики Генри Бригс продолжил работу по созданию логарифмических таблиц. Его называли английским Архимедом.
Ученик Бригса Эдмунд Гюнтер в 1620 году придумал, как механизировать вычисления и создал прибор на основе логарифмических таблиц Бригса: он взял медную пластинку и отметил на ней отрезки, которые соответствуют различным числам из таблицы, с помощью двух циркулей-измерителей и этой шкалы выполнялись сложные вычисления.
Но Гюнтер использовал свое изобретение только в педагогических целях и мало кто знал о нем. Лондонский юрист Эдмунд Уингейт был впечатлен этим изобретением, сделал его всеобщим достоянием, кроме того, усовершенствовал его.
Прибор становился все сложнее. В 1622г. Британский математик Уильям Оутред использовал устройство Гюнтера как прототип и создал счетный прибор, который мы сейчас называем логарифмической линейкой. С тех пор ее продолжали усовершенствовать. В широкую инженерную практику ее ввел изобретатель паровой машины Джеймс Уатт на своем машиностроительном заводе. К концу 20 века (совсем недавно!) она стала выглядеть так.

Этот прибор около четырех столетий был главным инструментом для научных и инженерных расчетов. Пока только в 1970 г ее не заменили электронные микрокалькуляторы.
ГЛАВА 3. МЕХАНИЧЕСКИЕ СЧЕТНЫЕ ПРИБОРЫ
Одним из этапов развития счётных приборов стало изобретение в 17-м веке суммирующих машин.
«Паскалина» - суммирующая машина Блеза Паскаля
Блез Паскаль начал создавать суммирующую машину «Паскалину» в 1642-м году в возрасте 19-ти лет, наблюдая за работой своего отца, который был интендантом (сборщиком налогов) в Руане и часто выполнял долгие и утомительные расчёты.
Машина Паскаля представляла собой механическое устройство в виде ящичка с многочисленными связанными одна с другой шестерёнками (зубчатыми колёсами). Складываемые числа вводились в машину при помощи соответствующего поворота наборных колёсиков. На каждое из этих колёсиков, соответствовавших одному десятичному разряду числа, были нанесены деления от 0 до 9.

Паскаль трудился над ней 5 лет, изготовил около пятидесяти экземпляров в разных вариациях, добился, как сейчас говорят, патента на изобретение и наладил серийное производство. До наших дней дошли 8 экземпляров этого устройства.
Позже, усовершенствовав механизмы, Готфрид Лейбниц и Шарль де Кольмар создали другие механические машины. С тех пор механические счетные машины, которые могли выполнять 4 действия арифметики, стали называть арифмометрами.
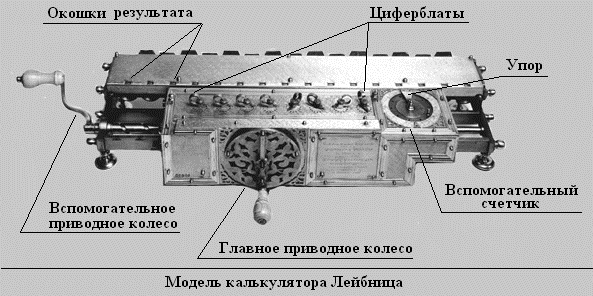
Арифмометр Однера – это успешная разновидность арифмометров, разработанная русским ученым шведского происхождения Вильгодтом Теофилом Однером. В Санкт-Петербурге в 1890 году было налажено их промышленное производство. В 1890 г было продано 500 арифмометров. В течение последующих пяти лет в России было продано 4000 арифмометров и 1000 штук за границу.
В 1891 году Однер получил патент на свой улучшенный арифмометр в Германии и на его основании открыл филиал своего завода в Берлине.
Преимущества:
Малые размеры
Простое и прочное устройство
Абсолютно верное и быстрое действие (4 арифметические действия и возможность извлекать корни)
Просто изучить, как обращаться
Недостатки:
Большое количество спиральных пружин в подвижной части (каретке). Из-за этого возникали ошибки при переноске десятков. Устранен в более поздних конструкциях.
Высокий уровень шума при работе
Вращение рукоятки в различные стороны в зависимости от выполняемого арифметического действия
В 1913 году в России работало 22 тысячи арифмометров.
В советские времена, после революции 1917 года, выпуск арифмометров был возобновлен на механическом заводе в Москве им. Феликса Дзержинского и выпускались под маркой «Оригинал-Однер». С 1931 года они стали известны как «Феликс» (В народе их называли «Железный Феликс»). Этот арифмометр служил долгие годы, был самым надежным и популярным. В обслуживании был прост и требовал только смазки.


Механические счетные устройства использовали почти до конца 20 века. На их принципе действия были основаны первые кассовые аппараты.

ГЛАВА 4. ВЫЧИСЛИТЕЛЬНАЯ МАШИНА БЭББИДЖА
Британский изобретатель Бэббидж был очарован механикой и математикой. Его увлекала идея Лейбница о системе символов. Его машина не просто рассчитывала, она была способна провести анализ операции и выполняла вычисления с помощью набора правил, последовательности операций (сейчас называемых алгоритмами) и выдавала результат с помощью символов.

Описание принципа работы машины и первую в мире программу для этой машины составила Ада Лавлейс, дочь английского поэта Байрона.
Ее считают первым программистом, а машину Бэббиджа – прототипом компьютера.
В 1823 году эту машину начали создавать на деньги казначейства Англии, но в 1842 году Министерство финансов посчитало нецелесообразным финансирование этого проекта и прекратило его.
Тем не менее, создание этой машины стало первым шагом на пути появления компьютеров в будущем.
ГЛАВА 5. ТЕРНИСТЫЙ ПУТЬ К ЭВМ
В 1847 году еще один английский ученый, Джордж Буль, способствовал развитию математических наук: кибернетики и информатики.
Начало было положено после выхода его статьи « Математический анализ логики» в 1847 году, а позже, в 1854 году вышел его капитальный труд «Исследование законов мышления, на которых основываются математические теории логики и вероятностей». Суть его работ была в применении алгебраической символики к обработке логических высказываний. Была предложена система правил для формализации логических задач.
Например: простая логика содержит два элемента 0 (ложь, «нет») и 1 (истина, «да») и две операции «/» («и») и «.» («или»)
Таким образом, созданный Булем логический аппарат, который называли булевой алгеброй, через 100 лет объединили с двоичной системой счисления, и это стало основой для разработки электронного компьютера.
Например: при оценке высказывания, учитывались только два возможных значения: оно ложно или истинно - «нет / да», что в двоичном коде выглядело как 0 или 1 - «0/1». Это можно применить к простейшему переключателю в электронных системах. Он может находиться только в двух положениях: выключен/включен (ток не пропускает/ток пропускает)
Для логических действий можно ввести операции, подобные арифметическим действиям.
Назову три наиболее важные операции:
«И» - соединение (конъюнкция), обозначается (Λ)
«ИЛИ» - разъединение (дизъюнкция), обозначается ( V )
«НЕ» - отрицание, обозначается ( ¬ )
Действия булевой алгебры в двоичном коде определяются следующим образом:
| 0 и 0= 0 | 0 или 0= 0 | НЕ 0 =1 |
| 0 и 1= 0 | 0 или 1= 1 | НЕ1 =0 |
| 1 и 0= 0 | 1 или 0= 1 |
|
| 1 и 1= 1 | 1 или 1= 1 |
|
Комбинируя эти три основных действия, можно осуществить и более сложные операции: например логическое сложение кодов. В любых машинах эта операция была необходима.
Работам Буля при жизни уделялось недостаточно внимания, но после его смерти нашлись сторонники его теории. Первым из их стал логик Чарлз Пирс, который познакомил американцев в 1867г. с булевой алгеброй.
Через несколько десятилетий в докторской диссертации Клода Шеннона, положившей начало теории информации, были связаны воедино численная двоичная система, булева алгебра и реализация вычислительных процессов в виде электрических схем. Одновременно с ним в Московском университете русский ученый Виктор Шестаков предложил использовать булеву алгебру как логическую основу для создания электронно-вычислительных машин.
Логических символов (кванторов) со временем стало больше. Многие из них мы используем на уроках математики для записи формул и доказательств.
Например: ॥ - параллельно, = - следует, ∩ - пересечение и др.
ГЛАВА 6. ПЕРВЫЕ ЭВМ
С начала 30-х годов 20 века начали создаваться и к 1940 году появились первые счетные электронные машины на основе цифровых переключателей – электронных ламп и цифровых реле.
Математик фон Нейман описал основные компоненты вычислительной машины: процессор, память, блоки ввода/вывода. Отмечал, что такое устройство должно работать в двоичной системе, быть электронным, а не механическим и что команды должны выполняться последовательно (исполнение программы)
Что касается программ, то работу первой программистки Ады Лавлейс целых сто лет спустя продолжил Алан Тьюринг. В 1950 году в печать вышла его статья «Может ли машина мыслить?» В ней он подробно разобрал научные выводы леди Лавлейс. Некоторыми терминами, которые она использовала в своих трудах, до сих пор пользуются программисты. Например, «рабочие ячейки», «цикл».
Алан Тьюринг стал отцом современного компьютера. Его идея компьютера состояла из ленты, символов и конфигураций. Лента выполняет ту же роль, что и бумага в пишущей машинке, но двигается только в одном направлении. Лента разбита на квадраты (ячейки). В каждый момент времени в компьютере находится лишь один квадрат ленты.
Символы записываются на ленте по одному в каждой ячейке. Тьюринг предложил минимальное количество символов – два: ноль и единица. В каждый момент времени машина «знает» только об одном символе, о том, который находится в единственной ячейке внутри.
Кофигурации – это инструкции для машины, что делать, это как «состояние ума». Например, в конфигурации А – лента может продвинуться вправо, если текущий символ «1», в конфигурации В может стереть текущий символ.
Тьюринг заключил: «Все, что можно вычислить, может вычислить эта машина»
Первую простую счетную электронную машину создал немецкий инженер Конрад Цузе. Она была единственной в Европе работающей моделью.
Конрад Цузе родился в Берлине в 1910 году, начал работу над машиной в 1934 году , когда был еще студентом. Друзья помогли ему финансово, и он начал работу над изобретением в скромных условиях дома своих родителей, на маленьком столе. Постепенно его машина стала занимать около 4 м2 и располагалась в центре комнаты. Его третья модель вычислительной машины «Зет-3» хранится в Немецком техническом музее в Берлине.
Цузе создал первый в мире алгоритмический язык и продолжил работу на новом месте жительства в Швейцарии, где он основал компанию по производству вычислительной техники. В 1950 году доработанная модель «Зет-4» была единственным компьютером в Европе, опередившей американские разработки. И к 1967 году его компания выпустила более 250 компьютеров.
Параллельно с Цузе, вычислительные машины создавались и в США.
В 40-е годы 20 века ЭВМ (электронно-вычислительные машины) обеспечивали огромную по тем временам скорость вычислений - несколько тысяч операций в секунду.
Над созданием прототипами будущих компьютеров трудилась группа ученых около 50 человек. Первые модели имели названия ЭНИАК, ЭДВАК, УНИВАК – это аббревиатуры их сложных названий. Например, УНИВАК – это универсальный автоматический компьютер.
ЭНИАК, ЭДВАК, УНИВАК разработаны в США командой инженеров и учёных во главе с Джоном Преспером Экертом и Джоном Уильямом Мокли при активной помощи математиков фон Неймана, Германа Голдстайна и Гарри Хаски.
ЭНИАК был введен в эксплуатацию в 1945 году, после войны. Машина состояла из 17 тысяч электронных ламп и полутора тысяч реле. Он был огромен: весил 30 тонн, 26 метров в длину, 3 метра в высоту. Он делал 5000 сложений и 300 умножений в секунду.
Но, когда он работал, температура в помещении поднималась до 50 градусов по Цельсию. Он потреблял огромное количество электричества. Ходили слухи, что когда его включали, вся Филадельфия оставалась без света.
В России свой вклад в развитие ЭВМ внес академик Лебедев Сергей Алексеевич. Он был современником Конрада Цузе, Алана Тьюринга. Под его руководством вышли полтора десятка моделей отечественных компьютеров: первые из них МЭСМ (малая электронно-счетная машина) и БЭСМ (большая счетно-вычислительная машина).
В 1960 годах электронные лампы заменили транзисторами, переключателями, которые состояли из полупроводников электрического тока (вещества, которые проводят ток только в одном направлении). Эти новшества позволили уменьшить размеры компьютеров и повысить их надежность. Компьютеры уменьшались в размерах примерно вдвое каждые 18 месяцев (1,5 года)
ЗАКЛЮЧЕНИЕ
Современные компьютеры позволяют выполнять фантастически сложные расчеты в невероятно короткий срок. Они посчитают за несколько минут то, что несколько вычислителей делали бы годы.
Работая над проектом, я сделала следующий вывод:
В развитии счетных устройств, пройдена дорога длиною в тысячелетия. Но быстрее всего они развивались в 20 веке, а последние 30 лет настолько стремительно, что мы не успеваем следить за их новыми моделями и уже не знаем имена разработчиков, поскольку работают команды ученых из десятков человек.
Электронные устройства и компьютеры стали общедоступны, количество единиц вычислительной техники на нашей планете исчисляется миллиардами.
Таким образом, современный мир переживает информационную революцию и человечество ждут перемены настолько радикальные, что к ним заранее очень сложно подготовить свое сознание.
СПИСОК ЛИТЕРАТУРЫ:
Альбов А.С. От абака до кубита/ Александр Альбов.- 2-е изд.-СПб.: Страта,2016.-178с., ил.
Полунов Ю.Л. От абака до компьютера: судьбы людей и машин. Книга для чтения по истории вычислительной техники в двух томах. Том I.- М.: Издательско-торговый дом «Русская Редакция», 2004. – 480с.:ил
http://mathemlib.ru Библиотека по математике.
http://megabook.ru Универсальная энциклопедия Кирилла и Мефодия
https://yandex.ru/images Изображения.

































