"Решение двойных неравенств"

А. Нивен

Запомним

Решить систему неравенств – это значит найти значение переменной , при котором верно каждое из неравенств системы.

Запомним

Если надо решить систему неравенств, то :

• решаем каждое неравенство системы отдельно

• изображаем полученные решения на числовой прямой и смотрим пересечения этих решений.

Эта общая часть и является решением данной системы неравенств.

2 и y 14, то х + y 16? 2. Верно ли утверждение: если х 2 и y 14, то х . y 3. Является ли число 0 решением неравенства 3х – 1 4. Является ли неравенство 3 х + 12 2 х – 2 строгим? 5. Существует ли целое число, принадлежащее промежутку [– 2,5; – 2,3]? 6. Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число, знак неравенства не меняется? " width="640"

ТЕСТ

1. Верно ли утверждение: если х 2 и y 14, то х + y 16?

2. Верно ли утверждение: если х 2 и y 14, то х . y

3. Является ли число 0 решением неравенства 3х – 1

4. Является ли неравенство 3 х + 12 2 х – 2 строгим?

5. Существует ли целое число, принадлежащее промежутку [– 2,5; – 2,3]?

6. Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число, знак неравенства не меняется?

6 2х – 4 3 Решение: решим каждое неравенство отдельно 5х + 1 6 2х – 4 3 5х 6 -1 2х 5х 5 2х х 1 х 3,5 1 3,5 х Ответ: (1; 3,5) " width="640"

Решим систему неравенств (состоящую из линейных неравенств)

5х + 1 6

2х – 4 3

Решение: решим каждое неравенство отдельно

5х + 1 6 2х – 4 3

5х 6 -1 2х

5х 5 2х

х 1 х 3,5

1 3,5 х

Ответ: (1; 3,5)

- 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4 ] " width="640"

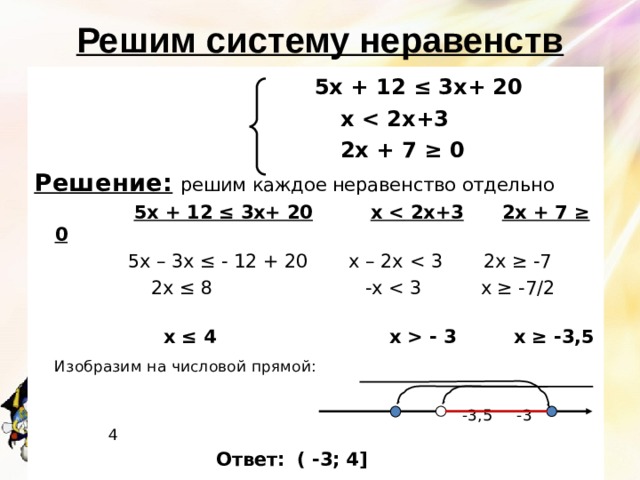
Решим систему неравенств

5х + 12 ≤ 3х+ 20

х 2х+3

2х + 7 ≥ 0

Решение: решим каждое неравенство отдельно

5х + 12 ≤ 3х+ 20 х 2х+3 2х + 7 ≥ 0

5х – 3х ≤ - 12 + 20 х – 2х

2х ≤ 8 -х

х ≤ 4 х - 3 х ≥ -3,5

Изобразим на числовой прямой:

-3,5 -3 4

Ответ: ( -3; 4 ]

12 + 11х 5х – 1 ≥ 0 Проверим ответы: 1) [ 2; +∞ ) 2) Нет решения " width="640"

Работа в парах:

Решить систему

неравенств:

1) 3х – 2 ≥ х + 1

4 – 2х ≤ х – 2

2) 3х 12 + 11х

5х – 1 ≥ 0

Проверим ответы:

1) [ 2; +∞ )

2) Нет решения

Примеры двойных неравенств

Прочитайте неравенства :

-6 х 0

-1,2 ≤ х 3,5

0 х ≤ 5,9

0 4х + 2 ≤ 6 Решим каждое неравенство системы отдельно: 1) 4х + 2 0 2) 4х + 2 ≤ 6 х - 0,5 х ≤ 1 Полученные результаты изобразим на числовой прямой: -0,5 1 х Ответ: -0,5 х ≤ 1 или (-0,5; 1 ] " width="640"

Решение двойных неравенств

Решить неравенство: 0 4х +2 ≤ 6

Решение: составим систему: 4х + 2 0

4х + 2 ≤ 6

Решим каждое неравенство системы отдельно:

1) 4х + 2 0 2) 4х + 2 ≤ 6

х - 0,5 х ≤ 1

Полученные результаты изобразим на числовой прямой:

-0,5 1 х

Ответ: -0,5 х ≤ 1 или (-0,5; 1 ]

Решите неравенства, работая в парах

Решить неравенства:

Проверим

ответы:

1) [ -1; 2 ]

2) (2,5; 7 ]

3) [ - 1,5; - 1)

4) (-2; 1)

5) (-4; 0)

• -6 ≤ - 3х ≤ 3
• 4 2х – 1 ≤ 13
• -2 ≤ 6х + 7 1
• 0,3 0,5 + 0,1х 0,6

• 0 - 2х 8

9/4=2,25 Полученные результаты изобразим на числовой прямой: 1 2,25 4 х Ответ: [ 4; + ∞ ) " width="640"

Решим систему неравенств (в которую входит квадратное неравенство)

Решить систему неравенств: х ² - 5х + 4 ≤ 0

9 - 4х 0

Решение: решим каждое неравенство системы отдельно

1) х ² - 5х + 4 ≤ 0 2) 9 - 4х 0

х ² - 5х + 4 = 0 - 4х

т.к. а+в+с=0, то х 1 =1; х 2 =4 х 9/4=2,25

Полученные результаты изобразим на числовой прямой:

1 2,25 4 х

Ответ: [ 4; + ∞ )

0 Решение: решим каждое неравенство отдельно х ² - 3х + 2 0 2х ² - 3х – 5 0 Найдем корни соответствующих квадратных уравнений х ² - 3х + 2 = 0 2х ² - 3х – 5 = 0 По свойствам коэффициентов имеем: х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (- ∞; -1) υ (2,5; +∞) " width="640"

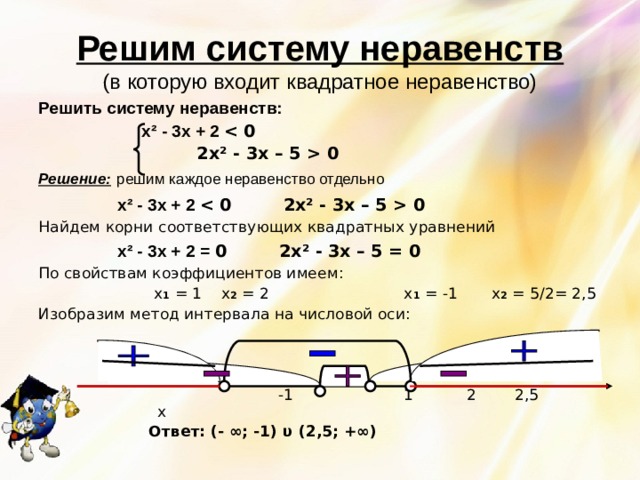
Решим систему неравенств (в которую входит квадратное неравенство)

Решить систему неравенств:

х ² - 3х + 2 0

2х ² - 3х – 5 0

Решение: решим каждое неравенство отдельно

х ² - 3х + 2 0 2х ² - 3х – 5 0

Найдем корни соответствующих квадратных уравнений

х ² - 3х + 2 = 0 2х ² - 3х – 5 = 0

По свойствам коэффициентов имеем:

х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5

Изобразим метод интервала на числовой оси:

-1 1 2 2,5 х

Ответ: (- ∞; -1) υ (2,5; +∞)

0 4х – 1 ≥ 0 2) 4х ² - 1 ≤ 0 х ² 1 3х ² - 2х – 1 0 х ² - х – 6 0 " width="640"

Решим системы неравенств, работая вместе

1) 6х ² - 5х + 1 0

4х – 1 ≥ 0

2) 4х ² - 1 ≤ 0

х ² 1

• 3х ² - 2х – 1 0

х ² - х – 6 0

0 4х – 1 ≥ 3 3) 2х ² - 7х + 5 0 2 – х ≥ 0 Проверим ответы: 1) (4; 9 ] 2) [ 1; 2) 3) (- ∞ ; 1 ) " width="640"

Решите системы неравенств, работая самостоятельно

1) х ² - 10х + 9 ≥ 0

12 – 3х 0

2) 2х ² - 5х + 2 0

4х – 1 ≥ 3

3) 2х ² - 7х + 5 0

2 – х ≥ 0

Проверим ответы:

1) (4; 9 ]

2) [ 1; 2)

3) (- ∞ ; 1 )