Решение квадратных неравенств

Решение квадратичных неравенств

(метод парабол)

Урок алгебры в 9 классе

Учитель математики

высшей квалификационной категории

МКОУ «Ванашимахинская СОШ» Расулова Р.А.

0, запиши ответ у проверка 2 х 0 X (1;5) 3 далее " width="640"

1

Найди решение f(x)0, запиши ответ

у

проверка

2

х

0

X (1;5)

3

далее

2

f(x)

у

4

проверка

х

0

X (-∞;-2)U(2;+∞)

2

далее

0 у 0 2 проверка х -2 Решений нет далее " width="640"

3

f(x)0

у

0

2

проверка

х

-2

Решений нет

далее

0 у проверка X (-∞;+∞) 1 х 1 0 далее " width="640"

4

f(x)0

у

проверка

X (-∞;+∞)

1

х

1

0

далее

5

f(x)

у

проверка

Решений нет

2

х

2

0

далее

6

f(x)

у

0

-3

х

проверка

X (-∞;-3)U(-3;+∞)

-7

проверить тест

далее

3х² " width="640"

Квадратичные неравенства

Неравенство вида

ах ²+bх+с 0, ах²+bх+с≥0), где а, b, с-любые числа, а≠0, называется квадратичным.

Например: а) 2х²≥0

б) -4х²+8

в) 2х-х²≤0

г) 14х+53х²

0). Нули функции: 5x²+9x-2=0 X 1 =-2; X 2 =0,2 X 0,2 -2 yОтвет: (-2;0,2) " width="640"

5x²+9x-2

Рассмотрим функцию y=5x²+9x-2

Графиком является парабола, ветви вверх (а=5, а 0).

Нули функции:

5x²+9x-2=0

X 1 =-2; X 2 =0,2

X

0,2

-2

y

Ответ: (-2;0,2)

Чтобы решить квадратичное неравенство методом парабол, надо:

• Рассмотреть функцию у=ах ²+bх +с, определить направление ветвей;
• Найти нули функции, решив квадратное уравнение ах²+bх+с=0;
• Схематически построить параболу, учитывая направление ветвей и точки пересечения с осью х;
• Учитывая знак неравенства, выбрать нужные промежутки и записать ответ.

0 Рассмотрим функцию y=3x²-11x-4 Графиком является парабола, ветви вверх (а=3, а 0). Нули функции: 3x²-11x-4=0 X 1 =-1 / 3; X 2 =4 X 4 -1 / 3 y0 при x (-∞; -1 / 3 )U(4; +∞) Ответ: (-∞; -1 / 3 )U(4; +∞) " width="640"

3x²-11x-4 0

Рассмотрим функцию y=3x²-11x-4

Графиком является парабола, ветви вверх (а=3, а 0).

Нули функции:

3x²-11x-4=0

X 1 =-1 / 3; X 2 =4

X

4

-1 / 3

y0 при x (-∞; -1 / 3 )U(4; +∞)

Ответ: (-∞; -1 / 3 )U(4; +∞)

-1/4x²+2x-4

Рассмотрим функцию y=-1/4x²+2x-4

Графиком является парабола, ветви вниз (а=-1/4, а

Нули функции:

-1/4x²+2x-4=0

4

X

X 1,2 =4

y

Ответ: (-∞; 4)U(4; +∞)

0 Рассмотрим функцию y=x²-3x+4 Графиком является парабола, ветви вверх (а=1, а 0). Нули функции: x²-3x+4=0 D График функции с осью ox не пересекается y0 при x (-∞; +∞) Ответ: (-∞; +∞) X 13 " width="640"

x²-3x+4 0

Рассмотрим функцию y=x²-3x+4

Графиком является парабола, ветви вверх (а=1, а 0).

Нули функции:

x²-3x+4=0

D

График функции с осью ox

не пересекается

y0 при x (-∞; +∞)

Ответ: (-∞; +∞)

X

13

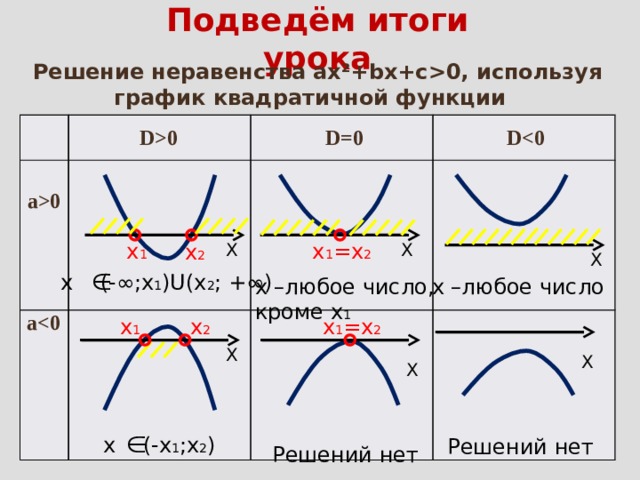0, используя график квадратичной функции D0 D=0 D a0 x 1 =x 2 x 1 X X x 2 X x (-∞;x 1 )U(x 2 ; +∞) x –любое число, кроме x 1 x –любое число a x 2 x 1 x 1 =x 2 X X X x (-x 1 ;x 2 ) Решений нет Решений нет " width="640"

Подведём итоги урока

Решение неравенства ах²+bх+с0, используя график квадратичной функции

D0

D=0

D

a0

x 1 =x 2

x 1

X

X

x 2

X

x (-∞;x 1 )U(x 2 ; +∞)

x –любое число,

кроме x 1

x –любое число

a

x 2

x 1

x 1 =x 2

X

X

X

x (-x 1 ;x 2 )

Решений нет

Решений нет