Конспект урока по алгебре в 9 классе.
Тема: Решение квадратных неравенств. Задания, сводящиеся к решению квадратных неравенств
Тип урока: закрепления знаний и способов учебных действий.
Цели урока:
1. Образовательная: формирование навыков решения квадратных неравенств на основе свойств квадратичной функции.
2. Развивающая: развитие навыков самоконтроля, взаимоконтроля, самооценки.
3. Воспитательная: воспитание взаимопонимания, взаимоуважения, чувства
ответственности.
Технологии: дифференцированное обучение, технология обучения в сотрудничестве.
Оборудование и материалы: компьютер, проектор, тесты, листы оценивания,
презентация «Решение квадратных неравенств» , карточки
Ход урока
1 этап. Организационный момент.
2 этап. Актуализация знаний. Фронтальный опрос.
Слайд 1 Урок мне хочется начать со слов персидского поэта Рудаки:
«С тех пор как существует мирозданье,
Такого нет, кто б не нуждался в знанье».
- Ребята, как вы понимаете эти строки? (Дети высказываются).
- Мы с вами тоже сегодня будем закреплять свои знания.
- Ребята, какую тему мы сейчас изучаем? (Решение квадратных неравенств).
Слайд 2
Тема: Решение квадратных неравенств. Задания, сводящиеся к решению квадратных неравенств
Цель: совершенствование навыков решения квадратных неравенств.
- Дайте определение квадратного неравенства
Слайд 3 (Неравенства вида ах2 + вх + с 0 и ах2 + вх + с
ах2 + вх + с 0
ах2 + вх + с
- Выберите из данных неравенств – квадратные
Слайд 4
1) х2 + 2х – 48
2) х2 – 6 ≤ 0 7) 3х - 17 х2 0
3) 7х + 2 х2 4 8) 5х2 –у 9
4) х – 3 0 9) - 3 х2 -6х + 9
5) – 20 х2 ≤ 5 3
- Почему не назвали 4 и 8 ? (4 – линейное неравенство, 8 – с двумя переменными).
-Что называется решением квадратного неравенства ?
(Решением квадратного неравенства называется значение переменной, которое обращает его в верное числовое неравенство).
-Что может быть решением квадратного неравенства ?
(Промежуток, число, пустое множество).
Слайд 5
Решение неравенства
Промежуток Пустое множество
Число
-Что значит - решить неравенство?
(Решить неравенство – значит найти все его решения или доказать, что их нет).
-Какие неравенства называются равносильными?
(Неравенства, имеющие одни и те же решения, называются равносильными. Неравенства, не имеющие решений, также считаются равносильными).
-Вспомним алгоритм решения квадратного неравенства.
(Учащиеся говорят, на слайде появляются шаги алгоритма).
Слайд 6.
Алгоритм
решения квадратного неравенств
1. Привести неравенство к виду ах2 + вх + с 0 (ах2 + вх + с
2. Ввести функцию f (х) = ах2 + вх + с и охарактеризовать её.
3. Найти нули функции, т.е. решить уравнение f (х) = 0.
4. Отметить на оси х нули функции и изобразить схематически параболу.
5. Отметить промежутки, которые будут являться решениями данного неравенства
(внимательно смотреть знак неравенства).
6. Записать ответ.
-Молодцы!
3 этап. Проверка домашнего задания.
А теперь проверим домашнее задание. Поменяйтесь, пожалуйста, тетрадями.
Ответы на слайде. (Взаимопроверка в парах)
Слайд 7
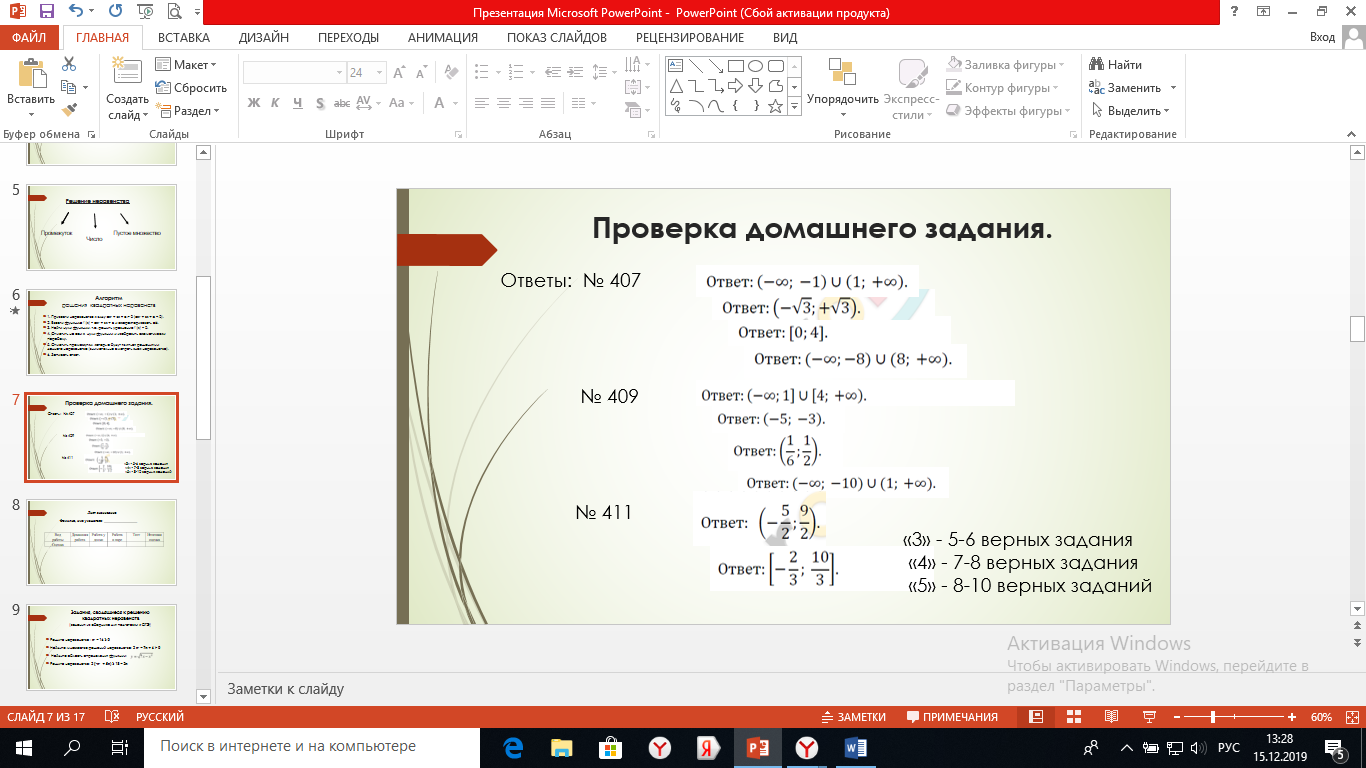
Поставьте оценки в листы оценивания.
Слайд 8 Лист оценивания
Фамилия, имя учащегося: __________________
| Вид работы | Домашняя работа | Работа у доски | Работа в паре | Тест | Итоговая оценка |
| Оценка | |
| | |
|
4 этап. Решение тренировочных упражнений. Работа на доске и в тетрадях.
Слайд 9. Лист № 1
Рассмотрим задания из сборника для подготовки к ОГЭ и решим их.
1. Решите неравенство: х2 – 16 ≥ 0

2. Найдите множество решений неравенства: 2 х2 – 7х + 6 0

3. Найдите область определения функции: 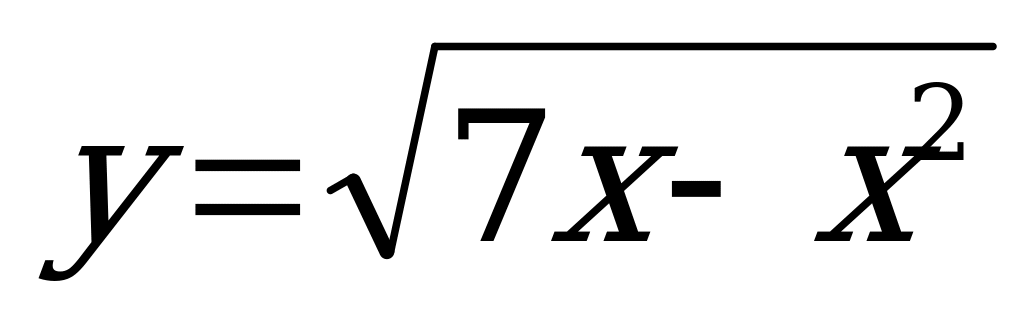



4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х

Молодцы! Справились с заданием!
Слайд 10 Работа в парах.
А сейчас, ребята, вы побываете в роли учителя. Проверьте работу ученика 9кл., находящуюся на листе № 2. Ошибки подчеркните.
Слайд 11.
Лист № 2.
№ 1. Решите неравенство: х2 – 5х + 6
f(х) = х2 – 5х + 6 – квадратичная функция, график – парабола,
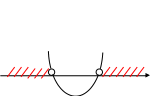 ветви вверх.
ветви вверх.
х2 – 5х + 6 = 0
х1 = 2 х2 = 3
2 3 x
Ответ: ( 2; 3 )
№ 2. Найдите множество решений неравенства:
- 0,2 х2 + х – 1,2 ≤ 0
f(х) = - 0,2 х2 + х – 1,2 - квадратичная функция, график – парабола,
ветви вниз.
- 0,2 х2 + х – 1,2 = 0 / * ( - 5)
 х2 – 5х + 6 = 0
х2 – 5х + 6 = 0
х1 = 2 х2 = 3






2 3 x
Ответ: ( -∞; 2 ) U  ( 3; + ∞)
( 3; + ∞)
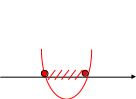
№ 3. Решите неравенство: 2х х2
2х - х2 0
f(х) = 2х - х2 - квадратичная функция, график – парабола,
ветви вниз.
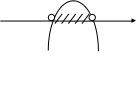 2х - х2 = 0
2х - х2 = 0
х ( 2 – х ) = 0
х = 0 или х = 2
0 2 x
Ответ: [ 0; 2 ]
№ 4. Найдите множество решений неравенства:
1 + 2х + х2 0
f(х) = 1 + 2х + х2 - квадратичная функция, график – парабола,
 ветви вниз.
ветви вниз.
1 + 2х + х2 = 0
х2 + 2х +1 = 0
х = - 1
-1 x
Ответ: - 1
Внимание на слайд! Посчитайте количество верно найденных ошибок. На слайде они выделены красным цветом.
Критерии оценки: «3» - 3-4 найденных ошибки
«4» - 5-6 найденных ошибок
«5» - 7 найденных ошибок
Поставьте оценку в свой лист оценивания.
Слайд 12 5 этап. Контроль знаний.
Тестирование с последующей взаимопроверкой.
Лист № 3
Тест. 1 вариант.
1. На каком рисунке изображено множество решений неравенства х2 – 9 ≤ 0 ?
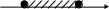
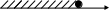 а) б)
а) б)
-3 3 x 3 x

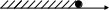 в) г)
в) г)
-3 x -3 3 x
2. Решите неравенство: х2 – 8х + 15 0
а) ( 3; 5) б) [ 3; 5 ]
в) (- ∞; 3) U (5; + ∞) г) (- ∞; 3 ] U [ 5; + ∞)
3. Найдите множество решений неравенства: 5х - х2 ≥ 0
а) [ 0; 5] б) (- ∞; 0) U (5; + ∞)
в) (- 5; 0) г) (- ∞; 0 ] U [5; + ∞)
4. Решите неравенство: 6а 2 + 10
а) ( - 4; + ∞) б) решений нет
в) ( - ∞; 4) U (36; + ∞) г) ( - ∞; + ∞ )
5. Найти область определения функции: у = 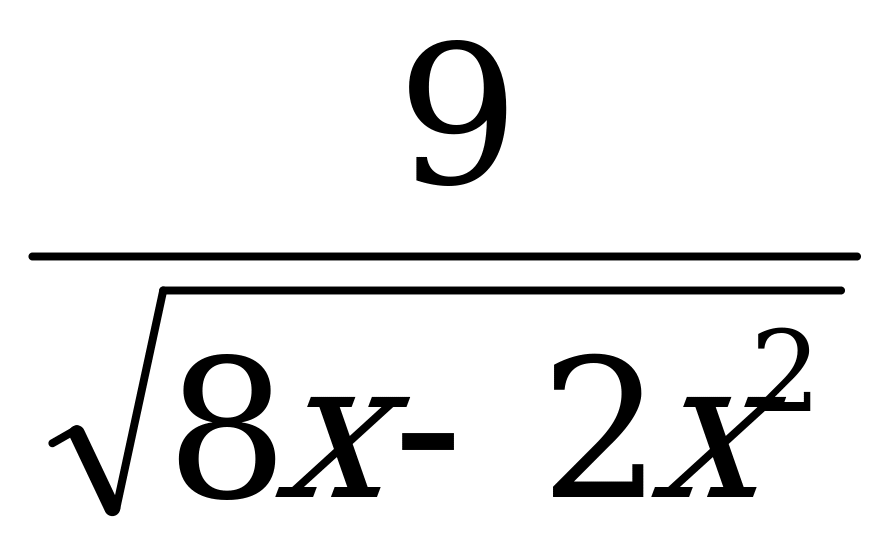
а) (- ∞; 0) U (4; + ∞) б) (0; 4)
в) (- ∞; 8 ] U [2; + ∞) г) [ 0; 4 ]
Тест. 2 вариант.
1. На каком рисунке изображено множество решений неравенства х2 – 49 ≥ 0 ?

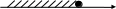 а) б)
а) б)
-7 7 x 7 x
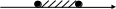
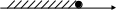 в) г)
в) г)
-7 7 x -7 x
2. Решите неравенство: х2 – 10х + 21
а) (- ∞; 3) U (7; + ∞) б) (- ∞; 3 ] U [7; + ∞)
в) [ 3; 7 ] г) ( 3; 7)
3. Найдите множество решений неравенства: 2х - х2 ≤ 0
а) (- ∞; 0 ] U [2; + ∞) б) [0; 2]
в) (0; 2) г) (- ∞; 0 ] U [2; + ∞)
4. Решите неравенство: 8в – 17 2
а) ( - 4; + ∞) б) ( - ∞; + ∞ )
в) ( - ∞; 4) U (64; + ∞) г) решений нет
5. Найти область определения функции: у = 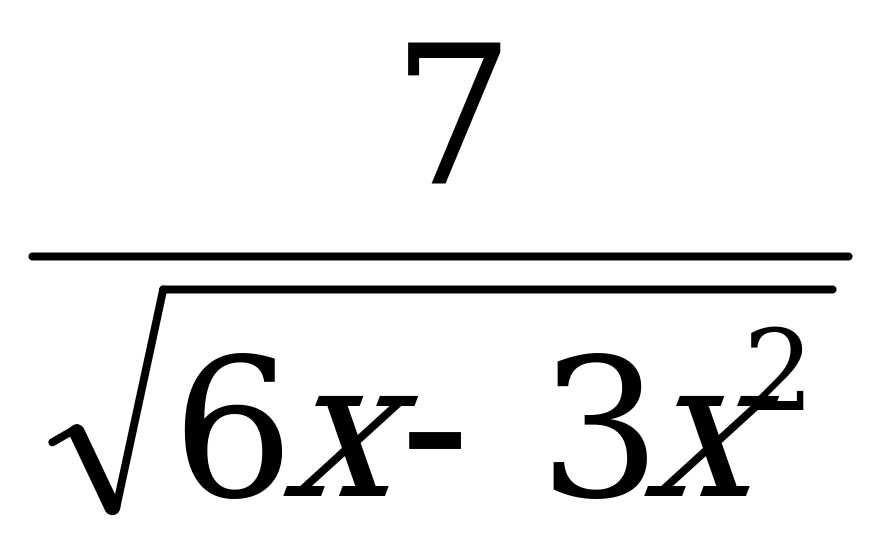
а) (- ∞; - 3] U [6; + ∞) б)(- ∞; 0) U (2; + ∞)
в) (0; 2) г) [ 0; 2 ]
Слайд 13. Проверяем соседа
1 вариант. 2 вариант.
а а
в г
а а
г б
б в
Критерии оценки: «3» - 3 верных задания
«4» - 4 верных задания
«5» - 5 верных заданий
Поставьте оценки в листы оценивания.
6 этап. Обобщение (устно)
Итак, сегодня мы решили много различных заданий. Решение каждой задачи сводилось к решению квадратного неравенства на основе свойств квадратичной функции. Ребята, у меня к вам вопрос.
Слайд 14.
х2 – 12х + 35
Какие задачи можно составить с квадратным трехчленом х2 – 12х + 35, чтобы при их решении возникла необходимость решить квадратное неравенство ?
1. Решите неравенство …
2. Найдите множество решений неравенства …
3. Найдите область определения функции …
4. При каких значениях х квадратный трехчлен принимает положительные (отрицательные) значения).
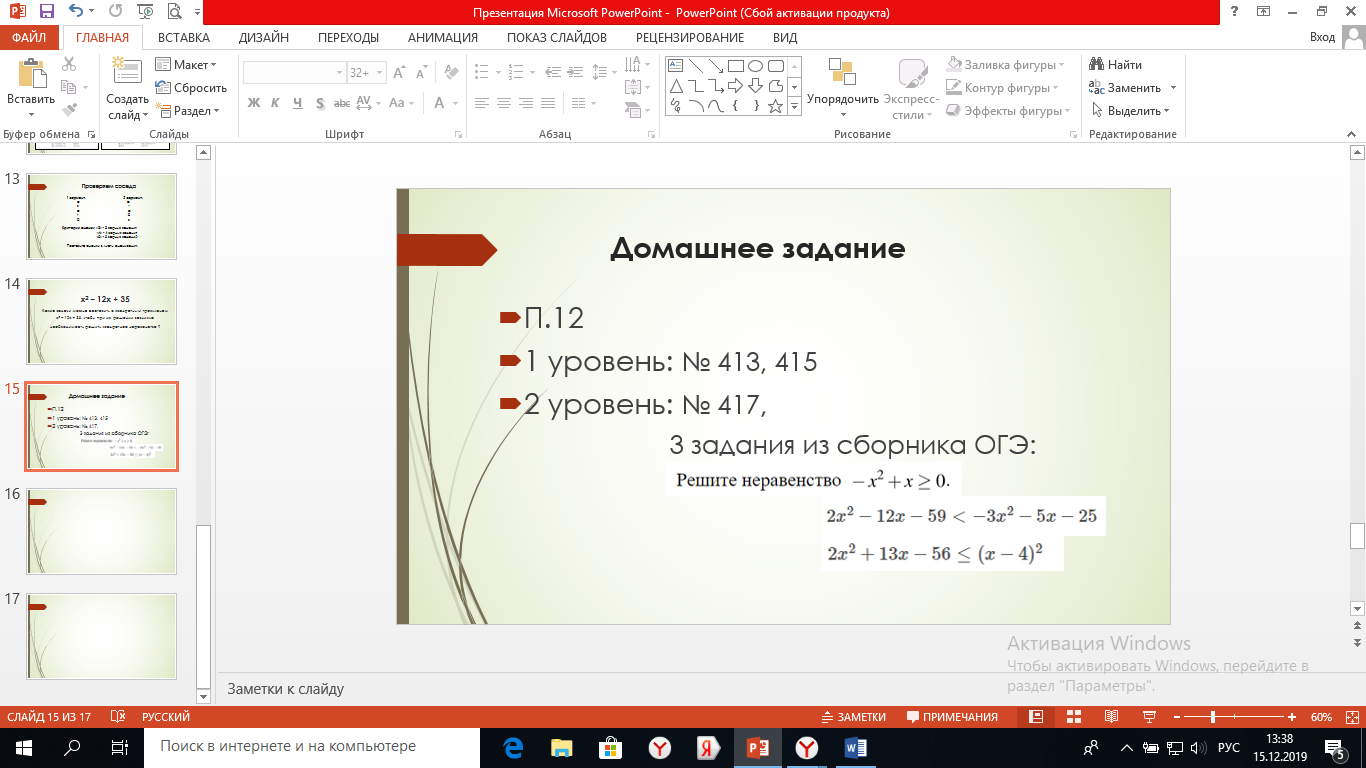
Слайд 15 Домашнее задание.
Выберите, пожалуйста, домашнее задание и запишите
Слайд 16 Рефлексия.
Ребята, какая цель стояла сегодня перед вами?
Цель: совершенствование навыков решения квадратного неравенств
Как вы считаете достигнута ли она?
-
На уроке я работал… -
Своей работой на уроке я… -
Урок для меня показался… -
За урок я… -
Моё настроение… -
Материал урока мне был…
7. Домашнее задание мне кажется… | -
Активно/пассивно -
Доволен/недоволен -
Коротким/длинным -
Не устал/ устал -
Стало лучше/ стало хуже -
Понятен /не понятен полезен / бесполезен интересен/неинтересен 7. Легким/ трудным |
Молодцы! Сегодня все работали очень хорошо! Ребята, каждый из вас индивидуален и неповторим. Я всех благодарю за работу.
Лист оценивания
Фамилия, имя учащегося: __________________
| Вид работы | Домашняя работа | Работа у доски | Работа в паре | Тест | Итоговая оценка |
| Оценка | |
| | |
|
Лист оценивания
Фамилия, имя учащегося: __________________
| Вид работы | Домашняя работа | Работа у доски | Работа в паре | Тест | Итоговая оценка |
| Оценка | |
| | |
|
Лист оценивания
Фамилия, имя учащегося: __________________
| Вид работы | Домашняя работа | Работа у доски | Работа в паре | Тест | Итоговая оценка |
| Оценка | |
| | |
|
Лист оценивания
Фамилия, имя учащегося: __________________
| Вид работы | Домашняя работа | Работа у доски | Работа в паре | Тест | Итоговая оценка |
| Оценка | |
| | |
|
Лист оценивания
Фамилия, имя учащегося: __________________
| Вид работы | Домашняя работа | Работа у доски | Работа в паре | Тест | Итоговая оценка |
| Оценка | |
| | |
|
Лист № 3
Тест. 1 вариант.
1. На каком рисунке изображено множество решений неравенства х2 – 9 ≤ 0 ?
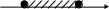
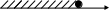 а) б)
а) б)
-3 3 x 3 x

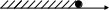 в) г)
в) г)
-3 x -3 3 x
2. Решите неравенство: х2 – 8х + 15 0
а) ( 3; 5) б) [ 3; 5 ]
в) (- ∞; 3) U (5; + ∞) г) (- ∞; 3 ] U [ 5; + ∞)
3. Найдите множество решений неравенства: 5х - х2 ≥ 0
а) [ 0; 5] б) (- ∞; 0) U (5; + ∞)
в) (- 5; 0) г) (- ∞; 0 ] U [5; + ∞)
4. Решите неравенство: 6а 2 + 10
а) ( - 4; + ∞) б) решений нет
в) ( - ∞; 4) U (36; + ∞) г) ( - ∞; + ∞ )
5. Найти область определения функции: у = 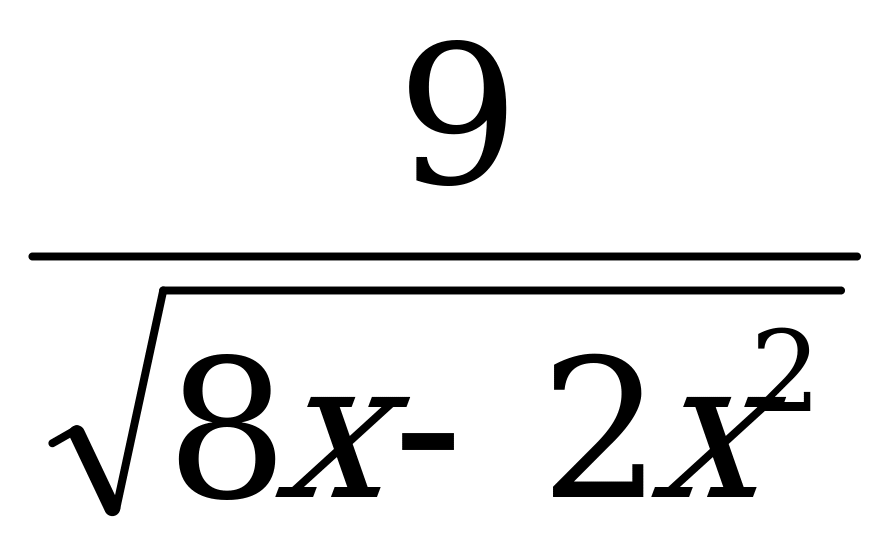
а) (- ∞; 0) U (4; + ∞) б) (0; 4)
в) (- ∞; 8 ] U [2; + ∞) г) [ 0; 4 ]
Лист № 3
Тест. 2 вариант.
1. На каком рисунке изображено множество решений неравенства х2 – 49 ≥ 0 ?

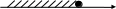 а) б)
а) б)
-7 7 x 7 x
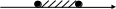
 в) г)
в) г)
-7 7 x -7 x
2. Решите неравенство: х2 – 10х + 21
а) (- ∞; 3) U (7; + ∞) б) (- ∞; 3 ] U [7; + ∞)
в) [ 3; 7 ] г) ( 3; 7)
3. Найдите множество решений неравенства: 2х - х2 ≤ 0
а) (- ∞; 0 ] U [2; + ∞) б) [0; 2]
в) (0; 2) г) (- ∞; 0 ] U [2; + ∞)
4. Решите неравенство: 8в – 17 2
а) ( - 4; + ∞) б) ( - ∞; + ∞ )
в) ( - ∞; 4) U (64; + ∞) г) решений нет
5. Найти область определения функции: у = 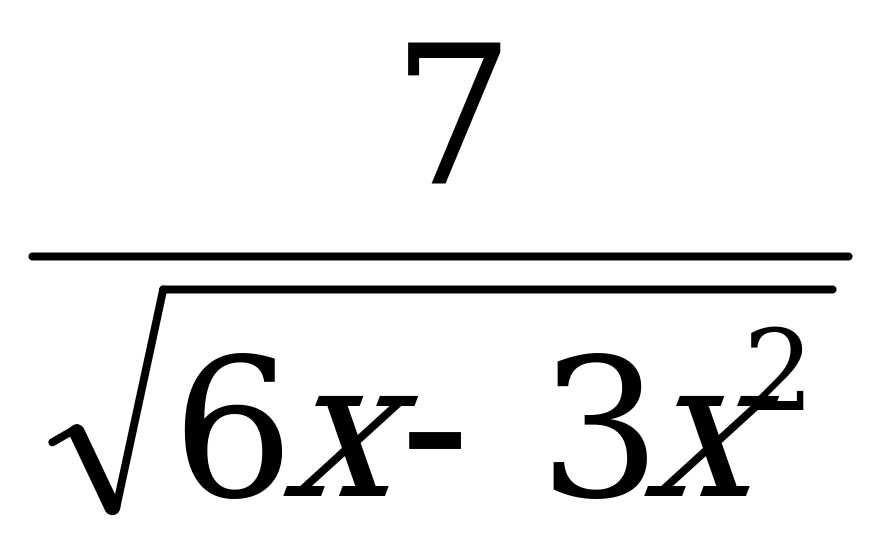
а) (- ∞; - 3] U [6; + ∞) б)(- ∞; 0) U (2; + ∞)
в) (0; 2) г) [ 0; 2 ]
Лист № 1
Рассмотрим задания из сборника для подготовки к ОГЭ и решим их.
1. Решите неравенство: х2 – 16 ≥ 0
2. Найдите множество решений неравенства: 2 х2 – 7х + 6 0
3. Найдите область определения функции: 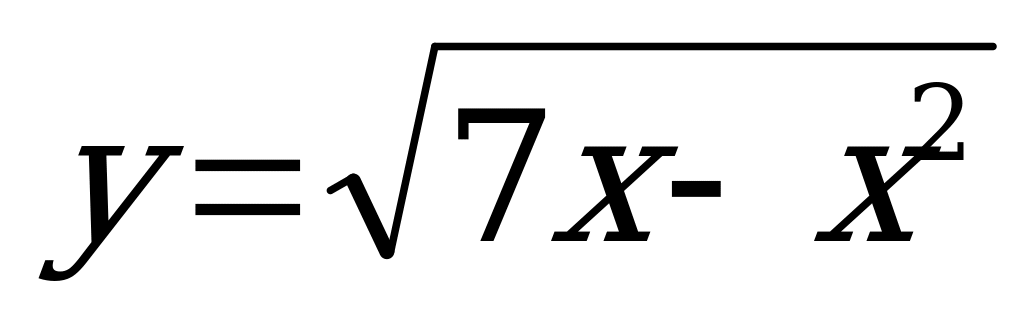
4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
Лист № 1
Рассмотрим задания из сборника для подготовки к ОГЭ и решим их.
1. Решите неравенство: х2 – 16 ≥ 0
2. Найдите множество решений неравенства: 2 х2 – 7х + 6 0
3. Найдите область определения функции: 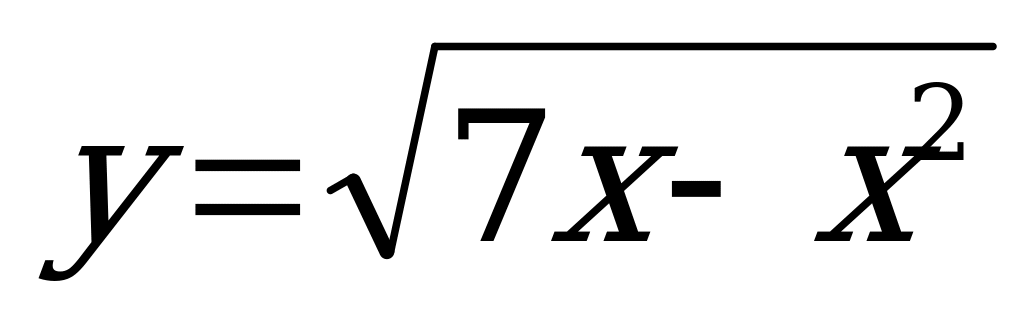

 4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
Лист № 1
Рассмотрим задания из сборника для подготовки к ОГЭ и решим их.
1. Решите неравенство: х2 – 16 ≥ 0
2. Найдите множество решений неравенства: 2 х2 – 7х + 6 0
3. Найдите область определения функции: 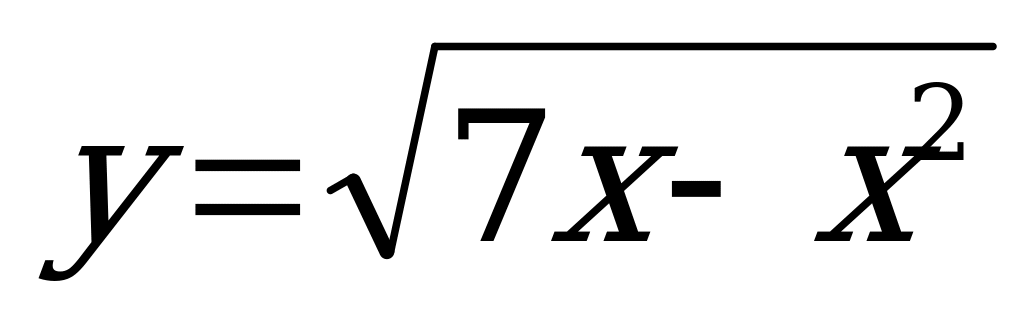

 4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
Лист № 1
Рассмотрим задания из сборника для подготовки к ОГЭ и решим их.
1. Решите неравенство: х2 – 16 ≥ 0
2. Найдите множество решений неравенства: 2 х2 – 7х + 6 0
3. Найдите область определения функции: 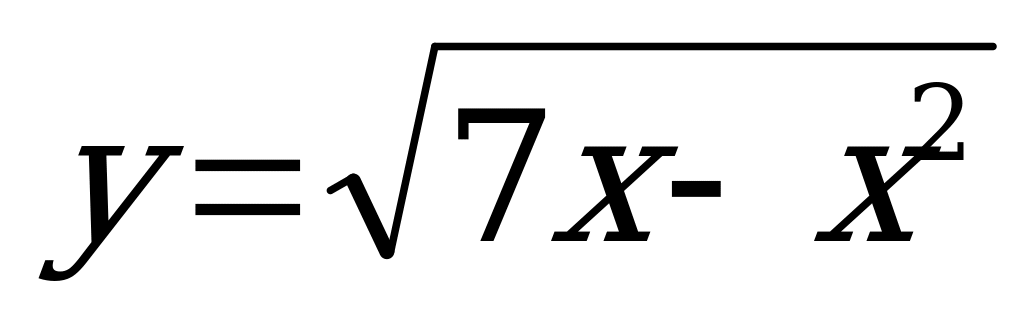

 4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
Лист № 1
Рассмотрим задания из сборника для подготовки к ОГЭ и решим их.
1. Решите неравенство: х2 – 16 ≥ 0
2. Найдите множество решений неравенства: 2 х2 – 7х + 6 0
3. Найдите область определения функции: 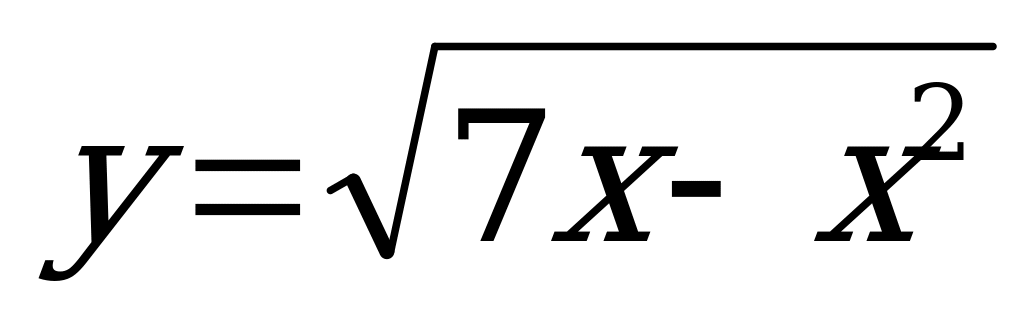

 4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
Лист № 1
Рассмотрим задания из сборника для подготовки к ОГЭ и решим их.
1. Решите неравенство: х2 – 16 ≥ 0
2. Найдите множество решений неравенства: 2 х2 – 7х + 6 0
3. Найдите область определения функции: 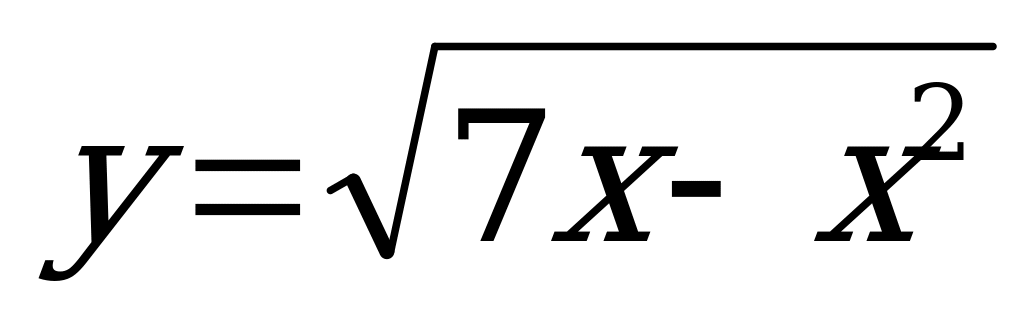

 4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х
4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х












 ветви вверх.
ветви вверх. х2 – 5х + 6 = 0
х2 – 5х + 6 = 0

 ( 3; + ∞)
( 3; + ∞) 2х - х2 = 0
2х - х2 = 0 ветви вниз.
ветви вниз.
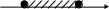
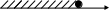 а) б)
а) б)
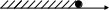 в) г)
в) г) 
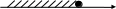 а) б)
а) б) 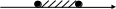
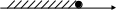 в) г)
в) г)





















