Россия, Симферополь
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 19.03.2025 19:34
Живогляд Дарья Владимировна
Учитель математики
17 468
1 906 
Местоположение
Специализация
Решение линейных неравенств с одной переменной
Категория:
Алгебра
29.03.2020 17:32
Просмотр содержимого документа
«Решение линейных неравенств с одной переменной»
Дата 30.03.2020
Тема: РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ
Задачи: повторить понятия «числовой промежуток» и «неравенство с одной переменной», их запись и изображение; научиться решать линейные неравенства с одной переменной.
Ход урока
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Продолжаем изучать раздел «Неравенства с одной переменной и их свойства». Откройте свои тетради и запишите сегодняшнее число и тему урока «Решение неравенств с одной переменной».
Прежде чем перейти к изучению нового материала повторим всю необходимую теорию.
1.1. Ответьте на вопросы устно.
1. Что называется множеством?
2. Как найти объединение двух множеств? Пересечение двух множеств?
3. Какие числовые промежутки мы изучили?
4. Какие неравенства называются строгими? Нестрогими?
5. Почему некоторые точки на числовой прямой закрашены, а другие нет? От чего это зависит?
1.2. Реши устно. Найти объединение и пересечение двух множеств:
а) А={1; 4; 5; 11; 16; 17}, B={1; 2; 3; 4; 11; 13; 15; 17};
б) А=[ -4; 5]; B=[0; 3].
1.3. Верно ли выполнено задание
Найти объединение и пересечение множеств А=[-2; 3) и В=(1; 5].
Выполним соответствующий рисунок.
А∩В=[-2; 3)∩(1; 5] = (1; 3).
А∩В=[-2; 3)U(1; 5] = [-2; 5].
Кто не справился с устными заданиями, откройте учебники на странице 183 и повторите необходимый материал, записанный в виде таблицы.
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Рассмотрим общий вид линейного неравенства и случаи его решения. Для вывода алгоритма решения неравенства будем использовать строгие знаки ( и
Неравенство вида ax + b0 ( может быть любой из четырех возможных знаков , ≥, линейным неравенством с одной переменной. Заметим, что левая часть линейного неравенства является линейной функцией. В правой части неравенства не всегда будет 0, возможны различные выражения. Но равносильными преобразованиями мы можем прийти к нулю.
Алгоритм решения линейного неравенства ax + b0:
1 шаг. Перенести число b в правую часть неравенства, меняя при этом знак числа на противоположный: ax 0-b, т.е. ax -b.
2 шаг. Необходимо избавиться от множителя а в левой части, разделив каждую часть неравенства на число а. НО! ВАЖНО. Число а может быть положительным или отрицательным, это влияет на смену знака самого неравенства.
Если a0, то знак неравенства не меняется. Получим
Изобразим это решение на числовой прямой и получим ответ 
.
Если a, то знак самого неравенства меняется на противоположный. Получим
Изобразим это решение на числовой прямой и получим ответ 
.
Алгоритм решения линейных неравенств напоминает алгоритм решения линейных уравнений. В одной части должны быть выражения с неизвестными, а в другой – числа без неизвестных.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Пример 1. Решим неравенство 8х ≤ 3х + 15.
Перенесем слагаемое 3х с противоположным знаком в левую часть неравенства: 8х - 3х ≤ 15. Приведем подобные члены: 5х ≤ 15. Разделим обе части неравенства на положительное число 5 (при этом знак неравенства сохраняется) и получаем х ≤ 3. Множество решений данного неравенства состоит из чисел, которые меньше или равны числу 3. Такое множество представляет собой числовой промежуток (-∞; 3], изображенный на рисунке.
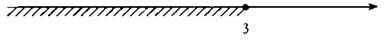
Пример 2. Решим неравенство 3(2х - 1) 2(х + 2) + х + 5.
Раскроем скобки в обеих частях неравенства: 6х – 3 2х + 4 + х + 5. Приведем в правой части подобные члены: 6x – 3 3x + 9. Перенесем с противоположным знаком член 3х из правой части в левую, а член -3 из левой части в правую 6х - 3х 9 + 3. Опять приведем подобные члены в обеих частях неравенства: 3х 12. Разделим обе части неравенства на положительное число 3 (при этом знак неравенства сохраняется) и получаем х 4. Множество решений данного неравенства состоит из всех чисел, больших 4. Такое множество представляет собой промежуток (4; +∞), изображенный на рисунке.
Выполните задания по учебнику №836(а-г), №840(а-г).
Если у вас возникают вопросы по решению, задавайте их сразу.
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Неравенства какого вида называются линейными?
Как найти решение линейного неравенства?
Домашнее задание: №837(а-г).
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
