Решение неравенств методом интервалов

Муниципальное бюджетное общеобразовательное учреждение

города Керчи Республики Крым

«Специализированная школа №19 с углубленным изучением

английского языка

Решение неравенств методом интервалов

урок алгебры в 9 классе

Учитель Васильева О.В.

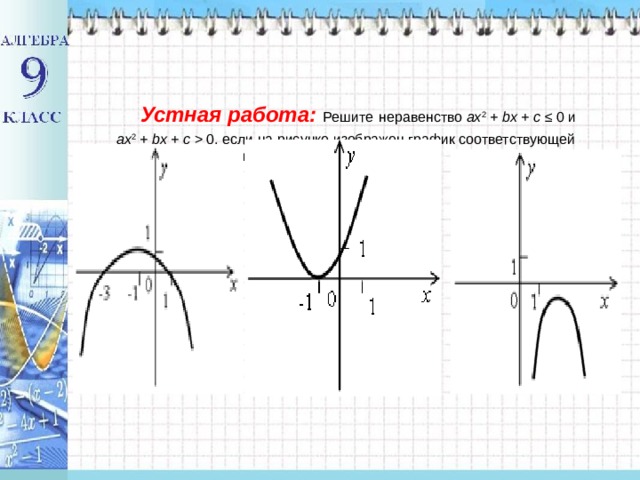0, если на рисунке изображен график соответствующей квадратичной функции: " width="640"

Устная работа : Решите неравенство ах 2 + bx + c ≤ 0 и ах 2 + bx + c 0, если на рисунке изображен график соответствующей квадратичной функции:

0; в) 9 – х 2 1-В а р и а н т Решите неравенство : а) х 2 – 8 х + 15 0; б) 2 х – х 2 ≥ 0; в) х 2 + 2 х + 1 0. " width="640"

Проверочная работа

2-В а р и а н т

Решите неравенство :

а) х 2 – 10 х + 21 ≤ 0;

б) х 2 – 10 х + 25 0;

в) 9 – х 2

1-В а р и а н т

Решите неравенство :

а) х 2 – 8 х + 15 0;

б) 2 х – х 2 ≥ 0;

в) х 2 + 2 х + 1 0.

План применения метода интервалов

!

• Разложить многочлен на простые множители;
• найти корни многочлена;
• изобразить их на числовой прямой;
• разбить числовую прямую на интервалы;
• определить знаки множителей на интервалах знакопостоянства;
• выбрать промежутки нужного знака;
• записать ответ (с помощью скобок или знаков неравенства).

1

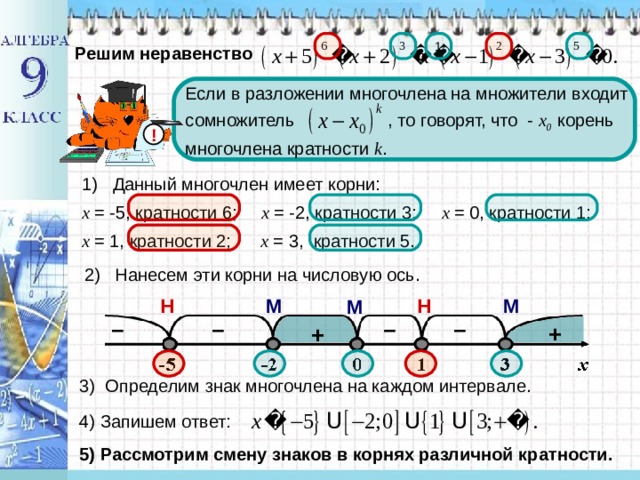
Решим неравенство

Если в разложении многочлена на множители входит сомножитель , то говорят, что - х 0 корень многочлена кратности k .

!

1) Данный многочлен имеет корни:

x = -5, кратности 6; x = -2, кратности 3; x = 0, кратности 1;

x = 1, кратности 2; x = 3, кратности 5.

2) Нанесем эти корни на числовую ось.

Н

М

М

Н

М

–

–

–

–

+

+

3) Определим знак многочлена на каждом интервале .

4) Запишем ответ:

5) Рассмотрим смену знаков в корнях различной кратности.

Решите неравенство

1 вариант:

2 вариант:

Сделайте выводы о смене знака на интервалах, в зависимости от степени кратности корня.

Обобщая ваши наблюдения, делаем выводы:

Для решения неравенства важно знать, является ли k четным или нечетным числом.

1

При четном k многочлен справа и слева от х 0 имеет один и тот же знак

( знак многочлена не меняется ).

2

При нечетном k многочлен справа и слева от х 0 имеет противоположные знаки

( знак многочлена изменяется ).

• При нечетном k многочлен справа и слева от х 0 имеет противоположные знаки ( знак многочлена изменяется ).

3

Решение рациональных неравенств

Умножим обе части такого неравенства на многочлен

Знак исходного неравенства не меняется, (т.к ).

Получаем неравенство , равносильное данному неравенству, которое решаем методом интервалов.

Итак:

Решение рациональных неравенств равносильно решению системы:

!

Решим неравенство

1) Найдем область определения неравенства:

откуда

2) Сведем данное рациональное неравенство к алгебраическому, умножив неравенство на квадрат знаменателя:

3) Находим корни многочлена и определяем их кратность:

х =1 (четная кратность), корни 3, -1, 0, 5, -2 (нечетная кратность).

М

М

Н

М

М

М

–

–

–

+

+

–

+

-2

3

-1

1

0

5

x

4 ) Определим знак многочлена при х = 10, и расставим остальные знаки с учетом кратности корней .

5 ) Запишем ответ:

Фронтальная работа с классом 

№ 389 (а, в),

№ 390 (в, г),

№ 393(а),

№ 394(а).

!

Домашнее задание.

Повторить §15 (глава II ),

№ 389 (б), № 390 (б), №393(б), №394(б).

!

Рефлексия.

1. В чем состоит метод интервалов решения неравенств?

!

2. Любое ли неравенство можно решить методом интервалов?

3.  Как применяется метод интервалов к решению дробных неравенств?

4. Как решается неравенство, содержащее целое выражение выше второй степени?