Россия, г.Углегорск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 23.05.2025 14:25
Чернова Людмила Васильевна
Учитель математики
70 лет
952
62 590 
Местоположение
Специализация
Решение неравенств второй степени с одной переменной.
Категория:
Математика
19.03.2019 11:41
Просмотр содержимого документа
«Решение неравенств второй степени с одной переменной.»
Девиз урока
- Правильному применению методов можно научиться только применяя их на разнообразных примерах. (Г. Цейтен)
Повторение
1 . Выражение какого вида называется квадратным трёхчленом?
2 . Что надо сделать, чтобы найти корни квадратного трёхчлена?
Надо квадратный трёхчлен приравнять к нулю и решить уравнение
0, то ветви вверх, если a " width="640"
Повторение
- Как называется функция вида у = ах 2 +вх + с ?
Квадратичной
2. Что является графиком квадратичной функции?
Парабола
3. От чего зависит направление ветвей?
От коэффициента а,
если а 0, то ветви вверх, если a
Проверь себя
1.
Знак коэффициента а
а
б
+
Число корней
+
в
2
0
г
-
-
д
2
0
е
+
-
1
1
г
а
д
б
е
в
Цель урока
- Знать определение неравенств второй степени с одной переменной.
- Уметь решать неравенства второй степени с одной переменной графическим способом.
Решение неравенств
второй степени
с одной
переменной
0 и ах 2 + вх + с 2.где х - переменная, 3. а, в, с –некоторые числа, 4.причем а ≠0 , " width="640"
Определение неравенства второй степени с одной переменной
1.Какой вид имеет неравенство второй степени с одной переменной?
2.Что такое х ?
3.Что такое a,b,c?
4.Какие ограничения для коэффициента а?
1.Неравенства вида
ах 2 + вх + с 0 и
ах 2 + вх + с
2.где х - переменная,
3. а, в, с –некоторые числа,
4.причем а ≠0 ,
0, y 2 1 3 4 5 " width="640"
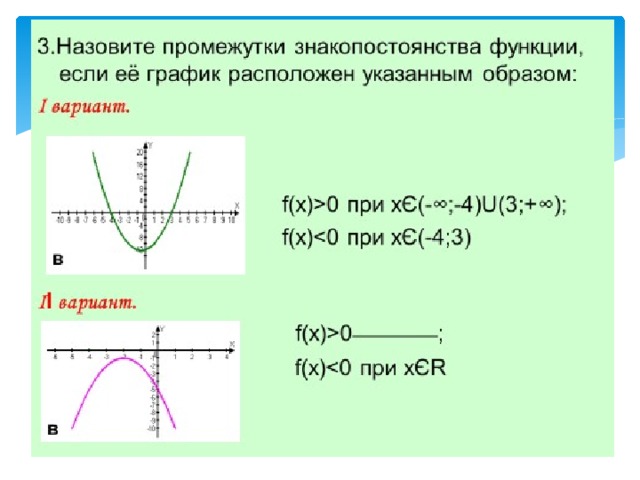
По схеме определите знаки коэффициентов a, b, c и D.
Назовите промежутки, при которых y 0, y
2
1
3
4
5
1. Найдем корни квадратного трехчлена :
х 2 - 7х + 10 = 0
Д = 9
х 1 = 2
х 2 = 5
2. Рассмотрим функцию:
у = х 2 - 7х + 10
- Графиком этой функции является
- парабола
- «Ветви» параболы направлены
- вверх
- Парабола пересекает ось х в двух точках
2 и 5
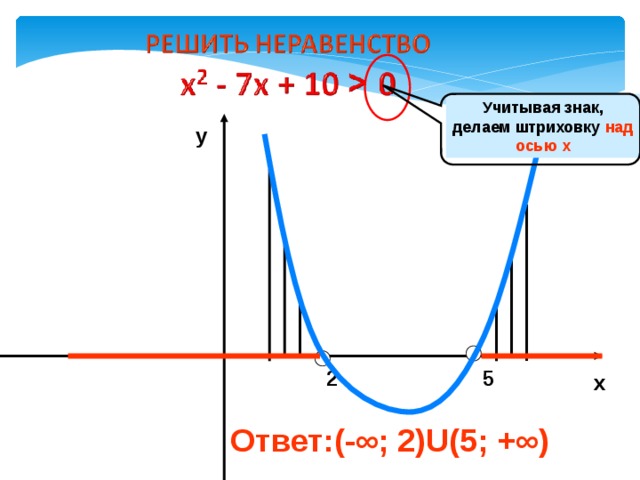
Учитывая знак, делаем штриховку над осью х
у
5
2
х
Ответ:(-∞; 2)U(5; +∞)
![Решить неравенство - х 2 - 3х + 4 ≥ 0 у 1.Найдем корни квадратного трехчлена -х 2 - 3х + 4 = 0 х 1 = - 4 х 2 = 1 2. «Ветви» параболы направлены Вниз Парабола проходит через точки - 4 и 1 Учитывая знак неравенства, делаем штриховку над осью х - 4 1 х Ответ: [- 4; 1]](https://fsd.multiurok.ru/html/2019/03/19/s_5c90aaf4b6364/img11.jpg)
Решить неравенство
- х 2 - 3х + 4 ≥ 0
у
1.Найдем корни квадратного трехчлена
-х 2 - 3х + 4 = 0
х 1 = - 4 х 2 = 1
2. «Ветви» параболы направлены
Вниз
- Парабола проходит через точки
- 4 и 1
Учитывая знак неравенства, делаем штриховку над осью х
- 4
1
х
Ответ: [- 4; 1]
0 1 ) Решим уравнение х 2 – 3х + 4 = 0 Д = - 7 Корней нет 2)Графиком является парабола «Ветви» параболы направлены вверх х ОТВЕТ: Х – ЛЮБОЕ ЧИСЛО Или " width="640"
Учитываем знак
у
Решить неравенство
х 2 – 3х + 4 0
1 ) Решим уравнение
х 2 – 3х + 4 = 0
Д = - 7
Корней нет
2)Графиком является
парабола
«Ветви» параболы направлены
вверх
х
ОТВЕТ: Х – ЛЮБОЕ ЧИСЛО
Или
0 и ax 2 + в x + c надо: Найти дискриминант квадратного трехчлена и его корни Отметить корни на оси х Через отмеченные точки провести параболу , ветви которой направлены - вверх, если а 0, - вниз, если a 4. Если корней нет, то параболу изобразить в верхней полуплоскости при а 0 в нижней полуплоскости при а 0 Для неравенства ах 2 + вх + с 0 сделать штриховку над осью х Для неравенства ах 2 + вх + с 7. Заштрихованные промежутки записать в ответ " width="640"
План решения неравенств второй степени
Чтобы решить неравенства вида
ах 2 + вх + с 0 и ax 2 + в x + c надо:
- Найти дискриминант квадратного трехчлена и его корни
- Отметить корни на оси х
- Через отмеченные точки провести параболу , ветви которой направлены
- вверх, если а 0,
- вниз, если a
4. Если корней нет, то параболу изобразить
в верхней полуплоскости при а 0
в нижней полуплоскости при а 0
- Для неравенства ах 2 + вх + с 0 сделать штриховку над осью х
- Для неравенства ах 2 + вх + с
7. Заштрихованные промежутки записать в ответ
0 a0 D=0 aD " width="640"
D0
a0
D=0
a
D
Анализируем урок
Сегодня я узнал …
Было трудно …
Было интересно …
Я понял, что…
Теперь я могу …
Я попробую …
Я научился …
Меня заинтересовало …
Меня удивило …
Спасибо всем за урок!
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
