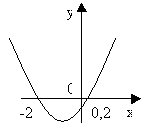Украина, Донецк
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 24.05.2025 15:10
Горкуша Виктория Александровна
Учитель математики
46 лет
633
84 410 
Местоположение
Решение неравенства второй степени с одной переменной
Категория:
Алгебра
26.10.2021 09:52
Просмотр содержимого документа
«Решение неравенства второй степени с одной переменной»
Урок
Тема: Решение неравенства второй степени с одной переменной
Цели урока
образовательная: изучить определение неравенств второй степени с одной переменной; научиться решать неравенства второй степени с одной переменной графическим способом.
развивающая: развивать логическое мышление, математическую речь, познавательный интерес к предмету. Развивать внимание, умение выделять главное, сравнивать.
воспитательная: воспитывать прилежание, трудолюбие, аккуратность, точность. Воспитание коммуникативных навыков: умение слышать и слушать.
Тип урока: урок формирования умений и навыков
Ход урока
1. Организационный момент.
Проверка готовности класса к уроку. Сообщение темы и цели урока.
2. Проверка домашнего задания.
Ответы на вопросы возникшие при выполнении домашнего задания, разбор не решенных заданий.
3. Актуализация знаний.
Фронтальный опрос
– Какую функцию мы изучаем?
– Определение квадратичной функции.
– Давайте поработаем устно, чтобы хорошо усвоить новый материал.
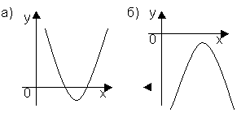
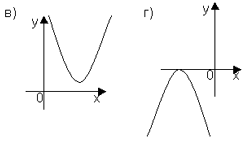
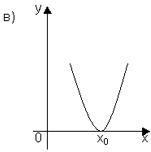
1. Определить количество корней уравнения ах2 + вх + с = 0 и знак коэффициента а, если график квадратной функции у = ах2 + вх + с расположен следующим образом:
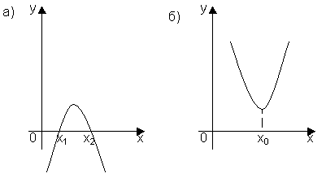
2. Укажите промежутки, в которых функция у=ах2+вх+с принимает положительные и отрицательные значения, если её график расположен указанным образом:
Постановка цели.
– Мы с вами умеем строить график квадратичной функции, умеем решать квадратные уравнения, а сегодня мы должны научиться решать неравенства второй степени с одной переменной.
Запишем тему урока в тетрадь.
4. Изучение нового материала.
Итак, какой формулой задаётся квадратичная функция?
Какой вид имеет квадратное уравнение?
Какой вид имеет квадратный трёхчлен?
Как вы думаете, какой вид будет иметь неравенство второй степени с одной переменной? ах2 + вх + с 0 и ах2 + вх + с
Попробуйте сформулировать определение.
Итак, запишем определение в тетрадь (стр.41).
Определение: Неравенствами второй степени с одной переменной называют неравенства вида ах2 + вх + с 0 и ах2 + вх + с 0, где х – переменная, а, в и с – некоторые числа, причем а ≠ 0.
Решать такие неравенства мы будем с помощью нахождения промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.
Итак, выполним в тетрадях следующее задание:
Решить неравенство: 5х2 + 9х – 2 0.
Решение.
– Какая квадратичная функция соответствует данному неравенству:
1. у = 5х2 + 9х – 2
– Что является её графиком?
– Выясним, как расположена парабола относительно оси х.
– Как она может быть расположена (пересекать ось х, находиться выше оси х, ниже оси х, касаться оси х)?
– Как это определить?
2. Нули функции, у = 0.
5х2 + 9х – 2 = 0,
D = 81 + 40 = 121,
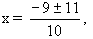
х1 = 0,2 , х2 = -2.
3. Покажем схематически, как расположена парабола в координатной плоскости.
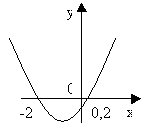
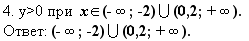
Запишем алгоритм решения неравенств второй степени с одной переменной.
1. Рассмотреть функцию, соответствующую данному неравенству, определить направление ветвей параболы.
2. Найти нули функции, т.е. абсциссы точек пересечения параболы с осью х, если они есть.
3. Изобразить схематически параболу в координатной плоскости.
4. Выбрать нужные промежутки.
5. Записать ответ.
Рассмотрим пример 3 и пример 4 в учебнике на странице 43. Сделаем соответствующие выводы.
5. Закрепление изученного материала.
Выполняем № 114 (а, в, д).
6. Обучающая самостоятельная работа.
Предлагается решить 3 неравенства, затем на доске показываются правильные ответы, для того, чтобы учащиеся могли проверить свои решения. Во время решения учащиеся консультируются с учителем. Те, кто успешно справится с решением, получат оценки.
Поднятием рук проверяем, как учащиеся усвоили новый материал.
7. Подведение итогов.
– Какова была цель нашего урока?
– Сформулируйте определение неравенств второй степени с одной переменной.
– Как решать такие неравенства?
– Алгоритм решения.
Оценки за урок.
8. Домашнее задание.
п.8, № 114(б, г, е), № 117 (предварительно нужно составить неравенство, а затем его решить).
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
