Просмотр содержимого документа
«Решение показательных и логарифмических неравенств методом рационализации»

Решение показательных и
логарифмических неравенств
методом рационализации
Учитель математики
МБУ «Школа 82»,г.о.Тольятти Самарской области
Родионова Г. М.
 0. " width="640"
0. " width="640"
Решение показательных
неравенств
Основная теорема:
Сравнение (уравнение или неравенство)
при всех допустимых значениях основания
а 0.

Решите неравенство

Решение показательного
неравенства, содержащего
переменную в основании
Из основной теоремы следует, что множитель вида
и множитель вида (а – 1)(f(x) – g(x)) при всех значениях переменных имеет один и тот же знак. Это дает возможность быстро рационализировать показательное неравенство

Решение показательных
неравенств, содержащих
переменную в основании

1. Решите неравенство
Решение:
Выражение при любом значении переменной. Поэтому можно применить алгоритм решения показательных неравенств. Несмотря на переменное основание степени.
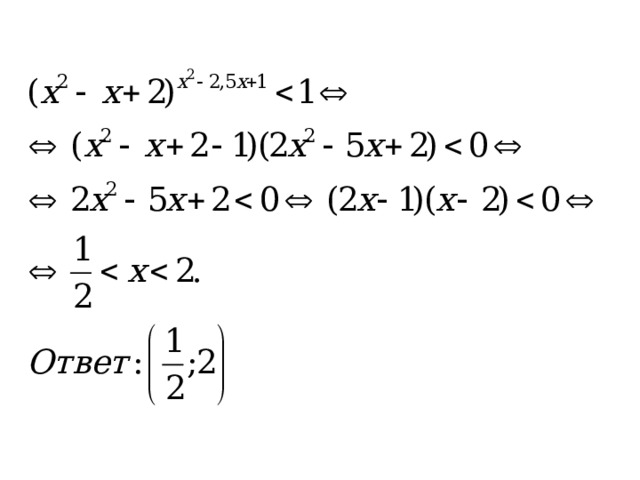

2. Решите неравенство
Решение:
Применим следствие из основной теоремы к каждому множителю. Входящему в левую часть неравенства. Так как основания степеней ,входящих в данное выражение, больше 1,то не будем в данном случае указывать соответствующий множитель (а - 1).
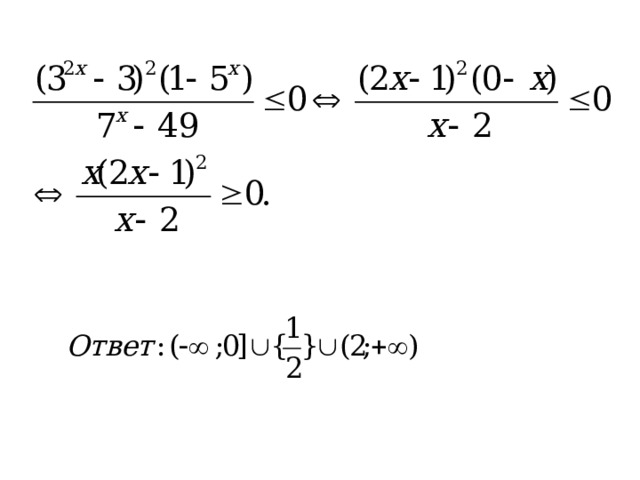

3.Решите неравенство
Заметив, что и рационализируя неравенство получим

Решение логарифмических неравенств
Основная теорема:
Для любого
Сравнение (уравнение или неравенство)

Основная теорема дает возможность решать логарифмические неравенства методом рационализации.
 0, g(x)0, разность имеет тот же знак , что и произведение " width="640"
0, g(x)0, разность имеет тот же знак , что и произведение " width="640"
Следствие . При всех допустимых значениях аргумента, т. е. при f(x)0, g(x)0, разность
имеет тот же знак , что и
произведение

Решите неравенство

Решение логарифмического
неравенства, содержащего
переменную в основании
логарифма

1. Решите неравенство

2. Решите неравенство
![Литература: ЕГЭ 2012. Математика. Решение задач. Сдаем без проблем:/ А.Р. Рязановский. В.В. Мирошин.-м. Эксэмо,2011 Решение задач и выполнение заданий по математике с комментариями и ответами для подготовки к ЕГЭ / Сост. В.Н, Студенецкая, З.С.Гребенева.- Волгоград: Учитель,2005. 3. Алгебра и начала математического анализа.10-11 классы. Задачник для учащихся общеобразовательных учреждений (профильный уровень) [А.Г. Мордкович и др].-М. Мнемозина,2009.](https://fsd.multiurok.ru/html/2022/10/05/s_633dafdc3c164/img17.jpg)
Литература:
- ЕГЭ 2012. Математика. Решение задач. Сдаем без проблем:/
А.Р. Рязановский. В.В. Мирошин.-м. Эксэмо,2011
- Решение задач и выполнение заданий по математике
с комментариями и ответами для подготовки к ЕГЭ /
Сост. В.Н, Студенецкая, З.С.Гребенева.- Волгоград:
Учитель,2005.
3. Алгебра и начала математического анализа.10-11 классы.
Задачник для учащихся общеобразовательных учреждений
(профильный уровень) [А.Г. Мордкович и др].-М. Мнемозина,2009.







 0. " width="640"
0. " width="640"




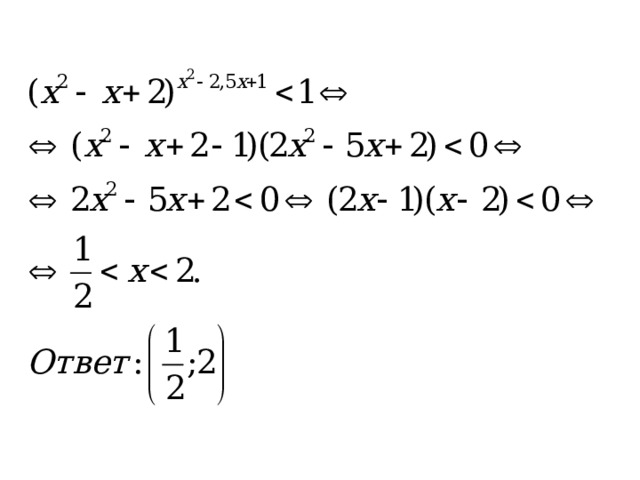

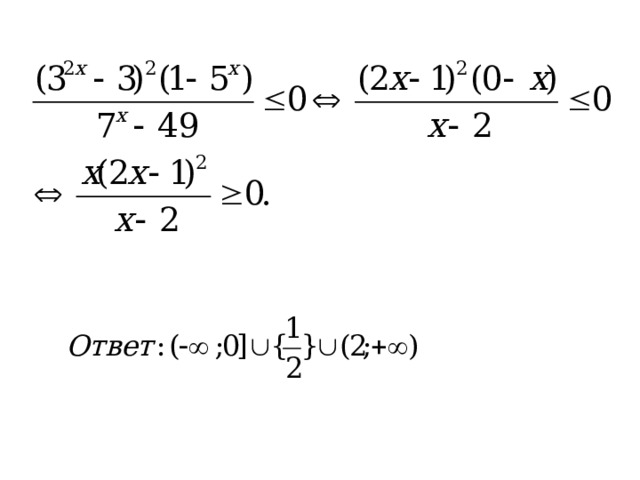



 0, g(x)0, разность имеет тот же знак , что и произведение " width="640"
0, g(x)0, разность имеет тот же знак , что и произведение " width="640"




![Литература: ЕГЭ 2012. Математика. Решение задач. Сдаем без проблем:/ А.Р. Рязановский. В.В. Мирошин.-м. Эксэмо,2011 Решение задач и выполнение заданий по математике с комментариями и ответами для подготовки к ЕГЭ / Сост. В.Н, Студенецкая, З.С.Гребенева.- Волгоград: Учитель,2005. 3. Алгебра и начала математического анализа.10-11 классы. Задачник для учащихся общеобразовательных учреждений (профильный уровень) [А.Г. Мордкович и др].-М. Мнемозина,2009.](https://fsd.multiurok.ru/html/2022/10/05/s_633dafdc3c164/img17.jpg)










