Дата проведения:
Тема урока: решение систем неравенств с одной переменной.
Класс: 8.
Тип урока: усвоение новых знаний.
Цели:
- Образовательные:
- Рассмотреть понятие системы неравенств с одной переменной.
- Дать определение решения системы неравенств с одной переменной.
- Определить, что значит решить систему неравенств.
- Научить решать системы неравенств с одной переменной.
- Воспитательные:
- Воспитание дисциплинированности.
- Воспитание интереса к изучению материала.
- Воспитание культуры общения.
- Развивающие:
- Развитие внимания, логического мышления, сообразительности.
- Развитие математической речи учащихся.
- Развитие памяти, элементов творческой деятельности.
Структура урока:
- Организационный момент
- Постановка целей и задач на урок
- Формирование новых знаний и умений
- Закрепление новых знаний и умений
- Задание на дом
- Подведение итогов
Литература: Алгебра 8 класс, Макарычев Ю.Н. и др.
Ход урока
1.Организационный момент
Приветствие , подготовка учащихся к уроку.
2.Постановка целей и задач на урок
сегодня мы с вами познакомимся с понятием систем неравенств и научимся решать.
3.Формирование новых знаний и умений
Открываем тетради, записываем число и тему сегодняшнего урока «Решение систем неравенств с одной переменной».
Давайте для начала разберем такую задачу:
Турист вышел из турбазы по направлению к станции, расположенной на расстоянии 20 км. Если турист увеличит скорость на 1 км/ч, то за 4 ч он пройдет расстояние, большее 20 км. Если он уменьшит скорость на 1 км/ч, то даже за 5 ч не успеет дойти до станции. Какова скорость туриста?
Пусть скорость туриста равна x км/ч. Если турист будет идти со скоростью (x+1) км/ч, то за 4 ч он пройдет 4(x+1) км. По условию задачи 4(x+1) > 20. Если турист будет идти со скоростью (x-1) км/ч, то за 5 ч он пройдет 5(x-1) км. По условию задачи 5(x-1) < 20.
Требуется найти те значения x , при которых верно как неравенство 4(x+1) > 20, так и неравенство 5(x-1) < 20, т.е.найти общее решение этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют запись

Заменив каждое неравенство системы равносильным ему неравенством, получим систему

Значит, значение  должно удовлетворять условию
должно удовлетворять условию
4 < x < 5.
Ответ: скорость туриста больше 4 км/ч, но меньше 5 км/ч.
Итак. Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.
Решить неравенство – значит найти все его решения или доказать, что решений нет.
Давайте сейчас рассмотрим, как нужно решать системы неравенств с одной переменной.
Пример1: решим систему неравенств

Имеем:

Отсюда

Решениями системы являются значения x , удовлетворяющие каждому их неравенств  и
и  . Изобразив на координатной прямой множество чисел, удовлетворяющих неравенству
. Изобразив на координатной прямой множество чисел, удовлетворяющих неравенству  , и множество чисел, удовлетворяющих неравенству
, и множество чисел, удовлетворяющих неравенству , найдем, что оба неравенства верны при
, найдем, что оба неравенства верны при

Ответ : x  (3,5; 6)
(3,5; 6)
Пример2:решим систему неравенств

Имеем:

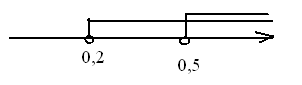
Изобразим на координатной прямой множества решений каждого из неравенств. Оба неравенства верны при  . Ответ можно записать в виде неравенства
. Ответ можно записать в виде неравенства  или в виде числового промежутка (9; +
или в виде числового промежутка (9; + ), задаваемого этим неравенством.
), задаваемого этим неравенством.
Пример3: решим систему неравенств

Имеем:

Используя координатную прямую, найдем, что множество чисел, удовлетворяющих неравенству  , и множество чисел, удовлетворяющих неравенству
, и множество чисел, удовлетворяющих неравенству  , не имеют общих элементов, т.е. их пересечение пусто. Данная система неравенств не имеет решений.
, не имеют общих элементов, т.е. их пересечение пусто. Данная система неравенств не имеет решений.
Ответ: решений нет.
4.Закрепление
А теперь перейдем к задачам из учебника. открываем учебники на странице187, №874, работаем устно.
№876(а,б)
Следующий номе это №877выполняем письменно, кто-то у доски.
остальные выполняем в тетради.
а) 



Ответ: решений нет
б) 



Ответ: x  (-
(- ; -1)
; -1)
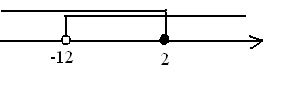
№ 880 решите систему неравенств:
а) 



Ответ: x  (-12; 2]
(-12; 2]
б) 



Ответ: решений нет.
в) 


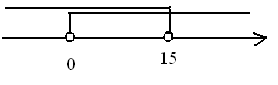
Ответ: x  (0; 15)
(0; 15)
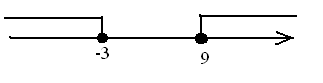
г)


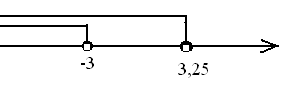
Ответ: : x  (-
(- ; -3)
; -3)
5.Подведение итогов
Итак, сегодня на уроке мы с вами познакомились с понятием системы неравенств с одной переменной, дали определение решению системы неравенств с одной переменной и разъяснили, что значит решить систему.
6.Дом/задание П.35, №876(в-е) №878
№881 решите систему неравенств
а) 



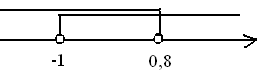
Ответ: x  (-2; 0,8)
(-2; 0,8)
б) 
 Ответ: x
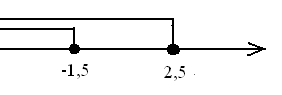
Ответ: x  (-
(- ;-1,5)
;-1,5)
в) 


Ответ: x  (0,5; +
(0,5; + ).
).








 должно удовлетворять условию
должно удовлетворять условию


 и
и  . Изобразив на координатной прямой множество чисел, удовлетворяющих неравенству
. Изобразив на координатной прямой множество чисел, удовлетворяющих неравенству 
 (3,5; 6)
(3,5; 6)

 . Ответ можно записать в виде неравенства
. Ответ можно записать в виде неравенства  ), задаваемого этим неравенством.
), задаваемого этим неравенством.

 , и множество чисел, удовлетворяющих неравенству
, и множество чисел, удовлетворяющих неравенству  , не имеют общих элементов, т.е. их пересечение пусто. Данная система неравенств не имеет решений.
, не имеют общих элементов, т.е. их пересечение пусто. Данная система неравенств не имеет решений.


























 Ответ: x
Ответ: x 


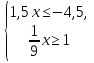
 Ответ: x
Ответ: x